
|
Claude Grasland Université Paris VII / UFR GHSS
|
Etape 1 : Etude de la densité de population des départements camerounais en 1976
1.1)
Tableau de distribution statistique
| Code | Nom | Rang | Dens. 1976 |
| C1 | BOUMBA ET NGOKO | 1 | 1.7 |
| F4 | MAYO-REY | 2 | 1.8 |
| A1 | DJEREM | 3 | 2.5 |
| A2 | FARO ET DEO | 4 | 2.9 |
| C2 | HAUT-NYONG | 5 | 3.2 |
| C4 | LOM ET DJEREM | 6 | 3.2 |
| F2 | FARO | 7 | 3.8 |
| B1 | HAUTE-SANAGA | 8 | 4.7 |
| B3 | MBAM | 9.5 | 5.0 |
| I1 | DJA ET LOBO | 9.5 | 5.0 |
| E2 | NKAM | 11.5 | 5.5 |
| C3 | KADEY | 11.5 | 5.5 |
| I3 | OCEAN | 13 | 5.9 |
| A4 | MBERE | 14 | 6.3 |
| A5 | VINA | 15 | 6.6 |
| A3 | MAYO-BANYO | 16.5 | 8.0 |
| I2 | NTEM | 16.5 | 8.0 |
| B7 | NYONG ET MFOUMO | 18 | 11.8 |
| J4 | NDIAN | 19 | 12.0 |
| E3 | SANAGA-MARITIME | 20 | 12.1 |
| F1 | BENOUE | 21 | 12.6 |
| B6 | NYONG ET KELLE | 22 | 13.6 |
| D3 | LOGONE ET CHARI | 23 | 14.5 |
| J2 | MANYU | 24 | 15.0 |
| B8 | NYONG ET SO | 25 | 21.7 |
| H6 | NOUN | 26 | 25.7 |
| B4 | MEFOU | 27 | 29.9 |
| J3 | MEME | 28.5 | 30.2 |
| G3 | MENTCHUM | 28.5 | 30.2 |
| D2 | KAELE | 30 | 37.0 |
| G2 | DONGA-MANTUNG | 31 | 40.4 |
| F3 | MAYO-LOUTI | 32 | 40.8 |
| D4 | MAYO-DANAY | 33 | 42.5 |
| H5 | NDE | 34 | 44.7 |
| D5 | MAYO-SAVA | 35 | 58.6 |
| D1 | DIAMARE | 36 | 60.4 |
| G1 | BUI | 37 | 61.7 |
| G5 | MOMO | 38 | 66.0 |
| B2 | LEKIE | 39 | 67.9 |
| D6 | MAYO-TSANAGA | 40 | 69.2 |
| E1 | MOUNGO | 41 | 74.0 |
| J1 | FAKO | 42 | 76.2 |
| G4 | MEZAM | 43 | 104.2 |
| H2 | HAUT-NKAM | 44 | 108.8 |
| H1 | BAMBOUTOS | 45 | 132.6 |
| H3 | MENOUA | 46 | 145.9 |
| H4 | MIFI | 47 | 207.1 |
| E4 | WOURI | 48 | 470.9 |
| B5 | MFOUNDI | 49 | 509.3 |
Le département le moins densément peuplé est le Boumba & Ngoko (1.7 hab./km2), le département le plus densément peuplé est le Mfoundi (509.3 hab./km2). La valeur la plus typique (la moitié des départements ont une densité inférieure, l'autre moitié une densité supérieure) est la médiane qui correspond au rang 25, c'est-à-dire au département de Nyong & So (21.7 hab. / km2).
N.B. : En cas d'ex-aequo, on remplace les rangs des ex-aequo par la moyenne de ces rangs. Ainsi les ex-aequo des rangs 5 et 6 se voient attribué le rang 5.5.
1.2) Diagramme
de distribution
| 1ere solution : graphique ordinaire |
 |
| Commentaires : On repère bien l'existence de deux valeurs exceptionnelles (les départements correspondant aux villes de Douala et Yaoundé) et une rupture vers 90 km, mais il est difficile d'analyser les variations de densité entre 0 et 100 km. |
| 2e solution : échelle logarithmique |
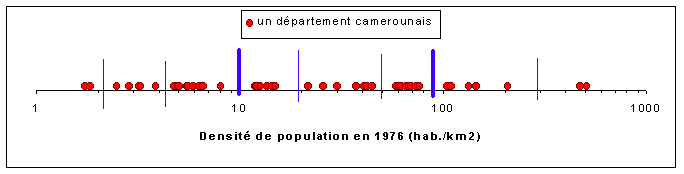 |
| Commentaires : l'utilisation d'une échelle logarithmique permet, dans le cas de la présente distribution, de beaucoup mieux repérer les zones de concentration et de dispersion des valeurs. On en déduit des ruptures majeures (vers 10 et 90) et des ruptures secondaires (vers 2, 4, 20, 50 et 300) qui pourront servir plus tard de base à la définition des limites de classes. |
| 3e solution : empilement des valeurs ex-aequo ou voisines & troncature de la distribution |
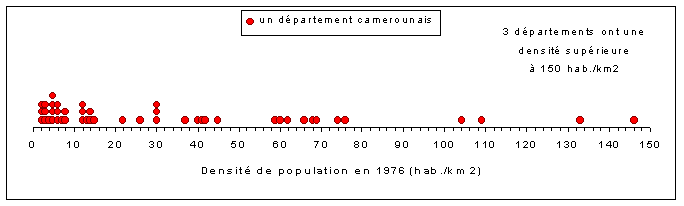 |
| Commentaires : on garde une échelle arithmétique, mais on tronque la distribution au delà de 150 et on empile les points correspondant à des départements qui ont des valeurs proches. Le graphique demeure simple et est tout à fait lisible. |
| 4e solution : la totale ! |
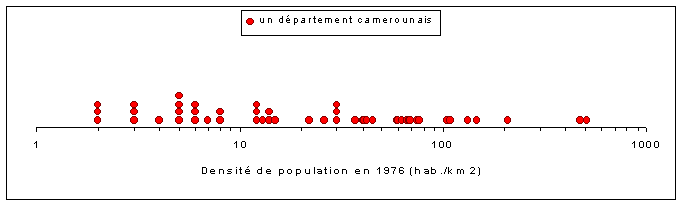 |
| Commentaires : on combine toutes les solutions précédentes pour obtenir le graphique le plus lisible, le plus efficace et le plus performant sur le plan statistique. |
1.3) Courbe
des fréquences cumulées
| 1ere solution : échelle arithmétique |
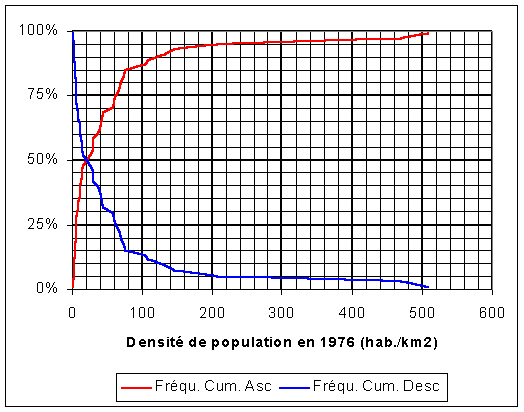 |
| Commentaires : On repère bien la concentration des valeurs de la distribution entre 0 et 30 (forte pente des courbes) et leur dispersion croissante au fur et à mesure que l'on se dirige vers les densités élevés. Tout ceci met en évidence la forte dissymétrie à gauche de la distribution (beaucoup de valeurs faibles, peu de valeurs élevées). Mais le graphique ne permet pas de bien repérer les seuils de la distribution. |
| 2e solution : échelle logarithmique |
 |
Commentaires : En utilisant une échelle logarithmique,
on peut saisir beaucoup mieux les variations de pentes qui signalent les
zones de concentration (forte pente) ou de dispersion (faible pente) des
valeurs. On peut également facilement repérer les quantiles
de la distribution et montrer par exemple que :
|
1.4)
Tableau de dénombrement - Détermination du mode de la distribution
Classes fondées sur la méthode des seuils naturels
| Classes | Effectif | Freq. Simple | Amplitude | Centre | Freq. Moy. |
| [0; 4[ | 7 | 14% | 4 | 2 | 1.75 |
| [4;10] | 10 | 20% | 6 | 7 | 1.67 |
| [10; 50[ | 17 | 35% | 40 | 30 | 0.43 |
| [50;100[ | 8 | 16% | 50 | 75 | 0.16 |
| [100;300[ | 5 | 10% | 200 | 200 | 0.03 |
| [300 ; 510[ | 2 | 4% | 210 | 405 | 0.01 |
| Total | 49 | 100% | 510 | 255 | 0.10 |
Classes fondées sur la méthode des amplitudes égales
| Classes | Effectif | Freq. Simple | Amplitude | Centre | Freq. Moy. |
| [0; 85[ | 42 | 86% | 85 | 42.5 | 0.49 |
| [85;170] | 4 | 8% | 85 | 127.5 | 0.05 |
| [170; 255[ | 1 | 2% | 85 | 212.5 | 0.01 |
| [255;340[ | 0 | 0% | 85 | 297.5 | 0.00 |
| [340;425[ | 0 | 0% | 85 | 382.5 | 0.00 |
| [425 ; 510[ | 2 | 4% | 85 | 467.5 | 0.02 |
| Total | 49 | 100% | 510 | 255 | 0.10 |
Classes fondées sur la méthode des amplitudes égales
| Classes | Effectif | Freq. Simple | Amplitude | Centre | Freq. Moy. |
| [0; 4] | 8 | 16% | 5 | 2.5 | 1.60 |
| [5;10] | 9 | 18% | 5 | 7.5 | 1.80 |
| [10; 22[ | 8 | 16% | 12 | 16 | 0.67 |
| [22;43[ | 8 | 16% | 21 | 32.5 | 0.38 |
| [43;75[ | 8 | 16% | 32 | 59 | 0.25 |
| [75 ; 510[ | 8 | 16% | 435 | 292.5 | 0.02 |
| Total | 49 | 100% | 510 | 255 | 0.10 |
On remarque combien la valeur du mode peut fluctuer (2, 7.5,
42.5) selon le choix des classes.
1.5) Construction d'un histogramme
Franchement, EXCEL ne sait pas faire les histogrammes, sauf dans le cas particulier des classes d'amplitudes égales. Encore faut-il le forcer à rendre les classes jointives en allant dans les options du graphique.
Sinon, il reste le "bidouillage" mais je renonce à expliquer la méthode que j'emploie : reportez-vous à la feuille EXCEL 1-5 pour voir si vous comprenez comment j'ai fait. Notez-bien que le remplissage des histogrammes et la légende ont été réalisés sous PAINT.
Si un petit génie de Visual BASIC peut construire un module générant
des histogrammes... je lui ajoute sans hésiter une note de 20/20
aux autres notes de contrôle continu !
| Classes fondées sur la méthode des seuils naturels |
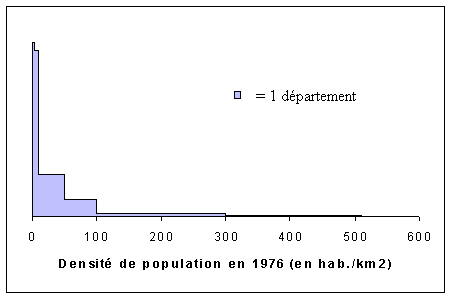 |
| Classes fondées sur la méthode des amplitudes égales |
 |
| Classes fondées sur la méthode des effectifs égaux |
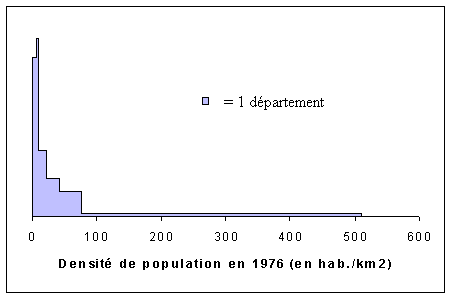 |
![]()