
INTRODUCTION
Une analyse spatiale multiscalaire se heurte d'emblée à des problèmes de disponibilité des données, mais ces derniers peuvent être surmontés si l'on accepte de limiter l'analyse à un nombre réduit d'indicateurs. Elle pose en outre des problèmes théoriques et méthodologiques liés au fait que l'on ne mesure plus la valeur d'un indicateur à l'intérieur d'un territoire connu au contours biens délimités (e.g. population de la France) mais en tous points de l'espace à l'intérieur d'un voisinage fondé sur une distance autour des points d'observation retenus (e.g. population contenue dans un rayon de 250 km, de 3 heures, etc.).
Pour illustrer l'intérêt mais aussi la difficulté d'une telle approche, nous allons partir d'un exemple relativement simple, celui de la comparaison des niveaux de population et de richesse en trois points précis de la surface de la Terre : Saint-Dié des Vosges (France), Calcutta (Inde) et Sydney (Australie).
Pour donner une finalité à l'exercice, on peut imaginer la fiction suivante : une entreprise multinationale souhaite implanter une très grosse unité de production sur l'un de ces trois sites et vise à disposer simultanément d'un vaste marché de main d'oeuvre (concentration spatiale de population autour du lieu d'implantation) et d'un vaste marche de consommation (concentration spatiale de la population mais aussi et surtout de la richesse autour du lieu d'implantation). On suppose que cette entreprise est indifférente aux frontières politiques (elle est prête à importer sa main d'oeuvre ou à exporter ses produits à l'extérieur des limites de l'Etat où sera choisi le lieu d'implantation), de sorte que des renseignements tels que la population en habitant ou la richesse en dollars de l'état dans lequel les trois villes sont localisées ne lui est d'aucune utilité particulière (on remarquera d'ailleurs que les trois villes sélectionnées sont excentrées par rapport au centre de gravité de la population, de la richesse ou de la superficie des Etats auxquels elles appartiennent respectivement). Pour simplifier le problème, on supposera que les coûts de mise en relation de toute nature (déplacements de main d'oeuvre, transport des produits finis, circulation de l'information ) sont simplement proportionnels à la distance à vol d'oiseau séparant le lieu d'implantation des foyers de richesse ou de main d'oeuvre nécessaires à son fonctionnement.
La réalisation d'une étude "sans frontière"
conduit d'un point de vue conceptuelle à remplacer la notion d'appartenance
territoriale (localisation à l'intérieur d'une maille)
par la notion d'accessibilité spatiale (distance d'un lieu
à un ensemble de ressources localisées en d'autres lieux).
Mathématiquement, ceci revient à étudier les interactions
entre les lieux dans l'espace à l'aide d'une métrique
continue (probabilité d'interaction mesurée par une fonction
décroissante de la distance valant 1 pour une distance nulle et
0 pour une distance infinie) plutôt qu'à l'aide d'une métrique
discrète (probabilité d'interaction mesurée par
un indicateur prenant la valeur 1 si deux lieux sont localisés dans
la même maille territoriale et 0 dans le cas contraire).
Définir l'accessibilité spatiale d'un lieu
consiste à mesurer l'éloignement de ce lieu à
une ressource distribuée dans l'espace autour de celui-ci.
Toute étude d'accessibilité suppose donc que l'on ait bien
précisé :
Indépendamment même des choix précédents, il est possible de proposer des mesures très différentes de l'accessibilité d'un lieu, selon les hypothéses faites sur les objectifs des acteurs qui souhaitent accéder aux ressources distribuées dans l'espace. Certains acteurs pourront par exemple privilégier une accessibilité à courte portée (intérêt exclusif pour les ressources situées à courte distance) alors que d'autres privilégieront des accessibilités à longue portée (intérêt pour des ressources situées éventuellement à longue ou très longue distance). Or, un lieu peut très bien avoir une bonne accessibilité à courte portée et une médiocre accessibilité à longue portée (e.g. une ville située au milieu d'un désert) tandis qu'un autre pourra présenter les caractéristiques inverses (e.g. une zone rurale peu dense mais entourée par des zones de concentration urbaine).
Tenter de résumer l'accessibilité d'un lieu à l'aide
d'un indicateur unique d'accessibilité (e.g. distance
moyenne à l'ensemble des ressources) apparaît donc le plus
souvent comme une tentative assez vaine et fortement simplificatrice de
la réalité. Il est beaucoup plus intéressant, comme
nous allons le montrer maintenant, de mesurer l'accessibilité d'un
lieu à l'aide d'une courbe cumulative de la quantité de
ressources en fonction de la distance à ce lieu.
Pour fixer les idées, nous allons partir d'un exemple très
simple, celui de la construction de la courbe d'accessibilité
démographique mondiale de la ville de Saint-Dié-des-Vosges,
c'est-à-dire étudier la distribution des distances entre
Saint-Dié-des-Vosges et l'ensembles des 5.3 milliards d'habitants
de la terre en 1990.
A moins de disposer d'une information très précise sur la répartition des habitants à l'intérieur de Saint-Dié, on ne peut mesurer l'accessibilité qu'à partir d'une certaine distance depuis le centre de la ville de Saint-Dié. Sachant que cette dernière comptait en 1990 environ 22500 habitants répartis sur une surface de 47 km2, on peut estimer qu'il y a un peu plus 20 000 habitants dans un rayon de 4 km autour de la mairie de Saint-Dié (on assimile pour cela la commune de Saint-Dié à un cercle de rayon 3.9 km). Ce calcul est évidemment assez imprécis, mais il nous fournit une première mesure de la quantité de ressource en fonction de la distance, un premier point à la courbe d'accessibilité que nous cherchons à établir :
Tableau 1 : Construction de la courbe d'accessibilité de Saint-Dié (1ere étape)
| Distance à Saint-Dié | Population cumulée |
| 4 km | 20 000 h. |
On peut ensuite utiliser la distribution des populations par commune
fournie par l'INSEE pour déterminer la quantité de population
située à moins de 10 km, 20 km, 30 km ou 50 km autour de
Saint-Dié. Là encore, il faut tenir compte d'une certaine
imprécision dans le calcul puisque la population de chaque commune
est assimilée à un point unique alors qu'en réalité
elle est distribuée sur une surface. Les quantités de population
obtenues par cette méthode sont donc des approximations de la quantité
de population réellement située à l'intérieur
des cercles considérés. Cette approximation devient toutefois
de moins en moins gênante au fur et à mesure que l'on accroît
la portée des cercles puisque beaucoup de communes sont alors concernées
et que l'on peut supposer que les erreurs tendent à se compenser.
| Figure 1 : Distribution de la population des communes situées autour de Saint-Dié-des-Vosges en 1990 |
 |
A partir des informations contenues sur la Figure 1, on peut maintenant compléter notre courbe cumulative en lui ajoutant les points qui correspondent à la population cumulée dans des rayons de plus en plus importants (10, 20, 30, 40, 50 km) autour de Saint-Dié-des-Vosges (Tableau 2).
Tableau 2 : Construction de la courbe d'accessibilité de Saint-Dié (2e étape)
| Distance à Saint-Dié | Population cumulée |
| ... | ... |
| 10 km | 40 000 h. |
| 20 km | 96 000 h |
| 30 km | 187 000 h |
| 40 km | 470 000 h. |
| 50 km | 750 000 h. |
La population cumulée augmente évidemment plus vite que la distance puisque les superficies qui sont ajoutées à chaque étape du calcul sont de plus en plus importantes. Si la population était répartie de façon homogène autour de Saint-Dié, le cumul de la population augmenterait à une constante près en fonction du carré de la distance. Dans l'exemple étudié, on pourrait montrer que l'accroissement de population n'est pas régulier car certaines couronnes sont plus "riches" en population que d'autres autour de Saint-Dié. La couronne située entre 30 et 40 km correspond à un saut particulièrement brutal de la courbe d'accessibilité puisque c'est dans cette tranche de distance que les grandes métropoles péri-vosgiennes (Colmar, Epinal) entrent dans le rayon d'accessibilité de Saint-Dié. L'augmentation demeure également forte entre 40 et 50 km, en raison de l'arrivée des fortes densités des communes de la plaine d'Alsace à l'Est (de Guebwiller à Molsheim) et de la vallée de la Moselle au sud.
Ce début de courbe prometteur ne peut cependant pas être
poursuivi avec la même base de données (communes françaises)
au delà de 50 kilomètres, car on serait alors amené
à négliger l'influence des populations allemandes et suisses
sur l'accessibilité démographique de Saint-Dié. Il
faut donc mobiliser une nouvelle source d'information, la population des
régions européennes, pour continuer à tracer la courbe
d'accessibilité pour des rayons plus grands.
| Figure 2 : Distribution de la population des régions européennes situées autour de Saint-Dié-des-Vosges vers 1990 |
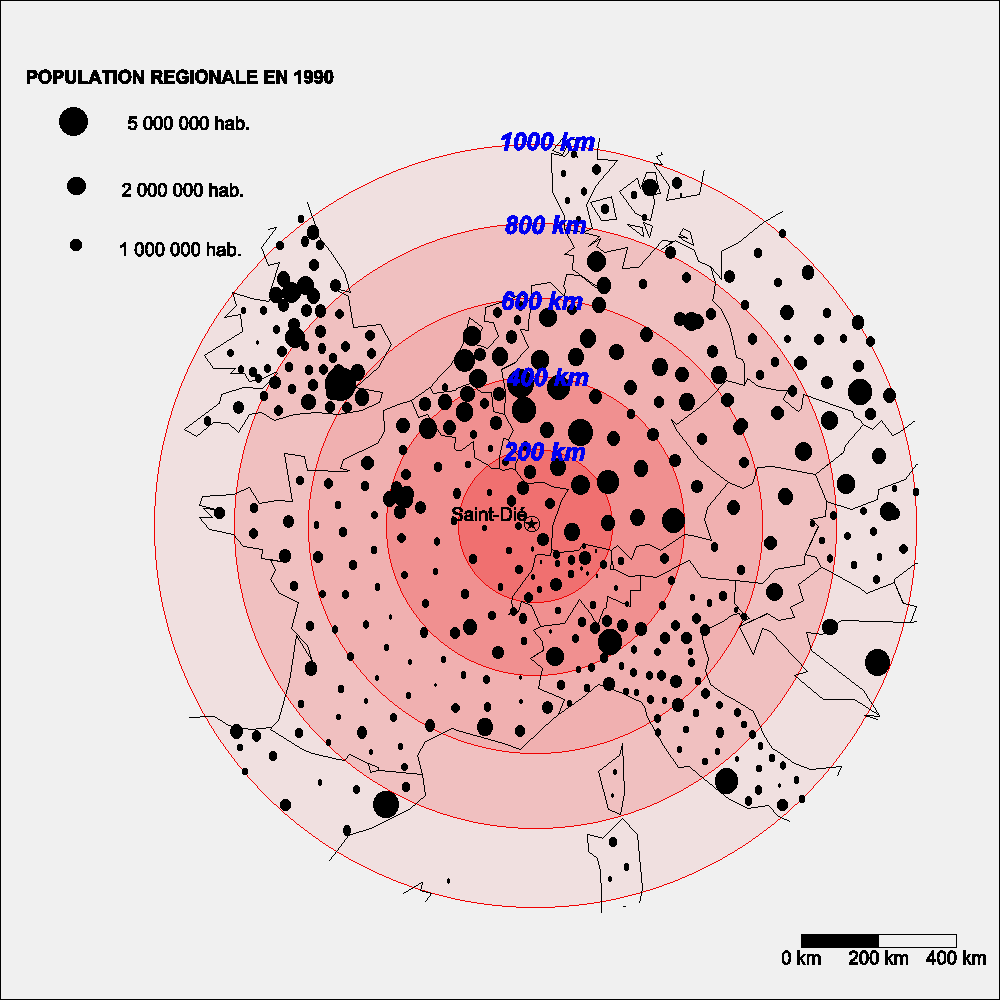 |
L'information est maintenant beaucoup moins précise que précédemment
(régions européennes d'une taille équivalente à
celle des départements français), mais comme les cercles
où s'opérent les comptages sont également bien plus
étendus (200 à 1000 km), cette imprécision n'est guère
gênante et les ordres de grandeur obtenus demeurent valable. On pourrait
évidemment recourir à des bases de données plus précises
(communes ou districts européens) si l'on souhaitait affiner le
résultat correspondant à la troisième étape
du calcul :
Tableau 3 : Construction de la courbe d'accessibilité de Saint-Dié (3e étape)
| Distance à Saint-Dié | Population cumulée |
| ... | ... |
| 200 km | 21 000 000 h. |
| 400 km | 104 000 000 h. |
| 600 km | 179 000 000 h. |
| 800 km | 258 000 000 h. |
| 1000 km | 330 000 000 h. |
On remarquera le très fort saut de la courbe lorsque l'on passe d'un rayon de 200 km à un rayon de 400 km (multiplication par 5 de la population) alors que pour les portées supérieures les accroissements sont beaucoup plus modérés (inférieurs à un doublement). C'est en effet entre 200 et 400 km autour de Saint-Dié que se localisent les plus grandes masses de peuplement ouest-européennes (Rhur, Paris, Milan, Münich, ...). A contrario, le cumul de population est ralenti au delà de 400 km par l'apparition d'étendues maritimes de plus en plus vastes qui réduisent mécaniquement la quantité de population cumulable. On pourrait contrôler cet effet en cumulant non seulement les populations mais aussi les superficies de terres émergées autour de Saint-Dié : on pourrait alors effectuer le rapport des deux et calculer non plus la population mais la densité de population dans des rayons de taille variable autour de Saint-Dié.
Pour achever le calcul de la courbe d'accessibilité à
l'ensemble de la population mondiale, il faut recourir à une dernière
base de donnée indiquant la distribution de tous les habitants de
la terre par degrés de latitude et de longitude (base UNEP-GRID)
et substituer à la distance euclidienne utilisée jusqu'ici
la distance orthodromique qui est la longueur de l'arc de plus court
chemin reliant deux points à la surface d'une sphère.
| Figure 3 : Distribution de la population mondiale par degrés de latitude et de longitude vers 1990 |
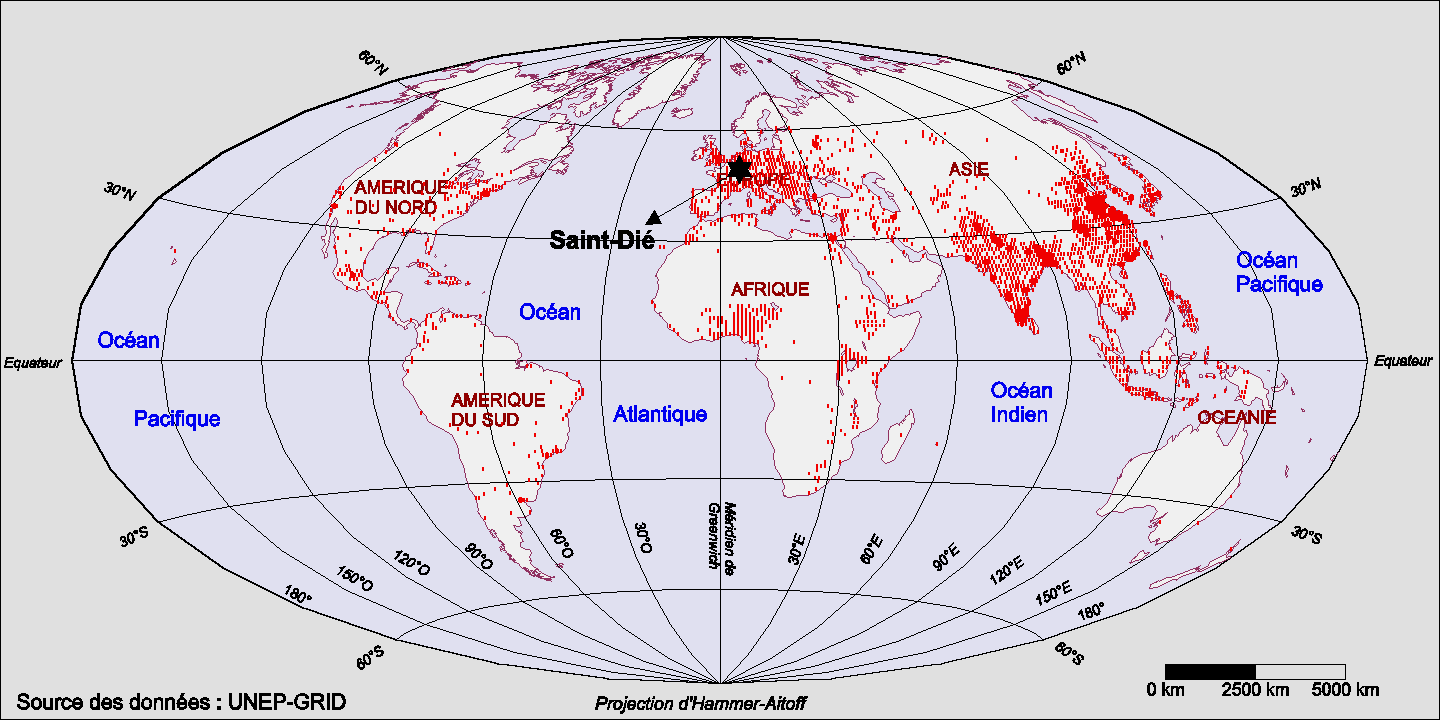 |
Bien que les trapézes définis par la grille de 1°
de latitude et de longitude correspondent à des surfaces considérables
(carré de 110 kilomètres de côté à l'Equateur),
ils fournissent une précision tout à fait suffisante pour
calculer la population dans des rayons de plusieurs milliers de kilomètre
autour de Saint-Dié.
Tableau 4 : Construction de la courbe d'accessibilité de Saint-Dié (4e étape)
| Distance à Saint-Dié | Population cumulée |
| ... | ... |
| 5 000 km | 1 300 000 000 h. |
| 10 000 km | 4 910 000 000 h. |
| 15 000 km | 5 270 000 000 h. |
| 20 000 km | 5 290 000 000 h. |
On constate ainsi que 1.3 milliards d'habitants sont localisés
à moins de 5000 kilomètre à vol d'oiseau autour de
Saint-Dié et que 4.9 milliards d'habitants (soit 92 % de la population)
se concentrent dans un hémisphère dont le pôle serait
Saint-Dié-des-Vosges tandis que seuls 380 millions d'habitants se
localisent dans l'hémisphère opposé (c'est-à-dire
à une distance de Saint-Dié supérieure à 10
000 kilomètres).
| Figure 4 : Distribution de la population mondiale en fonction de la distance à Saint-Dié (0 à 20 000 kilomètres) |
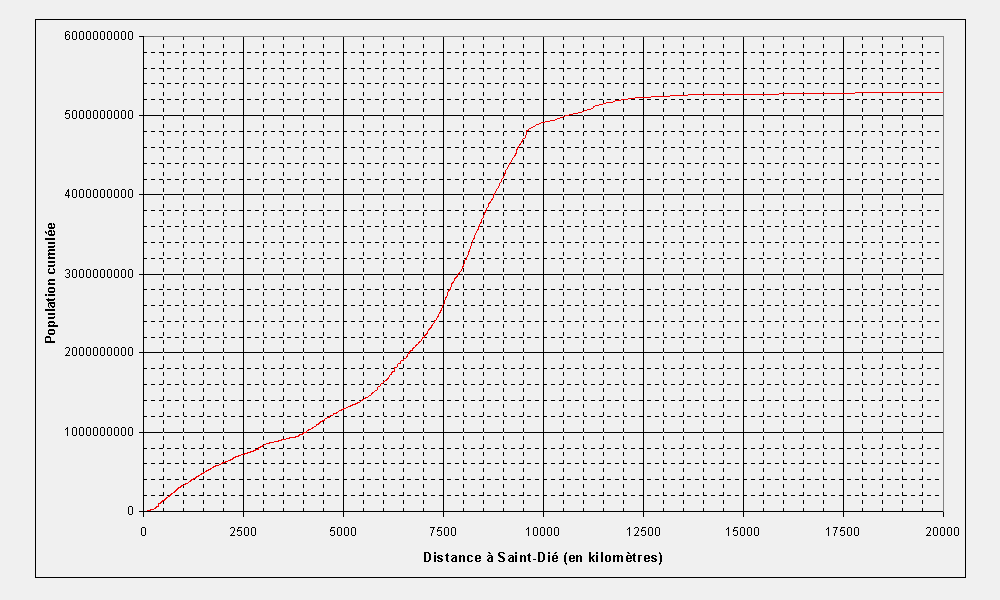 |
Cette courbes autorisent une double lecture de l'accessibilité
de Saint-Dié, selon que l'on part d'une abcisse pour trouver
une ordonnée ou selon que l'on part d'une ordonnée pour trouver
l'abcisse correspondante.
Cette première courbe présente toutefois un intérêt
très relatif puisque l'on peut supposer qu'il existe peu d'acteurs
économiques ou politiques à Saint-Dié susceptibles
de nouer des relations avec la terre entière (même s'il existe
un festival mondial de géographie qui se tient tous les ans à
Saint-Dié). Il semble donc plus intéressant d'effectuer également
un zoom sur la partie de la courbe décrivant les accessibilités
à moyenne distance (0 à 2000 kilomètres) voire à
courte distance (0 à 50 kilomètres).
| Figure 5 : Distribution de la population mondiale en fonction de la distance à Saint-Dié (0 à 2000 kilomètres) |
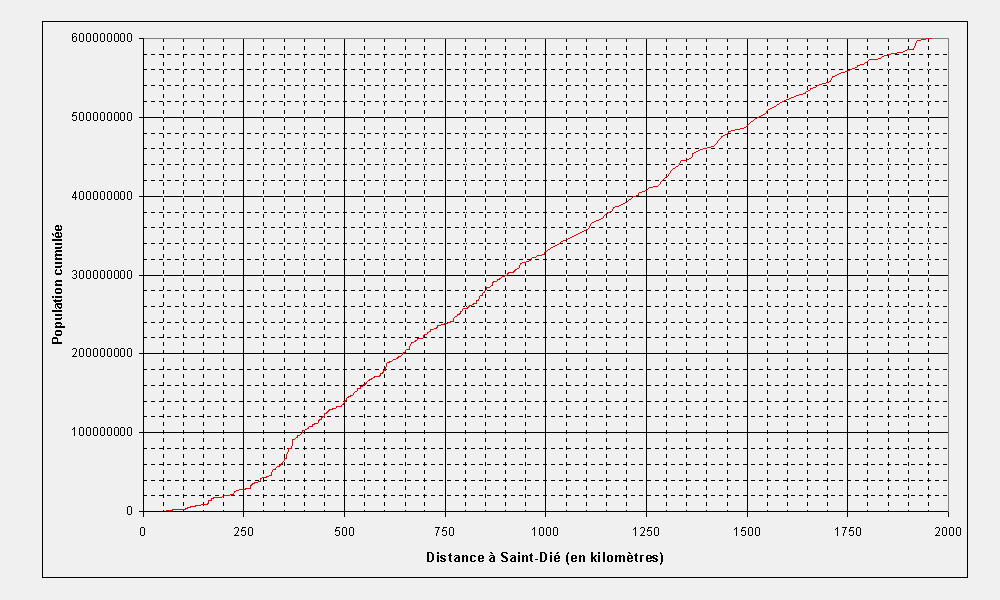 |
Si l'on excepte un brusque saut de la courbe cumulative entre 300 et
400 kilomètres (influence de Paris et des grandes métropoles
rhénanes), la courbe cumulative de la population en fonction de
la distance à Saint-Dié apparaît remarquablement régulière
entre 400 et 2000 kilomètres et forme pratiquement une droite. Nous
avons vu précédemment qu'elle aurait du former une parabole
si la population était répartie de façon homogène
(densité de population constante) autour de Saint-Dié, mais
ce n'est pas le cas pour deux raisons : (1) la part des étendues
maritimes devient de plus en plus importante au fur et à mesure
que l'on s'éloigne de Saint-Dié et (2) les densités
de population des terres émergées sont également de
plus en plus faibles au fur et à mesure que l'on s'éloigne
de la zone rhénane où se trouve Saint-Dié.
| Figure 6 : Distribution de la population mondiale en fonction de la distance à Saint-Dié (0 à 200 kilomètres) |
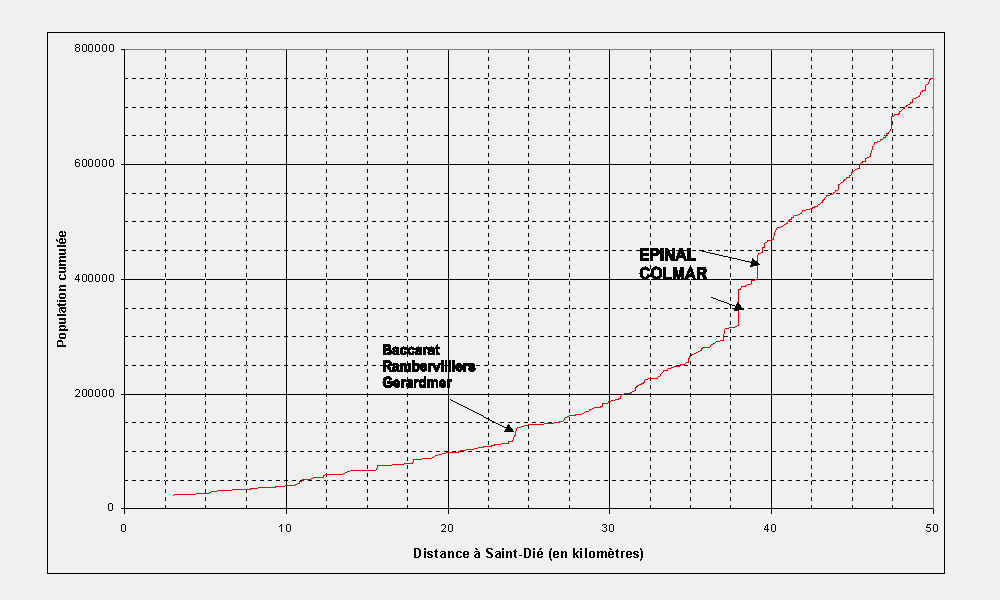 |
A très courte distance (0 à 50 kilomètres) la courbe présente un aspect plus heurté et laisse nettement apparaître deux "marches d'escalier", l'une vers 25 kilomètres (distance de Saint-Dié aux villes de niveau équivalents) et l'autre vers 4O kilomètres (distance de Saint-Dié aux villes de niveau supérieurs). Ces irrégularités sont en fait très révélatrice des règles d'espacement régulier des villes (théorie de Christaller) que l'on peut observer dans cette partie du territoire français. La remontée générale de la pente de la courbe au delà de 40 kilomètres signale par ailleurs la sortie du massif vosgien (dont Saint-Dié constitue approximativement le centre) et l'apparition des zones plus densément peuplées d'Alsace et de Lorraine sur les pourtours de ce massif.
On le voit, les courbes d'accessibilité apportent une information
très riche sur la position relative des lieux et peuvent se prêter
à de très nombreuses utilisations. En effet, nous n'avons
envisagé ici que le cas de l'étude de l'accessibilité
d'un lieu isolé (Saint-Dié), mais il est beaucoup plus instructifs
de comparer les courbes d'accessibilités de plusieurs lieux ou d'un
même lieu pour différentes ressources, pour différentes
distances, etc.
Pour chacune de ces localisations, le CD-Rom 6 milliards d'hommes
nous permet (après avoir repéré leurs coordonnées
de latitude et de longitude dans un Atlas) de visualiser les courbes
cumulatives d'accessibilité par rapport à la population et
la richesse mondiale (Figure 7).
On peut ensuite extraire de ces graphiques un certain nombre de paramètres caractéristiques correspondant à des portées croissantes (250, 500, 1000, 2000, 5000 et 10000 km). Pour convertir les pourcentage du total de la population ou de la richesse mondiale en valeurs brutes, il suffit de connaître le total de la population mondiale en 1990 (5290 millions d'habitants) ainsi que celui de la richesse mondiale à la même date (27450 milliards de dollars). On obtient ainsi pour chacun des trois lieux étudiés un tableau résumant les caractéristiques de son accessibilité pour les mêmes distances et l'on peut entreprendre différentes comparaisons de leurs situations respectives à chacune des portées (Tableau 5). .
Tableau 5 : Paramètres caractéristiques de l'accessibilité démographique et économique de trois points de la surface du globe.
| Saint-Dié | ||||||
| Distance | Population cumulée | Richesse cumulée | Richesse par habitants | |||
| millions hab. | % | milliards $ | % | dollars/hab | indice 100 | |
| 250 km |
29
|
0.5%
|
910
|
3.3%
|
31379
|
603
|
| 500 km |
128
|
2.4%
|
3540
|
12.9%
|
27656
|
531
|
| 1000 km |
328
|
6.2%
|
7170
|
26.0%
|
21860
|
420
|
| 2000 km |
616
|
11.6%
|
9100
|
33.0%
|
14773
|
284
|
| 5000 km |
1299
|
24.6%
|
10500
|
38.1%
|
8083
|
155
|
| 10000 km |
4917
|
92.9%
|
26250
|
95.3%
|
5339
|
103
|
| 20000 km |
5291
|
100.0%
|
27540
|
100.0%
|
5205
|
100
|
| Calcutta | ||||||
| Distance | Population cumulée | Richesse cumulée | Richesse par habitants | |||
| millions hab. | % | milliards $ | % | dollars/hab | indice 100 | |
| 250 km |
60
|
1.1%
|
20
|
0.1%
|
333
|
6
|
| 500 km |
215
|
4.1%
|
70
|
0.3%
|
326
|
6
|
| 1000 km |
466
|
8.8%
|
210
|
0.8%
|
451
|
9
|
| 2000 km |
1309
|
24.7%
|
710
|
2.6%
|
542
|
10
|
| 5000 km |
3093
|
58.5%
|
5870
|
21.3%
|
1898
|
36
|
| 10000 km |
4533
|
85.7%
|
18860
|
68.5%
|
4161
|
80
|
| 20000 km |
5291
|
100.0%
|
27540
|
100.0%
|
5205
|
100
|
| Sydney | ||||||
| Distance | Population cumulée | Richesse cumulée | Richesse par habitants | |||
| millions hab. | % | milliards $ | % | dollars/hab | indice 100 | |
| 250 km |
3
|
0.1%
|
50
|
0.2%
|
20074
|
386
|
| 500 km |
4
|
0.1%
|
80
|
0.3%
|
20049
|
385
|
| 1000 km |
10
|
0.2%
|
210
|
0.8%
|
20096
|
386
|
| 2000 km |
14
|
0.3%
|
290
|
1.0%
|
20000
|
384
|
| 5000 km |
104
|
2.0%
|
490
|
1.8%
|
4692
|
90
|
| 10000 km |
2493
|
47.1%
|
8010
|
29.1%
|
3213
|
62
|
| 20000 km |
5291
|
100.0%
|
27540
|
100.0%
|
5205
|
100
|
La réponse la plus communément utilisée consiste
à calculer l'accessibilité moyenne, c'est-à-dire
la distance des lieux à l'ensemble des ressources considérée.
On pondérera donc chaque point de la surface de la terre par sa
population ou sa richesse et l'on effectuera la moyenne pondérée
des distances pour chacun des lieux que l'on veut comparer. Les résultats
sont présentés dans le Tableau 6.
Tableau 6 : Accessibilité démographique et accessibilité économique moyennes de trois points de la surface de la terre
| Point de la surface terrestre | Distance moyenne à l'ensemble de la population mondiale vers 1990 | Distance moyenne à l'ensemble de la richesse mondiale vers 1990 |
| Saint-Dié | 6800 km | 5700 km |
| Calcutta | 5400 km | 8300 km |
| Sydney | 11200 km | 13100 km |
On constate que la meilleure accessibilité démographique
est obtenue par Calcutta, proche des deux plus grands foyers de peuplement
du monde (Inde et Chine) et dont la distance moyenne à l'ensemble
des habitants de la Terre est environ de 5400 kilomètres. Les accessibilités
démographiques moyennes de Saint-Dié (6800 kilomètres)
et surtout de Sydney (11200 km) sont nettement plus faibles.
Mais si l'on considère la proximité de ces lieux non
plus par rapport à l'ensemble des habitants mais par rapport à
l'ensemble des richesses mondiales (mesurées par le PNB), les conclusions
sont tout à fait différentes. C'est en effet Saint-Dié
qui apparaît alors le lieu le plus accessibles (5400 kilomètre)
puisque situé au coeur de la plus grande masse économique
mondiale (Europe) et à égale distance des deux autres grands
foyers de richesse mondiaux (Amérique du Nord et Japon). La situation
de Calcutta apparaît désormais nettement moins bonne (8300
km) mais toujours supérieure à celle de Sydney (13100 km)
qui demeure une périphérie quel que soit le critère
de pondération adopté.
Le défaut de l'accessibilité moyenne est toutefois de confondre l'ensemble des portées possibles et d'accorder implicitement le même poids aux ressources proches et éloignées. L'accessibilité moyenne n'intéresse en définitive que les acteurs mondiaux, c'est-à-dire ceux qui sont disposés à entrer en contact avec l'ensemble de la planète (firmes multinationales, superpuissances, ...) et elle n'aurait guère d'intérêt pour des acteurs économiques, politiques ou sociaux dont les relations se limitent à des distances plus courtes. Les courbes cumulatives répondet beaucoup mieux au besoin de tels acteurs puisqu'elles permettent de fixer une borne supérieure aux distances qu'un acteur peut accepter de franchir et lui indiquent le cumul correspondant de population ou de richesse.
Si par exemple une firme commercial possède un rayon d'action maximum de 1000 kilomètres et si elle souhaite implanter une filiale dans l'une des trois villes considérées, elle peut facilement déterminer le volume démographique de son bassin de main d'oeuvre (nombre d'habitants situés à moins de 1000 kilomètres) et le volume économique de son marché potentiel (quantité de richesse localisée à moins de 1000 kilomètres). Elle constatera ainsi qu'il y a 466 millions d'habitants dans un rayon de 1000 kilomètres autour de Calcutta contre 328 millions d'habitants dans le même rayon autour de Saint-Dié et seulement 10 millions d'habitants dans un rayon de 1000 kilomètres autour de Sydney. D'un point de vue économique, la quantité de richesse localisée dans un rayon de 1000 kilomètres autour de Saint-Dié est de 7170 milliards de dollars alors qu'elle n'est que d'environ 210 milliards de dollars autour de Calcutta ou de Sydney. Le fait que le potentiel de richesse de ces deux villes soit le même dans un rayon de 1000 kilomètres s'explique par le fait que le PNB par habitants des habitants d'Australie ou de Nouvelle-Zélande est pratiquement 50 fois plus élevé que celui des habitants d'Inde et du Bangladesh !
Le classement des lieux en termes d'accessibilité varie donc
fortement selon le critère de pondération adopté (population
et richesse) mais aussi selon la portée de relation maximale utilisée
par un acteur. Ainsi, nous avons vu que la population cumulée dans
un rayon de 1000 kilomètres était plus forte autour de Calcutta
que de Sydney, mais la conclusion serait différente si l'on avait
retenue une portée plus grande. Ainsi, un hémisphère
centré sur Saint-Dié (portée 10 000 km) regrouperait
93% de la population mondiale alors que le même hémisphère
centré sur Calcutta n'en regrouperait que 86%. Calcutta est en effet
beaucoup plus éloigné que Saint-Dié du continent américain,
ce qui explique que son accessibilité soit plus faible lorsque l'on
considère de très grandes portées de relation.
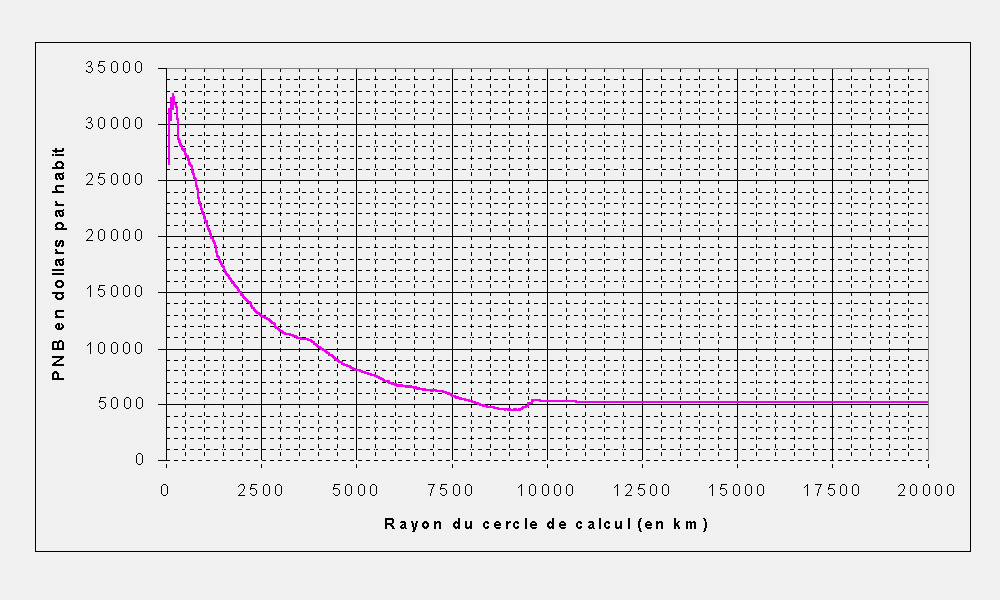
Dans le cas de Saint-Dié, par exemple, on constate que la courbe cumulative de la richesse croit beaucoup plus vite que celle de la population lorsque la distance augmente. Cela signifie que la richesse par habitant autour de Saint-Dié est très supérieure à la moyenne mondiale et que, pour la plupart des portées, on trouvera une proportion plus élevée de la richesse mondiale que de la population mondiale autour de Saint-Dié. Ainsi, dans un rayon de 1000 kilomètres autour de Saint-Dié on trouve 616 millions d'habitants (11.6% de la population mondiale) et 9100 milliards de dollars (33% de la richesse mondiale), ce qui signifie que le PNB par habitant dans le cercle de rayon 2000 kilomètres centré sur Saint-Dié est environ de 15000 dollars par habitants soit près de trois fois plus que la moyenne mondiale (5200 dollars par habitants). En effectuant le rapport des deux courbes de richesse cumulée et de population cumulée en fonction de la distance, on peut établir une courbe de la richesse par habitant dans des rayons de plus en plus grands autour de Saint-Dié (Figure 8.1). L'allure généralement décroissante de la courbe indique que, d'une manière générale, plus on s'éloigne de Saint-Dié, plus le PNB par habitant diminue, ce qui indique que Saint-Dié est situé dans la zone de richesse maximale à l'échelle mondiale.
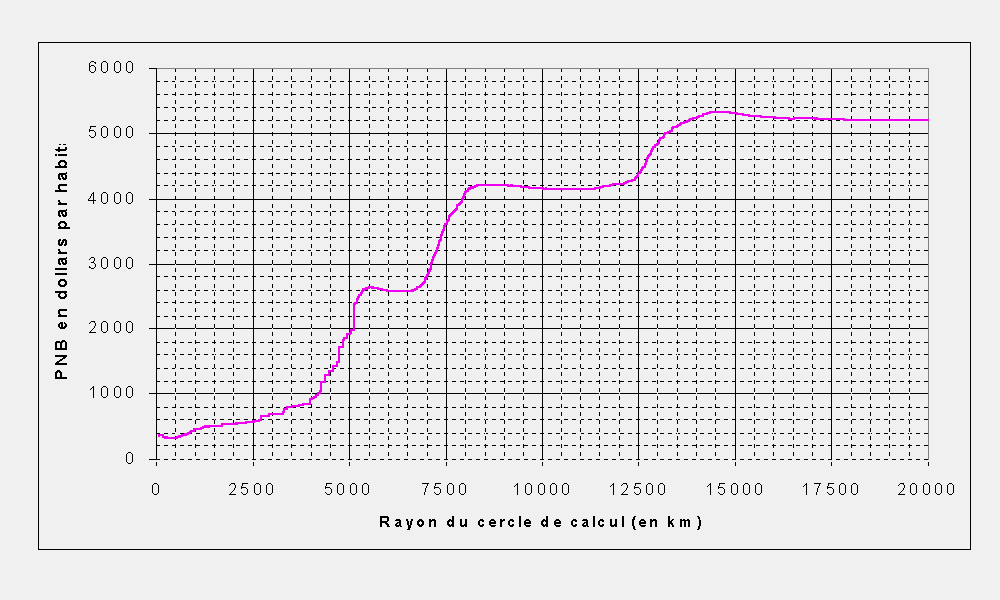
Dans le cas de Calcutta, la conclusion serait rigoureusement inverse. En effet, comme on peut le voir sur la Figure 8.2, le PNB par habitant augmente au fur et à mesure que l'on augmente la distance à Calcutta. La courbe présente trois "sauts" caractéristiques qui correspondent aux inclusions successives des trois grands foyers de richesse mondiaux dans le périmètre du cercle centré sur Calcutta : inclusion du Japon vers 5000 km, de l'Europe de l'Ouest vers 8000 km et de l'Amérique du Nord vers 14000 km. Malgré ces sauts, l'allure presque rigoureusement ascendante de la courbe du PNB par habitant indique que Calcutta est situé dans la zone de pauvreté maximale à l'échelle mondiale.
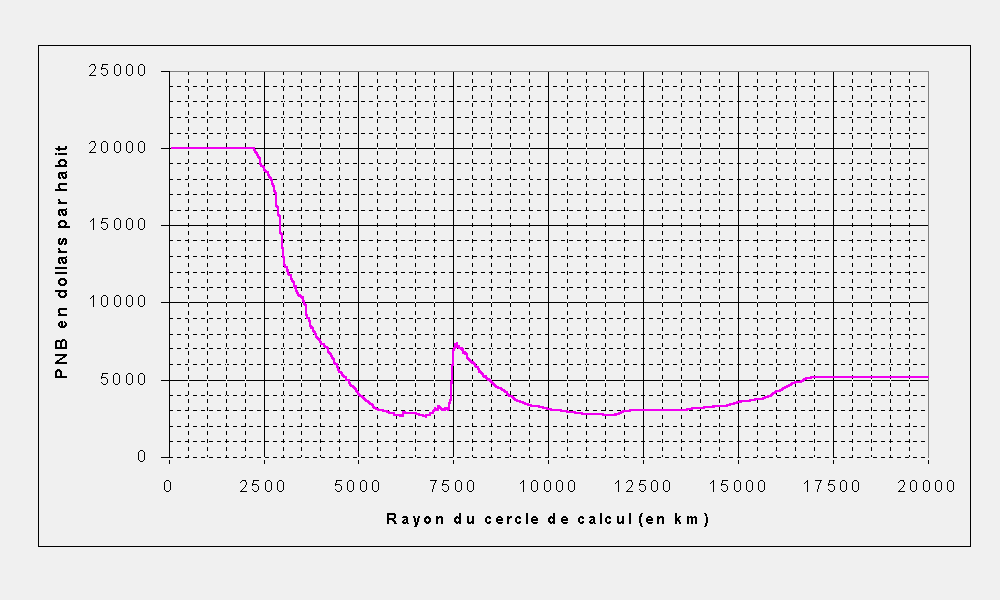
Dans le cas de Sydney, la situation est un peu plus compliquée
puisque la courbe présenté sur la Figure 8.3 est globalement
décroissante mais présente toute une série d'oscillations
positives et négatives. Ces oscillations sont en fait la marque
de l'existence de zones alternativement riches et pauvres au fur et à
mesure que l'on accroît la distance à Sydney. Ainsi, jusque
vers 2000 km, le PNB par habitant est stable et très élevé
puisque le cercle centré sur Sydney n'englobe alors que des régions
très développées d'Australie et de Nouvelle-Zélande.
La décroissance rapide entre 2500 et 5000 kilomètres signale
la traversée des régions globalement très pauvres
et très peuplées d'Asie du Sud-Est, tandis que la brutale
remontée vers 7500 kilomètres correspond à l'englobement
dans le cercle centré sur Sydney du foyer économique japonais
et de ses satellites.Si l'on ne retient que les premières oscillations
de la courbe, on peut dire que Sydney correspond à un pic de
richesse isolé à l'intérieur d'une partie relativement
pauvre de la planète.
| Figure 8 : PNB par habitant pour différents rayons autour de trois points de la terre |
| Figure 8.1 : Saint-Dié |
 |
| Figure 8.2 : Calcuta |
 |
| Figure 8.3 : Sydney |
 |
CONCLUSION
Bien que très simple dans son principe (un peu moins dans sa réalisation), l'exercice mené sur les trois villes de Sydney, Calcutta et Saint-Dié permet de bien comprendre la complexité d'un problème apparemment aussi simple que le choix d'une localisation optimale par rapport à la population et la richesse.
Il apparaît en effet d'emblée que le problème est insoluble tant que l'on n'a pas fixé la portée spatiale des interactions qui doivent être analysées ou, dans le cas présent, la portée maximale de relation envisagée par la firme pour constituer son bassin de main d'oeuvre et son bassin de chalandise.
Il apparaît également que la réponse
à la question posée dépend également du choix
des critères retenus et de leur pondération. Si l'on fixe
par exemple la portée des interactions à 2000 kilomètres,
on constate que la localisation optimale correspond :