GO152 : Introduction à la statistique et à la cartographie en géographie
Jean-Christophe François & Claude Grasland
Université Paris VII / UFR GHSS - Deug de Géographie- 1ere année / Année 1999-2000 / 2^nd Semestre

STAT.3 : LES VALEURS CENTRALES

PLAN

EXEMPLES

Retour au menu général

PLAN DU CHAPITRE STAT.3

1. LE CALCUL DES VALEURS CENTRALES

Le mode

Cas des caractères qualitatifs discrets
Cas des caractères quantitatifs discrets
Cas des caracteres quantitatifs continus
Mode principal et mode secondaire

La médiane

Calcul à partir d'un tableau élémentaire
Calcul à partir d'un tableau de dénombrement
Propriété de la médiane
Exemple d'utilisation en géographie

1.3 La moyenne

Calcul à partir d'un tableau élémentaire
Moyenne simple et moyenne pondéré
Calcul à partir d'un tableau de dénombrement
Propriétés de la moyenne
Exemple d'utilisation en géographie

2. VALEURS CENTRALES ET RESUME D'UNE DISTRIBUTION

2.1 Les six propriétés de Yule

(1) Objectivité
(2) Sensibilité
(3) Signification concrète
(4) Simplicité du calcul
(5) Robustesse
(6) Calcul algébrique

2.2 Valeurs centrales et forme des distributions

Distribution multimodale
Distribution unimodale dissymétrique à gauche
Distribution unimodale dissymétrique à gauche
Distribution unimodale symétrique

Pour obtenir un cours de statistique détaillé, mais non centré sur la géographie, cliquez ici.

VOCABULAIRE DU CHAPITRE STAT.3

Valeurs centrales : Le but des valeurs centrales est de résumer en une seule valeur l'ensemble des valeurs d'une distribution statistique. Il existe trois valeurs centrales : le mode, la médiane, la moyenne.

Le mode

Le mode, ou valeur dominante, est la valeur la plus fréquente d'une distribution. Cette valeur se calcule toujours à partir d'un dénombrement des modalités du caractère. Il faut cependant distinguer soigneusement le cas des caractères discrets et celui des caractères continus (Cf. Vocabulaire 2).

Caractère quantitatif ou qualitatif discret

Pour un caractère qualitatif, ou pour un caractère quantitatif discret ayant un nombre de modalités inférieur au nombre d'éléments, le mode est la modalité qui a la fréquence simple la plus élevée (ou l'effectif le plus élevé, ce qui revient au même).

Caractère quantitatif continu Les modalités étant en nombre infini, il est peu probable que deux éléments aient la même valeur. Dans ce cas, le mode ne peut pas être défini directement, il faut au préalable établir une partition en classes (Cf. Vocabulaire Stat.2)

On détermine tout d'abord la classe modale qui est celle dont la fréquence moyenne est la plus élevée C'est la classe où les valeurs sont le plus concentrées mais pas nécessairement celle qui comporte le plus d'individus. Visuellement, la classe modale correspond au sommet de l'histogramme.

Le mode est alors obtenu en prenant le centre de la classe modale, c'est-à-dire la moyenne de ses bornes supérieure et inférieure.

Lorsque l'histogramme d'une distribution présente deux pics séparés par un creux, on dit que la distribution est bimodale. On distingue alors un mode principal et un mode secondaire. Plus rarement, on peut trouver des distributions ayant trois modes et plus.

Exercice: Soit une entreprise de 20 salariés. A l’aide du tableau ci-dessous, déterminez quel est le mode de la distribution des salaires (salaire modal).

tranche de	Effectif	Fréquence
salaire ($)		Simple
[0 ; 1000[	5	25%
[1000 ; 2000[	6	30%
[2000 ; 4000 [	8	40%
[4000 ; 8000]	1	5%
Total	20	100%

La médiane

Réservée aux caractères quantitatifs. Les valeurs du caractère X étant classées par ordre croissant, la médiane est la valeur du caractère qui partage l'ensemble décrit par X en deux sous ensembles d'effectifs égaux : 50 % des éléments ont des valeurs de X supérieures à X _médet 50% prennent des valeurs inférieures.

Calcul à partir du tableau élémentaire : On ordonne le tableau, et on cherche l'élément qui partage la distribution en deux parties égales: on repère l'élément qui a le rang (N+1)/2 pour le caractère X. Si la distribution a un nombre impair d'éléments on trouve une valeur unique qui est la médiane, si la distribution a un nombre pair d'éléments, on trouve deux valeurs qui déterminent un intervalle médian : on prend alors pour médiane le centre de cet intervalle médian.

Calcul à partir de la courbe des fréquences cumulées : (Cf. Vocabulaire 2)

Calcul à partir d'un tableau de dénombrement : On repère la classe j qui contient la médiane, puis on réalise une interpolation linéaire pour estimer la valeur de celle-ci selon la formule :

Médiane = Binfj + [ Aj/ Fj* (0.5-Fascj-1)]

Propriété de la médiane La médiane est la valeur du caractère qui est la plus proche de toutes les autres. C'est celle qui minimise les distances en valeur absolue :

N
S½ xi - A½est minimum si et seulement si A est la médiane de X
i=1

Applications en géographie Le fait que la médiane minimise les distances à tous les points d'une distribution peut être utilisé en géographie pour déterminer des localisations optimales, c'est-à-dire des emplacements dotés de la meilleure accessibilité possible (minimisation de la distance d'un point à tous les autres). Le point médian peut être calculé dans un espace à une dimension (ex. localisation d'un dépôt d'essence desservant l'ensemble des stations services d'une autoroute) ou dans un espace à deux dimensions (localisation d'une école desservant tous les habitants d'une commune). Le calcul du point médian est cependant plus compliqué dans un espace à deux dimension.

Exercice : On veut localiser un dépôt d'essence devant desservir 7 stations services situées sur une autoroutes aux kilomètres 0, 50, 100, 200, 300, 400, 700. Vérifiez que la localisation optimale du dépôt, c'est-à-dire celle qui minimise les distances à toutes les stations se situe au point médian (km 200) et non pas au point moyen (km 250) ou au point central (km 350).

La moyenne

En principe réservée aux caractères quantitatifs continus mais applicable aux caractères quantitatifs discrets.

Calcul à partir du tableau élémentaire :

Moyenne simple

La moyenne simple est égale à la somme des valeurs divisée par le nombre d'éléments.

_ N
x = S x_i / N
i=1

Moyenne pondérée Plus généralement, on recourt à la pondération lorsque les unités n'ont pas le même poids. Si chaque unité i est décrite par sa modalité xi et son poids pi, la moyenne pondérée est :

_ N N
x = S P_i . Xi / S Pi
i=1 i=1

N.B. Dans le cas d'un caractère X correspondant au rapport de 2 stocks V et P (X=V/P) il faut impérativement pondérer le calcul de la moyenne par le dénominateur P si l'on veut trouver la moyenne générale de l'ensemble de référence.

Calcul à partir du tableau de dénombrement On effectue une moyenne pondérée en assimilant chaque classe j à son centre Xc_j et en pondérant par l'effectif n_jde la classe.

_ k k
x = S Xc_j. n_j / N = S Xc_j. f_j
j=1 j=1

Propriétés de la moyenne

1) La somme des écarts à la moyenne est égale à zéro.

N _
S ( x_i - x ) = 0
i=1

2) La moyenne minimise la somme du carré des distances à tous les éléments

N
S( xi - A)² est minimum si et seulement si A est la moyenne du caractère X
i=1

Exercice : Quel serait le PIB par habitant d'une Chine réunifiée avec Tai-Wan ?

Pays	PIB ($ / hab.)	Pop (millions hab.)
Chine Populaire	3500	1300
Taï-Wan	18500	20
Chine réunifiée	?	?

Avantages et inconvénients des différentes valeurs centrales

Le statisticien Yule (XIXème siècle) a définis six propriétés souhaitables pour les valeurs centrales.

(1) Etre définie de façon objective

Deux personnes différentes traitant la même information doivent trouver le même résultat en ce qui concerne le calcul des valeurs centrales. Ceci est vrai pour la moyenne et la médiane mais pas pour le mode qui dépend du choix de la partition en classe adoptée.

(2) dépendre de toutes les observations

La modification d'une seule observation doit entraîner une modification de la valeur centrale. Ceci est vrai de la moyenne mais pas du mode et de la médiane

(3) avoir une signification concrète

Bien que la moyenne paraisse "naturelle" elle est en fait très abstraite alors que le mode peut être défini comme la situation la "plus fréquente" et la médiane comme celle "qui divise en deux la distribution" (un individu sur deux a une valeur inférieure ou supérieure à celle-ci). Le caractère abstrait de la moyenne ressort bien quand on l'applique à des caractères discrets (e.g. que signifie 2.5 enfants par femmes ?)

(4) être simple à calculer

Cette préoccupation du XIXe siècle n'est plus de mise à l'époque des ordinateurs ... Toutes les valeurs centrales sont actuellement simples à calculer.

(5) être peu sensible aux fluctuations d'échantillonage

Il s'agit en apparence de l'inverse de la propriété (2). Mais on peut dire que cette propriété définit la robustesse de la mesure face à des erreurs qui peuvent apparaître (données mal codées, valeurs aberrantes). La moyenne "explose" en présence d'une valeur aberrante alors que la médiane est très robuste. Le mode est en situation intermédiaire

(6) se prêter au calcul algébrique

Lorsque l'on connaît les valeurs centrales de k échantillons E1...Ek d'effectifs respectifs P1...Pk, peut-on retrouver la valeur centrale de E qui est la réunion de tous ces échantillons ? La réponse est affirmative dans le cas de la moyenne mais négative dans ceux du mode et de la médiane. Ceci est un gros avantage de la moyenne en terme de stockage de l'information.

On peut résumer les avantages des différentes valeurs centrales dans un tableau

Propriété de Yule	Mode	Mediane	Moyenne
1) est définie de façon objective	-	+	+
2) dépend de toutes les observations	-	-	+
3) a une signification concrète	+	+	-
4) est simple à calculer	+	+	+
5) est peu sensible aux fluctuations d'échantillonage	-	+	-
6) se prête au calcul algébrique	-	-	+

Valeurs centrales et forme des distributions

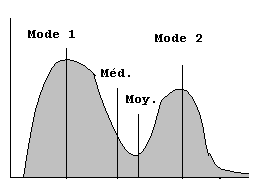
Distribution multimodale

Dans le cas d'une distribution multimodale, il existe plusieurs zones de concentration des valeurs séparées par des discontinuités. Dans ce cas, ni la moyenne, ni la médiane ne peuvent être considérées comme représentatives de la distribution . Le seul résumé statistiquement correct consiste à présenter les différents modes qui permettent de localiser les zones de concentration des valeurs.

Distributions unimodales dissymétriques (à droite ou à gauche)

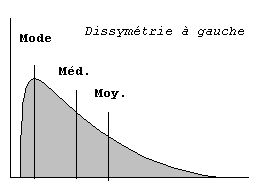
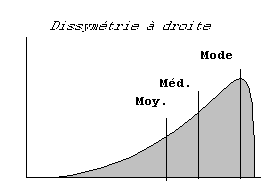
Lorsqu'il existe une zone de concentration principale des valeurs, la distribution est unimodale. Mais la densité des individus peut décroître plus rapidement d'un côté que de l'autre et l'on parle alors de distribution unimodale dissymétrique à gauche ou à droite. Les trois valeurs centrales sont alors nettement séparées et le meilleur résumé statistique est fourni par la médiane.

Distributions unimodales symétriques

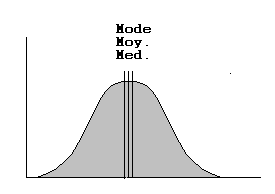
Les trois valeurs centrales sont à peu près confondues et fournissent le même résumé statistique. On préférera en général résumer ces distributions à l'aide de la moyenne qui possède des propriétés algébriques intéressantes (Cf. 6^e pro.de Yule)

EXEMPLES DU CHAPITRE STAT.3