Logithèque pour l'analyse spatiale
Claude Grasland
Université Paris VII / UFR GHSS
Année 2001
LA LOI DE REILLY-HUFF
Exercice n°1 : Influence
du frein de la distance
|
OBJECTIFS DE L'EXERCICE n°1
Le but de cet exercice est de se familiariser avec la loi de Reilly-Huff
à travers un petit exemple théorique où l'on examine
l'évolution de la hiérarchie urbaine et des aires d'influence
urbaines en fonction des variations de l'exposant de la distance. Il s'agit
également de comprendre les différences entre les deux manières
de définir les aires d'attraction urbaine à l'aide du modèle
de Reilly (attraction maximale) et à l'aide du modèle de
Huff (attraction relative).
A) PREPARATION DES DONNEES
Télécharger le logiciel REILLY.EXE dans la logithèque.
Télécharger le fichier de données relatives à
l'exercice n°1 : exo1.txt
Placer le programme et le fichier de données dans le même
répertoire de votre disque dur puis lancez l'application Reilly
en double-cliquant dessus.
Réalisez une première carte indiquant juste la localisation
des villes. Corrigez les valeurs Xmin, Ymin, Xmax, Ymax pour obtenir
un espace d'étude de coordonnées (0,0,100,100).
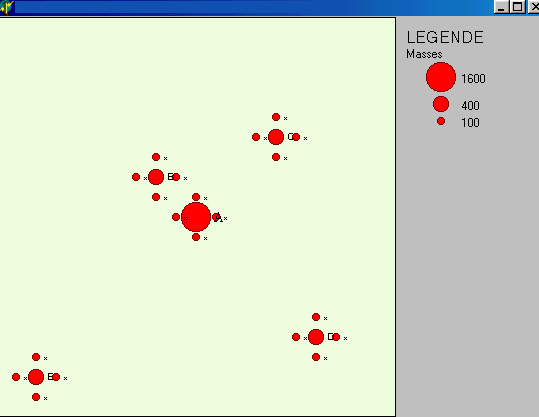
Vous devez obtenir la carte suivante :
| Figure 1 : ESPACE D'ETUDE |
 |
Questions :
-
Quelle est la forme du réseau urbain présenté dans
l'exercice 1 ?
-
Les villes moyennes (B,C,D,E) sont-elles dans des situations équivalentes
?
-
Que peut-on prévoir en ce qui concerne leurs aires d'influence
respectives ?
B) LE MODELE DE REILLY "CLASSIQUE" (exposant de la
distance égal à 2, attraction maximale)
Calculez les liens de dépendance et les aires
d'influence théorique des villes dans l'hypothèse où
la loi de Reilly serait vérifiée (frein de la distance égal
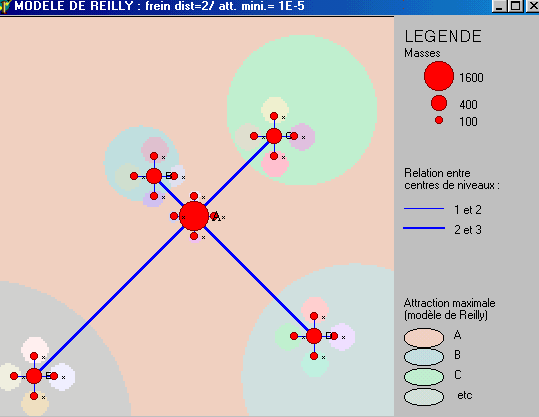
à 2). Vous devez obtenir l'image suivante :
| Figure 2 : MODELE DE REILLY (frein de la distance =2) |
 |
Questions :
-
Quelle est la forme du réseau urbain ?
-
Les villes moyennes (B,C,D,E) sont-elles dans des situations équivalentes
?
-
les petites villes (x) sont-elles dans des situations équivalentes
?
-
Les aires d'influence des villes moyennes sont-elles centrées
sur celles-ci ?
C) LE MODELE DE HUFF (exposant de la distance égal
à 2, attraction relative)
Sans modifier l'exposant de la distance, tracez les
aires d'attraction relative des centres (modèle de Huff) à
la place des aires d'attraction maximale (modèle de Reilly). Vous
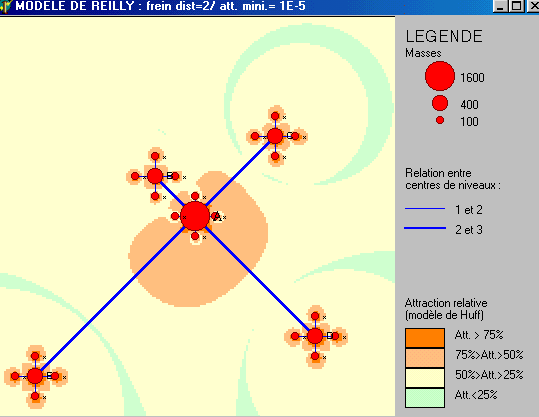
devez obtenir l'image suivante :
| Figure 3 : MODELE DE HUFF (frein de la distance =2) |
 |
Questions :
-
Quelle signification pouvez-vous donner aux différents niveaux
d'attraction relative ?
-
Les différences entre les aires d'attraction des villes moyennes
sont-elles aussi flagrantes que précédemment ?
-
En quoi les aires d'attraction prédites par le modèle
de Huff sont-elles plus réalistes que celles déterminées
précédemment à l'aide du modèle de Reilly ?
-
Quelle hypothèse supplémentaire pourrait être introduite
?
-
D) UTILISATION D'UN FREIN DE LA DISTANCE PLUS FORT
(exposant de la distance égal à 3 ou 4)
Calculez les aires d'attraction prévues par
les modèles de Reilly & Huff en utilisant des freins de la distance
supérieurs à ceux prévus par la version classique
(exposants de la distance égal à 3 ou 4).
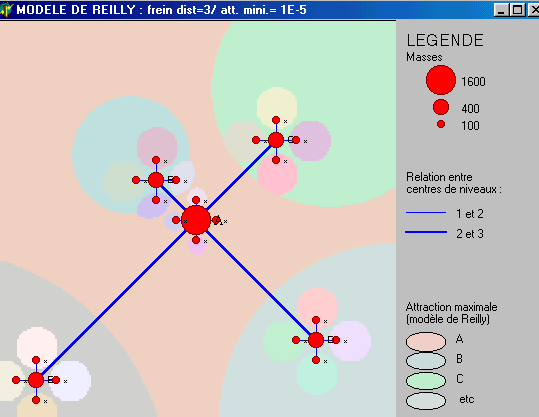
Figure 4 : Modèles de Reilly & Huff
avec des exposants de la distance supérieurs à 2
Exposant
de la
distance
|
Modèle de Reilly
|
Modèle de Huff
|
|
2
|

|

|
|
3
|
|
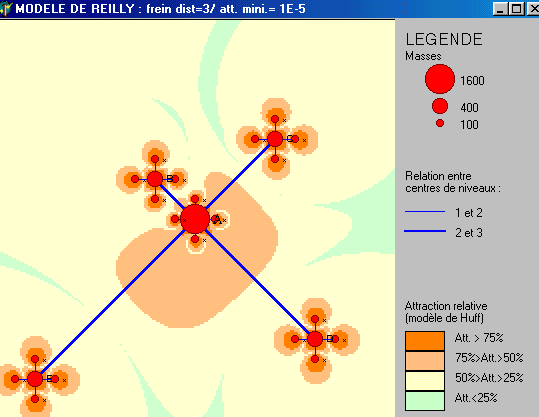
|
|
4
|
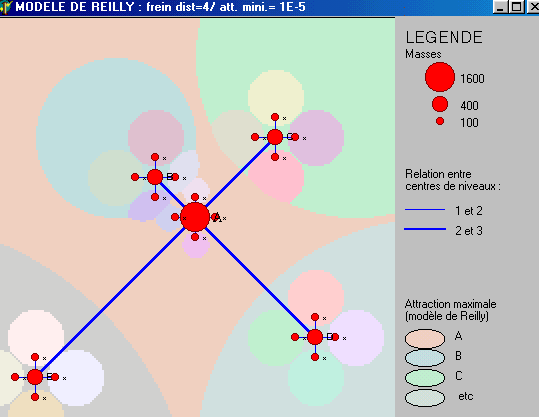
|
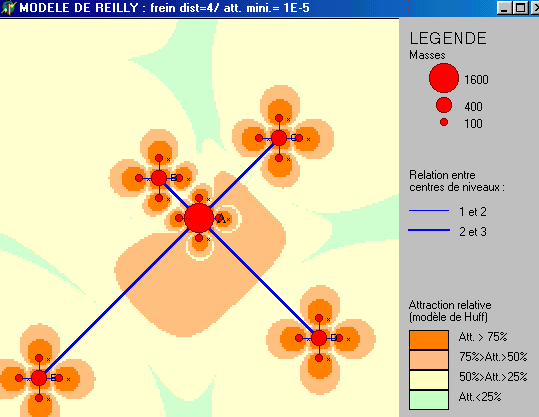 |
Questions :
-
Quelle modifications apparaissent dans les aires d'attraction lorsque
l'effet de la distance diminue ?
-
Quelles villes bénéficient le plus de cet affaiblissement
de l'effet de la distance ?
-
Quels types de comerces ou de services sont susceptibles de correspondre
à l'hypothèse d'un effet réduit de la distance ?
-
Que se passerait-t-il si on avait utilisé un exposant de la distance
très élevé (infini)?
E) UTILISATION D'UN FREIN DE LA DISTANCE PLUS FAIBLE
(exposant de la distance égal à 1 ou 0.5)
Calculez les aires d'attraction prévues par
les modèles de Reilly & Huff en utilisant des freins de la distance
inférieurs à ceux prévus par la version classique
(exposants de la distance égaux à 1 ou 0.5).
Figure 5 : Modèles de Reilly & Huff
avec des exposants de la distance inférieurs à 2
Exposant
de la
distance
|
Modèle de Reilly
|
Modèle de Huff
|
|
2
|

|

|
|
1
|
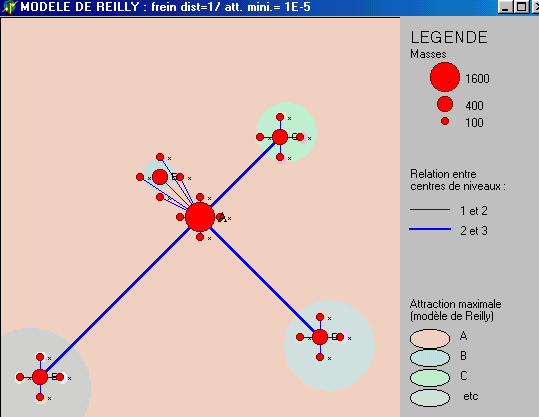
|
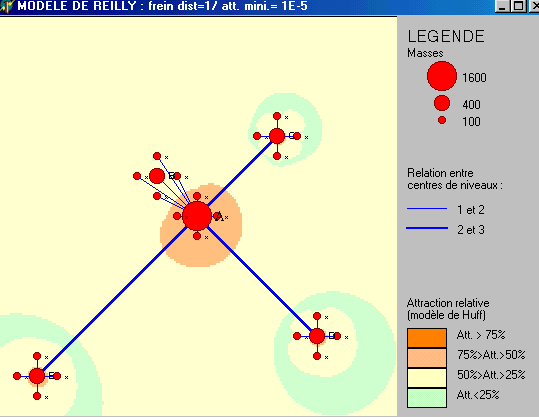
|
|
0.5
|
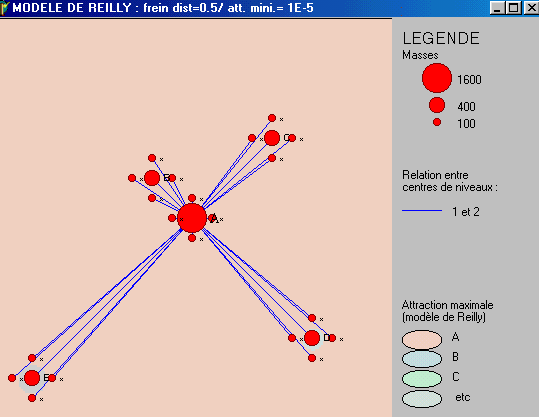
|
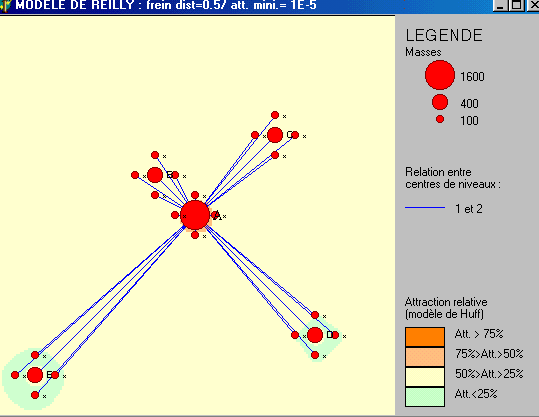 |
Questions :
-
Quelle modifications apparaissent dans les aires d'attraction lorsque
l'effet de la distance augmente ?
-
Quelle modification intervient dans les relations hiérarchiques
des petits centres ?
-
Quelles villes bénéficient le plus de ce renforcement
de l'effet de la distance ?
-
Quels types de comerces ou de services sont susceptibles de correspondre
à l'hypothèse d'un effet important de la distance ?
-
Que se passerait-t-il si on avait utilisé un exposant de la distance
nul ?















