2.2 APPLICATIONS DU CONCEPT D'ACCESSIBILITE EN GEOGRAPHIE ET DANS LES DIFFERENTES SCIENCES SOCIALES
2.2.1 Géographie et transport : comment cartographier les variations de l'accessibilité routière et de son efficacité ?
A la différence des autres sciences sociales, la géographie tend à privilégier des lieux et non pas des acteurs doués d'une capacité de décision dans la définition des mesures d'accessibilité qu'elle produit. Ces lieux peuvent ensuite recevoir un poids économique ou social qui permettra indirectement de tenir compte des acteurs qui nouent effectivement des relations dans l'espace, mais leur appréhension est toujours indirecte et ce que l'on osuhaite avant tout à mesurer ce sont des valeurs moyennes en faisant l'hypothèse implicite que les acteurs localisés en un même lieu subissent les mêmes contraintes de localisation, indépendamment des moyens dont ils disposent pour s'en affranchir (capital, degré de mobilité, etc.).Les géographes, s'ils ne tiennent pas compte des capacités individuelles de mobilité, accordent en revanche une grande importance aux infrastructures de mise en relation des lieux (moyens de transport), à leur efficacité (mesurée en temps de parcours moyen) et éventuellement à leur coût (marginal ou généralisé). Pour certains auteurs il est aberrant de parler d'accessibilité spatiale pour des mesures utilisant la distance euclidienne comme facteur d'éloignement entre les lieux, et le terme devrait être réservé à l'emploi de métriques faisant référence au temps, à la fréquence ou au coût des moyens de transport, l'idéal étant une approche multimodale en terme de coût généralisé.
Les géographes sont enfin très sensible à la transmission cartographique des résultats des mesures d'accessibilité et ils ont développé toute une batterie de solutions originales et innovantes pour visualiser la position relative des lieux (isochrones, anamorphoses, pseudo-relief, etc.).
Notons enfin que les géographes privilégient en matière d'accessibilité les approches quantitatives (résumé de l'accessibilité de chaque lieu à l'aide d'un indicateur unique) au détriment d'approches plus qualitatives s'intéressant à la forme des courbes locales d'accessibilité et non pas à un résumé numérique de celles-ci.
L'établissement d'une représentation continue de l'accessibilité sous la forme d'isolignes suppose que l'on puisse affecter à tout point de l'espace (E) une mesure d'accessibilité à un ensemble de resources (R) pour une certaine mesure d'éloignement spatial.
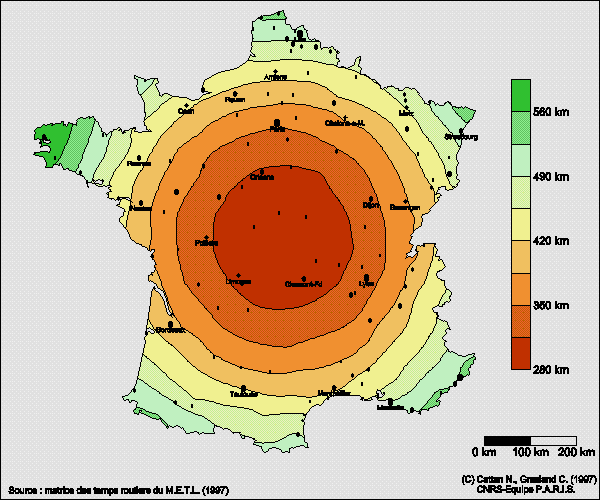
1) Distance euclidienne moyenne d'un point du territoire à l'ensemble de celui-ciLa carte la plus simple d'accessibilité spatiale que l'on puisse produire est la distance euclidienne moyenne d'un point de l'espace considéré (E) à tous les points qui composent celui-ci. Il s'agit donc d'une mesure d'accessibilité interne (P=R=E) qui n'implique aucune hypothèse particulière sur le couple population-ressource et qui dépend uniquement du choix de la métrique considérée pour mesurer les distances. Dans le cas de la distance euclidienne, la seule information nécessaire est la description des points définissant le contour de l'enveloppe territoriale de l'espace étudié.
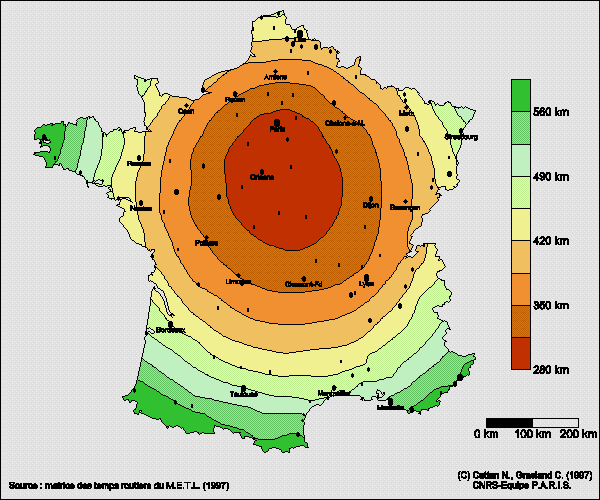
2) Distance euclidienne moyenne d'un point du territoire à l'ensemble de la population française
Tout en conservant la distance euclidienne comme mesure d'éloignement, on peut chercher à mesurer la distance euclidienne moyenne d'un point de l'espace considéré (E) à tous les habitants qui sont localisés à l'intérieur de celui-ci. Il s'agit donc d'une mesure d'accessibilité externe où les positions correspondent à l'ensemble des localisations possibles (surface) et les sites à l'ensemble des localisations occupées par les habitants (resources). L'objectif est donc cette fois-ci de déterminer en quel point du territoire français on se trouve le plus "proche" de l'ensemble de la population française en moyenne.
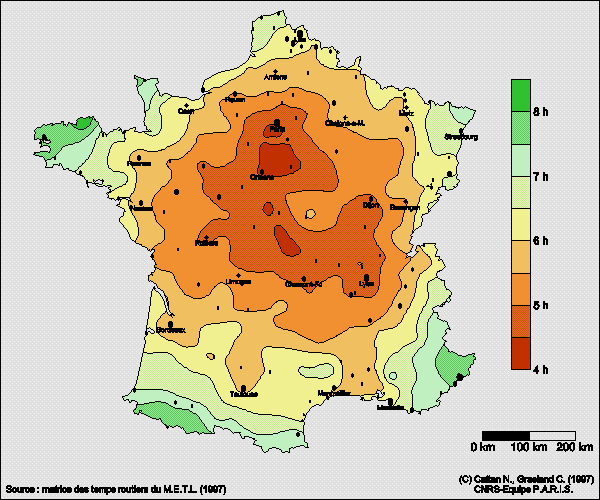
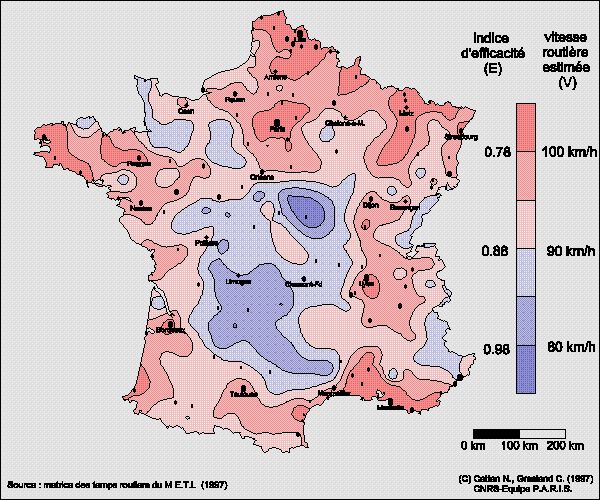
3) Distance routière moyenne d'un point du territoire à l'ensemble de celui-ci
Compte-tenu de la densité du réseau routier, il est possible d'assigner une distance routière à tout couple de points du territoire français au prix d'une approximation peu gênante (calcul des distances dans le cadre de mailles dont le poids est définie par leur surface, puis interpolation des valeurs d'accessibilité entre les centres de mailles). On peut alors proposer une image de l'accessibilité routière définie comme le temps moyen de relation par la route d'un point du territoire français à n'importe quel autre point tiré au hasard.
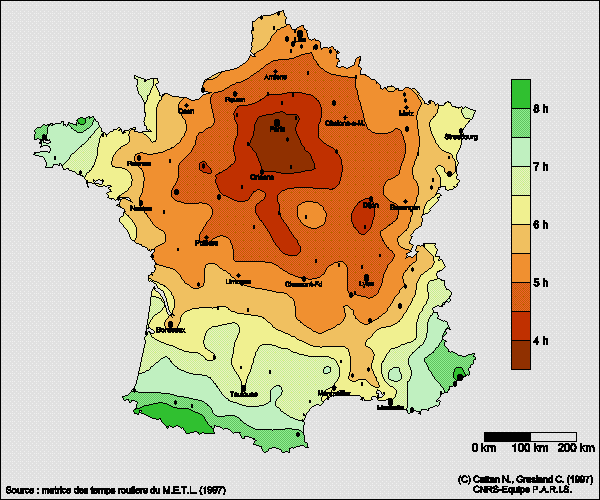
4) Distance routière moyenne d'un point du territoire à l'ensemble de la population française
On peut enfin appliquer la distance routière à la mesure de l'accessibilité de tout point du territoire à l'ensemble de la population française et déterminer ainsi les points du territoire d'où l'on peut rejoindre le plus rapidement par la route l'ensemble de la population française.
5) Utilisation de la distance euclidienne comme modèle de réseau de transport homogène et isotrope et évaluation des variations spatiales de l'efficacité du réseau de transport
Bien que la distance en temps sur un réseau de transport soit a priori plus intéressante que la distance euclidienne en kilomètre pour décrire les localisations à l'intérieur du territoire français, cette dernière peut servir de norme pour mesurer l'efficacité du mode de transport et l'inégale dotation des différents points du territoire en infrastructure. La distance euclidienne est en effet un modèle parfait d'un réseau de transport homogène et isotrope de sorte que les écarts entre l'accessibilité euclidienne et l'accessibilité à l'aide d'un mode de transport peuvent s'analyser comme l'effet d'un excédent ou d'un déficit d'infrastructures permettant la liaison d'un point du territoire avec l'ensemble des autres points de celui-ci ou avec l'ensemble de la population. La seule réserve que l'on puisse émettre à l'encontre de cet indicateur est le fait que les décalages entre distance euclidienne et temps de transport à l'aide d'un mode de transport sont parfois la conséquence non pas de l'absence mais de l'impossibilité d'établir une infrastructure directe, par exemple dans le cas où le trajet euclidien entraîne la traversée d'une étendue maritime. Ce défaut pourrait toutefois être levé si l'on avait substitué à la distance euclidienne l'itinéraire terrestre le plus court en kilomètres.
On pourrait poursuivre l'analyse en étudiant d'autres modes de transport (fer, avion) ou en calculant des mesures d'accessibilité multimodales. Mais il faut alors introduire des hypothèses plus complexes sur la concurrence ou la complémentarité des différents modes de transport et sur les temps ou les coûts d'interconnexion lorsque l'on passe d'un mode à un autre (Cattan N., Grasland C., 1998).
2.2.2 Géographie et économie : le problème des localisations optimales dans l'espace ?
En se limitant à l'analyse d'un texte de J.F. Thisse (1994) illustré de quelques exemples, nous allons montrer l'intérêt d'une réflexion conceptuelle préalable à toute recherche d'une ou plusieurs localisations optimales.
1) Egalité, efficacité ou équité ?
Dans cet exemple très simple, on considère une commune où la répartition est répartie dans trois villages (1, 2, 3) comportant le même nombre d'enfants en âge d'aller à l'école. Chaque village étant très jaloux des autres il faut choisir une localisation pour l'école qui soit justifiée à la fois par des conditions de justice (ne défavoriser les enfants d'aucune commune) et d'efficacité (réduire au maximum le trajet de l'ensemble des enfants).
Dans l'exemple présenté ci-dessus, la localisation la plus égalitaire consiste à localiser l'école au point A qui est équidistant de tous les villages. Tous les enfants parcoureront exactement la même distance pour se rendre à l'école. La solution parfaitement égalitaire n'est cependant possible que lorsqu'il existe trois sites. Dans le cas de deux sites, il existe une infinité de solution satisfaisant le critère (droite d'équidistance) et dans le cas de 4 sites ou plus, il n'existe de solution égalitaire que si les points appartiennent à un même cercle. Si ces conditions ne sont pas vérifiées, on peut définir la solution la plus égalitaire comme étant celle qui minimise les écarts entre les distances parcourues, c'est à dire comme une minimisation de la variance (ou tout autre critère de dispersion) des distances.
Mais on peut objecter que cette solution juste est également peu efficace puisqu'elle impose de long trajets à l'ensemble des enfants. La localisation la plus efficace, c'est-à-dire celle qui minimise la moyenne des distances des enfants consisterait au contraire à localiser l'école au point B. Mais elle entraînerait un accroissement non négligeable des distances parcourues par les enfants du village 1. On pourrait éventuellemment substituer à la moyenne tout autre valeur centrale résumant l'ensemble des distances parcourues par les enfants (mode, médiane, quantiles).
Enfin, la localisation la plus équitable au sens de J. Rawls, c'est-à-dire celle qui minimise la distance maximale parcourue par un enfant (critère maximin). Elle correspond à l'installation de l'école au point C qui correspond à l'intersection de cercles de diamètre minimal centrés sur les points 1, 2 et 3.
Il est bien évident que d'autres solutions optimales pourraient être déterminées, par exemple en construisant une fonction d'utilité qui soit une combinaison pondérée de tout ou partie des critères précédents et en cherchant à la maximiser. Et l'on peut également dans ce cas inverser le modèle et déterminer pour une localisation connue quel est le poids qui a été accordé à chacun des critères (égalité, équité, efficacité) dans le choix d'un site donné.
En tout état de cause, le rôle de l'analyste spatial n'est
pas de trancher le débat essentiellement politique et économique
qui doit guider la sélection des critères, mais simplement
de montrer quelle est la traduction spatiale de tel ou tel choix de critères
et de pondérations sur l'emplacement du site, c'est-à-dire,
de faire prendre conscience aux décideurs politiques de la signification
et des conséquences de leur action (Weber M., Le savant et le politique).
2) Problèmes d'optimisation sous contrainte
On pourrait également ajouter que les trois solutions précédentes
(qui aboutissent à localiser l'école en rase campagne) sont
peu rationelles et qu'il vaudrait somme toute mieux localiser l'école
dans l'un des trois villages. Il s'agit alors d'un problème d'optimisation
sous contrainte (la solution est l'un des trois villages) et l'on peut
trancher en calculant pour chaque village les valeurs correspondant aux
trois critères précédents puis en opérant une
pondération des critères.
| Critère |
|
|
|
| Egalité ecart-type(d) |
|
|
|
| Efficacité moy(d) |
|
|
|
| Justice
max(d) |
|
|
|
Dans le cas présent, aucune pondération n'est nécéssaire puisqu'il apparaît que, quel que soit le critère retenu (égalité, efficacité, équité), c'est le village 2 qui correspond à la solution optimale. Sauf à faire preuve de mauvaise foi ou à introduire de nouveaux critères dans l'analyse, aucune justification ne peut être proposée pour une localisation dans les autres villages.
La situation est cependant souvent plus complexe dans les problèmes de ce type et il peut arriver que chacun des sites possèdent des avantages spécifiques sur l'un ou l'autre des critères d'accessibilité. Le débat doit alors porter sur l'importance à accorder à chacun des critères. Un exemple simple mais démonstratif est fourni par l'article suivant :
C. Helle et S. Passegué (1997), "Quelle localisation optimale pour une nouvelle médiathèque ? L'exemple du réseau de lecture publique dans la Drôme", Espace Géograhique, 26, 4, pp. 367-374
Bien que s'appuyant sur une technologie sophistiquée (emploi d'un SIG-raster pour calculer les accessibilités routières) cet article montre (sans le vouloir) qu'en fin de compte le critère le plus déterminant dans le choix du site optimal est la délimitation qui est faite de la zone de desserte potentielle en début d'analyse et qui avantage très nettement l'une des trois villes candidates. Une approche plus globale, mais qui n'est abordée qu'en fin d'article consisterait à prendre en compte l'ensemble de l'offre et de la demande de lecture sur le département et à examiner, à enveloppe budgétaire fixe, la solution qui augmente le plus l'accessibilité globale de tous les habitants du département à un centre de lecture.
3) Problèmes de localisations optimales multiples
Les problèmes de localisation optimale fondés sur la recherche d'un site unique correspondent en fait à un cas très particulier d'une catégorie beaucoup plus générale de problèmes de localisation optimale visant à localiser plusieurs sites, soit dans un espace vierge, soit dans un espace déjà occupé par des sites que l'on se propose de réorganiser pour optimiser l'accessibilité de la population aux ressources.
Les approches qui sont le plus utilisés sont dérivées de l'économétrie et se fondent sur la recherche de la configuration optimisant une fonction d'utilité globale sous différentes contraintes.
L'un des modèles les plus connus est celui de la p-médiane qui vise à déterminer la localisation optimale d'un nombre fixé de site ayant vocation à desservir une population dont la localisation est connue. La résolution des problèmes de p-médiane est généralement délicate et doit faire appel à des algorithmes puissant car la détermination de l'optimum global ne peut être obtenue par une simple succession d'itérations définissant successivement le site 1, le site 2 ... etc.
Exercice :