4.1 FORME GENERALE D'UN MODELE D'INTERACTION SPATIALE

.
En accord avec Fotheringham et O’Kelly (1989) on peut donner une définition très générale d’un modèle d’interaction comme la mise en relation de quatre ensembles de variables (Tableau 1).
 
 

Tableau 1 : Forme générale d’un modèle d’interaction spatiale
 

F = f(E, A, I)  avec F : une ou plusieurs matrices de dimension [m.n] décrivant les échanges entre m lieux d’origine et n lieux de destinations E : un ou plusieurs vecteurs de dimension [m] décrivant les capacités d’émission des lieux d’origines. A : un ou plusieurs vecteurs de dimension [n] décrivant les capacités d’attraction des lieux de destination. I : une ou plusieurs matrices de dimension [m.n] décrivant le degré de séparation des lieux d’origines et de destination.

L’essence des modèles d’interaction est donc de relier les valeurs de la matrice de relation F avec les valeurs correspondantes des matrices E, A et I sous différentes hypothèses. Différentes familles de modèles peuvent donc être définies en fonction du nombre et de la nature des variables (matrices ou vecteurs) contenues dans les ensembles F, E, A et I.
 

Les différentes étapes de la construction d'un modèle d'interaction spatiale sont les suivantes :

1. Choix de la matrice d'interaction (F)
2. Choix des facteurs d'émission (E) et de réception (F)
3. Choix des facteurs d'éloignement (D)
4. Choix de la fonction de décroissance des interactions en fonction de la distance f(D)
5. Choix de la forme générale du modèle et des contraintes
6. Choix du critère d'ajustement et détermination des paramètres à estimer
 

4.1.1 Choix de la matrice d'interaction (F)

La nature de la matrice F décrivant les flux entre les lieux conditionne en premier lieu la nature des modèles qui pourront être élaboré.

matrice carrée ou matrice rectangulaire

 
Le cas le plus fréquent est celui de l’analyse d’une matrice carrée où il y a identité entre les lieux d’origines et les lieux de destination. C’est par exemple le cas lorsque l’on étudie les échanges de marchandise entre les régions françaises ou le nombre d’avions et de trains entre les villes européennes de plus de 200 000 habitants.
 
 
 

	A	B	C	D	total			X	Y	Z	total
A							A
B							B
C							C
D							D
total							total
	matrice carrée						matrice rectangulaire

Mais il peut également arriver que les flux étudiés concernent des matrices rectangulaire où lieux d’origine et de destination sont différents. C’est par exemple le cas lorsque l’on étudie les flux de marchandise des régions françaises vers les régions belges (sans étudier les relations intra-France ou intra-Belgique) ou bien lorsque l’on étudie les déplacements des étudiants depuis leur lieu de résidence (36000 communes) vers leur lieu d’étude (les sites universitaires).
 

N.B. La distinction matrice carrée / matrice rectangulaire a donc trait non pas au nombre de lignes et de colonnes (il peut arriver qu’une matrice " rectangulaire " comporte le même nombre de lieux d’origine et de destination) mais à l’équivalence ou non des deux listes de lieux d’origine et de destination.
 
 

Les deux types de matrices de flux soulèvent des problèmes d’interprétation et d’analyse de natures différentes. En effet, les matrices rectangulaire sont souvent associées à des problèmes d’allocation de ressources ou d’accessibilité tandis que les matrices carrés se rattachent plus directement à des problèmes d’interaction ou d’équilibre des échanges. Seules ces dernières seront considérées dans le cadre de ce travail.
 
 
 
 

diagonale vide ou diagonale pleine (matrices carrées)

 
Dans le cas des matrices carrés, il faut également opérer une distinction essentielle entre les matrices à diagonale pleines, pour lesquelles le flux d’une unité spatiale vers elle-même est définie et les matrices à diagonale vides pour lesquelles ce flux n’est pas défini.
 
 
 

	A	B	C	D	total			A	B	C	D	total
A	100	10	30	10	150		A	-	10	30	10	50
B	10	200	40	20	270		B	10	-	40	20	70
C	20	50	100	30	200		C	20	50	-	30	100
D	10	30	20	50	110		D	10	30	20	-	60
total	140	290	190	110	730		total	40	90	90	60	280
	diagonale pleine							diagonale vide


 

Dans le cas d’une matrice d’échanges migratoires, par exemple, le fait de ne pas renseigner la diagonale signifie que l’on ne considère comme migrants que les individus ayant franchi les limites d’une maille territoriale. Ceci revient à dissocier la probabilité générale de migration en deux composantes indépendantes, le choix d’une destination à l’intérieur de sa propre maille territoriale et le choix d’une destination localisée dans une autre maille territoriale. Or, ce postulat d’indépendance entre les probabilités de migration intra-maille et inter-maille n’est généralement pas vérifié, les taux de migrations variant le plus souvent en fonction inverse de la population ou de la superficie des unités spatiales.
 

Pour autant, la prise en compte des migrations intra-maille (étude d’une matrice à diagonale pleine) soulève toute une série de difficultés tant sur le plan théorique que sur le plan statistique. La diagonale peut en effet correspondre soit à l’ensemble de la population demeurée dans la maille au cours de la période de temps étudiée, soit à la population ayant effectuée un déplacement à l’intérieur de la maille. Mais dans ce dernier cas, l’effectif de migrant dépend du choix d’un maillage interne dont la finesse va conditionner le nombre de migrant intra-maille (e.g. étude des migrations intra-régionales à l’aide d’un découpage départemental, cantonal, communal, domiciliaire, etc). D’un point de vue statistique, la prise en compte des flux intra-maille pose également problème dans la mesure où les distances internes sont généralement difficiles à évaluer et où les biais introduits par cette estimation imparfaite vont d’autant plus se répercuter sur l’ensemble du modèle que les effectifs des flux intra-maille sont généralement très supérieurs à ceux des flux inter-mailles. Seuls des modèles complexes, articulant plusieurs niveaux d’analyse permettent donc de traiter valablement le cas des matrices à diagonale pleine.
 
 

Dans le cadre de cette étude, on se limitera donc à l’étude des modèles d’interaction portant sur des matrices carrées à diagonale vide, tout en soulignant qu’il se fondent sur une hypothèse forte d’indépendance entre le choix des destinations intra-maille et inter-mailles.
 
 
 

agrégation ou désagrégation des flux en sous-populations

Qu’elles concernent des marchandises ou des individus, les matrices de flux ont souvent trait à des agrégats (de population, de marchandise) qui peuvent être segmentés en sous-populations (ce terme étant pris au sens statistique et non pas au sens démographique). En amont de toute modélisation de l’interaction spatiale, il faut donc se demander si l’hypothèse d’homogénéité du comportement de l’agrégat est valide et si, au contraire, il n’y aurait pas avantage à segmenter le modèle d’interaction spatiale en autant de sous-modèle qu’il y a de sous-populations.

Tableau 2 : Effet de barrière et frein de la distance subis par les marchandises échangées entre les régions belges et françaises en 1989

	Frein de la distance	Effet de Barrière	Qualité d'ajustement
NST0	-1.59	4.0	90.5%
NST1	-1.51	5.6	93.8%
NST2	-	-	-
NST3	-2.17	4.8	96.1%
NST4	-	-	-
NST5	-0.93	4.3	92.0%
NST6	-1.72	8.3	90.5%
NST7	-1.53	4.5	90.5%
NST8	-1.10	3.7	90.5%
NST9	-1.25	4.2	90.6%
Ensemble	-1.60	5.6	93.9%

Les paramètres ont été estimés à l’aide d’un modèle à double contrainte selon  le critère de minimisation du Chi-2
Source : Robert D., Sebire V., Grasland C., Calzada C., 1996

 
 

Dans le cadre d’une étude sur les échanges de marchandises entre les régions de France et de Belgique en 1989, on a pu définir les valeurs moyennes du frein de la distance (-1.6 pour une fonction parétienne) et de l’effet de barrière subi au franchissement de la frontière (réduction relative des flux internationaux par 5.6, comparativement aux flux intra-nationaux). Mais ces deux paramètres obtenus tous types de marchandises confondus subissent des variations importantes lorsque l’on effectue les mêmes calculs par types de produits (NST), les produits pondéreux à faible valeur ajoutée subissant davantage le frein de la distance et l’effet de barrière que les produits à forte valeur ajoutée.
 

Le choix d’une modélisation agrégée ou désagrégée par sous-populations dépend fondamentalement des hypothèses faites sur la nature des flux étudiés et sur les relations d’indépendance ou au contraire de concurrence et de substitutions possibles entre les déplacements des différentes sous-population. En tous les cas, l’hypothèse de l’existence d’un comportement moyen indépendant de celui des sous-population doit dans tous les cas être discutée et critiquée lorsque l’information disponible le permet.

4.1.2 Choix des facteurs d'émission (E) et de réception (R)

Variables exogènes caractérisant les lieux d’émission et de réception

 
Les modèles d’interaction spatiale ayant une vocation prédictive privilégient comme facteur d’émission ou de réception des variables exogènes au modèle d’interaction spatiale, c’est-à-dire ne supposant pas une connaissance préalable de la matrice des flux. L’exemple le plus classique est celui de l’emploi de la population totale comme variable censée refléter les capacités d’émission et de réception des lieux dans les modèles d’interaction spatiale décrivant les flux migratoires entre des villes, des régions ou des pays.

On remarquera toutefois qu’il existe une dissymétrie entre les justification théoriques de l’emploi de la population comme mesure des capacités d’émission et de réception dans les modèles migratoires. En tant que capacité d’émission (facteur " push "), la population reflète le nombre d’individus soumis au risque de migrer, ce qui ne soulève pas de difficultés particulière, tout au moins dans les pays où la liberté de déplacement est garantie à tous les citoyens. Le choix de cette même population comme capacité de réception (facteur " pull ") est beaucoup moins évident puisque ce qu’il s’agit de déterminer est la capacité d’accueil des migrants qui dépend de nombreux facteurs (emplois disponibles, logements libres, image de marque, etc.). Ce n’est donc qu’au prix d’une hypothèse assez forte de proportionnalité entre les capacités d’accueil et la taille du lieu de destination que l’on peut utiliser la même variable comme facteur d’émission et de réception.

Cette dissymétrie saute davantage aux yeux lorsque l’on étudie un phénomène tel que les navettes domicile-travail. Il est alors évident que la capacité d’émission doit être définie comme la population active au lieu de résidence et la capacité de réception comme le nombre d’emploi disponibles, soit deux quantités de nature tout à fait différente.

Plus généralement, l’hypothèse de stricte proportionnalité entre les variables décrivant les capacités d’émission ou de réception des lieux et la quantité de flux qu’ils engendrent peut être soumise à critique et de nombreux modèles d’interaction spatiale préconisent l’emploi de paramètres d’élasticité (exposants variables) afin de tenir compte d’effets possibles de non linéarité. L’emploi de ces exposants n’est toutefois pleinement justifié que si les lieux émetteurs et récepteurs correspondent à des entités spatiales pertinentes pour lesquelles la taille peut être un facteur déterminant des capacités d’émission et de réception (villes, pays). Il est beaucoup plus discutable sur le plan théorique lorsque les entités spatiales sont un simple cadre arbitraire d’observation du phénomène (régions, unités de recensement).
 
 

Il existe une dissymétrie conceptuelle entre les variables susceptibles de refléter les capacités d’émission et de réception, leur identité constituant a priori un cas exceptionnel. L’hypothèse de proportionnalité entre ces variables et la quantité de flux générée n’est pas obligatoire et des exposants peuvent être introduits pour tenir compte d’effets de taille non linéaires.
 
 
 

Variables endogènes définies par les sommes marginales de la matrice des flux

 

Les modèles d’interaction spatiale à vocation descriptive ou explicative recourent fréquemment aux sommes marginales de la matrice des flux pour définir les capacités d’émission et de réception des lieux. On note habituellement O_i la somme des flux ayant pour origine le lieu i et Dj la somme des flux ayant pour destination le lieu j.
 

O_i = S _j F_ij

D_j = S _i F_ij
 

Les vecteurs O et D correspondent alors à des variables endogènes du modèle puisqu’ils supposent une connaissance au moins partielle de la matrice des flux. De tels modèles ne permettent donc pas directement de prévoir l’évolution globale des échanges, mais autorisent une reconstitution conditionnelles des échanges entre les lieux (affectation des flux entre les couples origine-destination), une fois connus ou estimés les facteurs de génération des échanges. En d’autres termes, les modèles d’interaction spatiale utilisant les sommes marginales des flux comme capacité d’émission et de réception ne constituent qu’un sous-modèle dans une démarche prédictive et ils imposent le recours à d’autres sous-modèles préalables pour estimer l’évolution des capacités marginales d’émission et de réception au cours du temps.

En règle générale, l’introduction des sommes marginales dans un modèle d’interaction spatiale se traduit par l’apparition de contraintes de conservation des flux portant sur les origines, les destinations ou les deux à la fois . Dans ce cas, l’ajout d’autres variables exogènes est le plus souvent superflu, leurs effets étant absorbé par les contraintes de conservation du modèle.
 

Les modèles d’interaction spatiale utilisant les sommes marginales de la matrice des flux comme capacités d’émission et de réception des lieux correspondent à une classe particulière de modèles dont la vocation est davantage descriptive et explicative que prédictive. Ils peuvent toutefois faire partie d’une chaîne de modèle prédictifs, à condition que l’évolution des sommes marginales au cours du temps soient elles-mêmes estimées à l’aide de variables exogènes.
 
 

Variables d’environnement (opportunités intermédiaires et opportunités groupées)
 
 

Le fait de ne prendre en compte que les caractéristiques de site dans la définition des capacités d’émission et de réception des lieux a été critiqué par de nombreux auteurs qui proposent d’introduire dans les modèles d’interaction spatiale des variables d’environnement ayant trait à la situation des lieux. En effet, la quantité de flux émis par un lieu i vers un lieu j dépend non seulement des caractéristiques propres de ces deux lieux, mais également de l’influence d’autres lieux k, l, m … susceptibles d’attirer les flux en provenance du lieu i ou de saturer les opportunités d’accueil du lieu j. Ces phénomènes d’interaction systémique peuvent être pris en charge par la forme du modèle (introduction de contraintes) mais ils peuvent également être introduits sous la forme de variables spécifiques d’environnement.

Le sociologue S. Stouffer (1940) a par exemple montré que la décroissance des flux en fonction de la distance pourrait être interprété comme l’effet de la présence d’opportunités interposées, que l’on peut modéliser à l’aide d’un processus d’examen séquentiel d’examen des destinations possibles classées par distance croissante. Dans ce cas, l’effet de la distance ne correspond pas à un effet mécanique (continu) mais à un modèle de choix discret de nature séquentielle (ordinal). A titre d’exemple, deux individus physiquement éloignés mais séparés par un désert auront selon Stouffer plus de chance d’entrer en relation que deux individus physiquement proches mais séparés par une zone densément peuplé. Il conviendrait donc de substituer aux mesures habituelles de distance une mesure du nombre d’opportunités interposées, censées mieux décrire le comportement migratoire.

La théorie des opportunités groupées de A.S. Fotheringham (Fotheringham & O Kelly, 1989, Stilwell & Congdom, Chap. 4, 1991) part de prémices similaires et aboutit à une conclusion de portée plus générale sur les effets de l’agrégation et de l’autocorrélation spatiale.
 
 

Dans l’exemple présenté ci-dessus, un migrant localisé en i se trouve à la même distance d’opportunités 1..7 de poids équivalent et il a a priori autant de chance de choisir l’une ou l’autre de ces destinations. Mais le fait que les opportunités 4 à 7 soient spatialement proches peut contribuer à les rendre plus attractives (effet d’agglomération) ou moins attractives (effet de compétition). L’introduction de variables d’environnement décrivant la situation relative d’un lieux permet précisément de mesurer ces effets et de déterminer dans quels sens ils influent sur la distribution des flux.
 
 

On considère de plus en plus que la définition des capacités d’émission et de réception des lieux ne doit pas se limiter aux caractéristiques de site mais peut également prendre en compte des effets de situation. De nouvelles formulations des modèles d’interaction spatiale permettent de prendre en compte ces effets systémiques, soit par l’ajout de contrainte, soit par l’introduction de nouvelles variables d’éloignement (Stouffer), d’émission ou de réception (Fotheringham)

 

4.1.3 Choix des facteurs d'éloignement (D)

Le choix d’une (ou de plusieurs) matrices d’éloignement constitue probablement l’étape la plus importante dans la formalisation d’un modèle d’interaction spatiale. C’est en effet l’introduction d’un facteur d’éloignement spatial ou territorial dans l’explication et la modélisation des échanges qui constituent l’apport décisif de ce type de modèles par rapport à des approches de type économique (flux de marchandises) ou sociologiques (déplacement de personnes).qui vont privilégier d’autres déterminants de l’interaction (complémentarité, identité, concurrence, etc.). On observera toutefois que, d’un strict point de vue mathématiques, il n’y a pas de différence véritable entre les mesures de proximité spatiale et les mesures de proximité sociale ou de complémentarité économique. Des modèles d’interaction complexe peuvent donc tout à fait combiner des métriques relevant de champs disciplinaires différents, lorsque la nature du phénomène le justifie.

Même en s’en tenant provisoirement aux mesures de proximité spatiale, il faut insister sur la diversité des solutions possibles pour mesurer l’éloignement de deux lieux et sur les conséquences du choix d’une métrique plutôt que d’une autre en terme de performance des modèles (qualité d’ajustement) et de signification des résultats obtenus.
Comme il est difficile de brosser un portrait exhaustif des solutions possibles (le choix de la métrique dépendant de la nature du phénomène étudié) on se bornera à évoquer sur un exemple précis, celui des migrations en Tchécoslovaquie, la diversité des choix qui peuvent se présenter.
 
 
 
 

Figure 1 : Les 10 régions de tchécoslovaquie en 1989

 
 

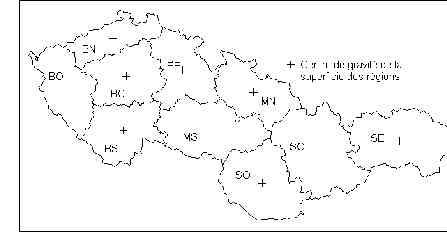
distance entre centres représentatifs des unités spatiales

 
 

On peut tout d’abord observer que le problème de la mesure des distances entre les unités spatiales se posent de façon très différentes selon que l’on a affaire à des unités spatiales de type ponctuelles (assimilable à des points à un certain niveau d’observation) telles que les villes ou selon que l’on a affaire à des unités aréales (issues d’une partition exhaustive de l’espace par un maillage) telles que des régions ou des Etats. Dans le premier cas, l’erreur commise en assimilant l’ensemble des individus contenus dans l’unité spatiale à un point représentatif est négligeable alors que dans le second on doit considérer que la mesure d’éloignement entre les deux régions est une valeur moyenne qui peut avoir une variance assez forte.

Dans le cas des migrations tchécoslovaques, les individus qui partent d’une région vers une autre peuvent théoriquement partir de n’importe quel point de la première et arriver en n’importe quel point de la seconde. Une première solution pour mesurer la distance entre deux régions consiste à assimiler chaque population régionale à une masse unique localisée au centre géométrique des polygones définissant les régions et à calculer la distance euclidienne entre ces centres géométriques (Tableau 3) Cette méthode présente l’avantage de ne nécessiter aucune information autre que le contour des unités territoriales.

Si l’information le permet, on pourrait substituer au centre géométrique de la superficie un point jugé plus représentatif tel que le chef-lieu de la région ou la localisation de la ville la plus importante.

On pourrait également utiliser le centre de gravité de la population plutôt que celui de la superficie, afin de tenir compte de l’inégal répartition de la population à l’intérieur des régions et du caractère éventuellement excentré du chef-lieu. Mais ceci implique que l’on connaisse la distribution de la population à un niveau plus fin que celui des régions (par exemple celui des 114 districts dans le cas tchécoslovaque). Or, si tel est le cas, il vaut mieux abandonner la méthode centroïde et recourir à une mesure plus précise de la distribution des distances entre les habitants.
 

Tableau 3 : Distance entre les centres de gravité de la superficie des 10 régions de Tchécoslovaquie en 1989
 

dij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE
BC	0	97	108	71	101	175	227	307	365	497
BS	97	0	126	165	151	154	241	264	347	490
BO	108	126	0	120	208	264	331	386	460	597
BN	71	165	120	0	136	235	267	369	415	539
BE	101	151	208	136	0	115	131	246	280	404
MS	175	154	264	235	115	0	101	134	196	337
MN	227	241	331	267	131	101	0	163	156	273
SO	307	264	386	369	246	134	163	0	113	254
SC	365	347	460	415	280	196	156	113	0	146
SE	497	490	597	539	404	337	273	254	146	0

distance moyenne entre les populations

 
La distance moyenne entre les habitants de deux régions peut en effet être estimée à l’aide d’une moyenne pondérée des distances entre unités de taille inférieures qui composent les régions. Ainsi, si une région A se compose de n districts 1..i..n et une région B de m districts 1..j..m, la distance moyenne entre les habitants des régions A et B peut être estimée par la formule suivante :
 

d(A,B) = (S _i S _j P_i.P_j.d_ij) / (S _i S _j P_i.P_j)

La précision sera d’autant plus grande que les unités servant de base au calcul sont de petite taille. Dans le Tableau 4 on a utilisé la distribution de la population des 114 districts en 1989 pour estimer la distance moyenne entre les habitants des 10 régions. Des différences significatives apparaissent entre cette distance et la précédente (Tableau 3). Ainsi, la distance moyenne entre les habitants de Bohême-centre et de Bohême-nord est de 86 km alors que la distance entre leurs centres de gravité n’était que de 71 km (-17%). L’écart s’explique par l’allongement de la région de Bohême-nord. Inversement la distance moyenne entre les populations de Moravie-Nord et de Slovaquie-Centre est de 123 km alors que la distance entre les centres géométriques des deux régions est de 156 km (+26%). L’erreur est cette fois-ci imputable à la localisation de la population de Moravie-Nord dont le centre de gravité est situé beaucoup plus au nord-est que le centre géométrique de la région. A partir de la même information (distance entre les districts qui composent les régions), on pourrait également calculer une distance minimum, une distance maximum, une distance médiane, etc.
 

Tableau 4 : Distance moyenne entre les habitants des régions Tchécoslovaques en 1989 (estimée à partir de la distribution par districts)
 

dij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE
BC	0	105	98	86	109	192	273	304	360	518
BS	105	0	118	176	159	167	282	253	341	505
BO	98	118	0	124	200	264	361	362	439	600
BN	86	176	124	0	140	252	309	368	409	559
BE	109	159	200	140	0	135	178	251	277	426
MS	192	167	264	252	135	0	132	128	179	341
MN	273	282	361	309	178	132	0	180	123	253
SO	304	253	362	368	251	128	180	0	141	286
SC	360	341	439	409	277	179	123	141	0	173
SE	518	505	600	559	426	341	253	286	173	0

distance topologique entre les mailles (k-contiguïté)

 
La distance topologique de plus court chemin se fonde sur l’examen du graphe de contiguïté des régions. Deux régions sont situées à une distance topologique de 1 si elles ont une limite administrative commune. Elles sont situées à une distance topologique de 2 si il faut traverser au moins deux limites administratives pour aller de l’une à l’autre, etc. Différentes formules mathématiques permettent de calculer l’ensemble des distances topologiques de plus court chemin à partir du relevé de la simple matrice des contiguïtés d’ordre 1 . Dans le cas de la Tchécoslovaquie l’analyse des contiguïtés permet de calculer la matrice de distance topologique de plus court chemin présentée dans le Tableau 5. La valeur maximale est de 4 (distance entre la Slovaquie orientale et les régions de Bohême-centre, Bohême-ouest ou Bohême-nord).

Tableau 5 : Distance topologique de plus court chemin entre les 10 régions de Tchécoslovaquie
 

dij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE
BC	0	1	1	1	1	2	2	3	3	4
BS	1	0	1	2	1	1	2	2	2	3
BO	1	1	0	1	2	2	3	3	3	4
BN	1	2	1	0	1	2	2	3	3	4
BE	1	1	2	1	0	1	1	2	2	3
MS	2	1	2	2	1	0	1	1	1	2
MN	2	2	3	2	1	1	0	2	1	2
SO	3	2	3	3	2	1	2	0	1	2
SC	3	2	3	3	2	1	1	1	0	1
SE	4	3	4	4	3	2	2	2	1	0

De prime abord, une métrique topologique semble moins intéressante qu’une métrique continue et paraît soumis à toute une série de biais (imprécision, forme des unités territoriales pouvant introduire des raccordements sur quelques kilomètres de frontière) mais l’expérience montre qu’elle donne souvent des résultats équivalents voire supérieurs à ceux des métriques euclidiennes (en terme de qualité d’ajustement des flux migratoires). Ce résultat étonnant semble lié au fait que les maillages territoriaux ne sont généralement pas des constructions arbitraires et qu’ils possèdent des propriétés démographiques (variation de la superficie en fonction de la densité), sociologiques (cohésion sociale) et économiques (cohérence du système productif) qui peuvent en faire de bons marqueurs des proximités territoriales entre les lieux. Il est donc souvent intéressant de confronter leurs résultats à ceux des métriques euclidiennes, voire de combiner les deux à l’intérieur d’un même modèle.
 
 

transformation ordinale d’une métrique continue
 

On peut déduire toute une série d’autres mesures de distances à partir des précédentes. Ainsi, la distance euclidienne entre les centres géométrique des régions (Tableau 3) peut-être transformée en distance ordinale. Pour chaque région, on remplace la distance aux autres régions par un rang, calculé en fonction de l’ordre des distances aux autres régions. Cette matrice présente toutefois le défaut d’être dissymétrique. Ainsi, la région la plus proche de la Bohême-Sud est la Bohême-Centre (d_ij=1) alors que, en sens inverse, la région la plus proche de la Bohême-Centre est la Bohême-Nord et que la Bohême-Sud n’arrive qu’en deuxième position (d_ji=2). Si l’on veut conserver à la distance sa propriété de symétrie, on effectuera la moyenne des rangs dans les deux directions, ce qui donne une distance ordinale symétrique (Tableau 6). On pourrait naturellement calculer la distance ordinale symétrique à partir d’une autre matrice initiale de distance kilométrique.

Tableau 6 : Distance ordinale symétrique entre les régions de Tchécoslovaquie (d'après la distance euclidienne entre les centres géométriques).
 

dij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE
BC	0	1.5	2.5	1	2	5	5.5	7	7.5	8
BS	1.5	0	2.5	4.5	4	4	6	6.5	7	7.5
BO	2.5	2.5	0	2	5	6.5	7.5	8	8.5	9
BN	1	4.5	2	0	3.5	6	6.5	7.5	8	8.5
BE	2	4	5	3.5	0	2	2.5	5.5	6.5	7
MS	5	4	6.5	6	2	0	1	2.5	5	6.5
MN	5.5	6	7.5	6.5	2.5	1	0	3.5	3	5.5
SO	7	6.5	8	7.5	5.5	2.5	3.5	0	1	3.5
SC	7.5	7	8.5	8	6.5	5	3	1	0	1.5
SE	8	7.5	9	8.5	7	6.5	5.5	3.5	1.5	0

L’intérêt théorique de la distance ordinale, symétrique ou non, est de restituer, dans une certaine mesure, les hypothèses de Stouffer sur le rôle des opportunités intermédiaires dans la décroissance des flux avec la distance (Cf. 1.2.3 ). En effet, cette métrique définit l’éloignement de deux régions non pas de façon absolue mais de façon relative, tenant compte de la position des autres régions, plus proches ou plus éloignées. Elle ne restitue toutefois que très partiellement les hypothèses de Stouffer puisqu’elle ne prend pas en compte la population des régions dans le calcul des éloignements relatifs.

4.1.4 Choix de la fonction de décroissance des interactions en fonction de la distance f(D)

fonction exponentielle et fonction puissance (Paréto)

 
Le choix d’une mesure d ’ éloignement (que l’on appellera distance par commodité d’écriture) ne préjuge pas de la forme de son effet sur les interactions. Inspirés d’analogies avec la physique newtownienne (modèle gravitaire) ou l’électricité (potentiel), les premiers modèles d’interaction spatiale utilisaient essentiellement des fonctions puissance négative à exposant entier, la décroissance des flux avec la distance étant censée obéir à une loi de type 1/d_ij ou 1/d_ij². Il est toutefois rapidement apparu aux observateurs des phénomènes d’interaction que les paramètres empiriques optimaux pouvaient prendre des valeurs non entières et qu’il n’y avait pas de raisons théoriques justifiant une stricte analogie entre les phénomènes physiques et les phénomènes sociaux ou économiques. On a donc proposé d’utiliser des fonctions paramétriques de décroissance des interactions avec la distance, les deux plus fréquentes étant la fonction puissance négative (dite aussi de Paréto) et la fonction exponentielle négative.

I_ij = exp(-a d_ij) : fonction d’interaction spatiale exponentielle

I_ij = d_ij^-a : fonction d’interaction spatiale parétienne

Le paramètre a , généralement appelé frein de la distance, n’est pas fixé a priori et est estimée empiriquement de manière à maximiser la qualité de l’ajustement (modèle gravitaire) ou à assurer une contrainte de conservation du coût total de déplacement à l’intérieur du système (modèle de Wilson).

Ces modèles sont au demeurant formellement identiques puisque, si l’on remplace la distance par son logaritme, le modèle de Paréto correspond à un modèle exponentiel . Inversement, le modèle exponentiel correspond à un modèle de Paréto si l’on remplace la distance par son exponentielle.On peut donc passer du modèle exponentiel au modèle puissance par une simple transformation (exponentielle ou logarithmique) de la matrice de distance, c’est-à-dire par l’introduction d’une hypothèse sur le rôle additif ou multiplicatif de la distance sur la décroissance des probabilités de relation entre les migrants. Les études empiriques sur les migrations de population montrent que, d’une manière générale, le modèle exponentiel décrit mieux le comportement des migrants à longue distance, tandis que le modèle puissance décrit mieux le comportement des migrants à longue distance. De ce fait, certains auteurs préconisent d’effectuer la moyenne des deux modèles après estimation séparée (Poulain M., 1981).
 

Au total, s’il semble exister un consensus pour utiliser des fonctions d’interaction spatiale à paramètres variables plutôt qu’à valeurs fixes, le choix d’une forme parétienne ou d’une forme exponentielle demeure un objet de débat. De nombreux auteurs considèrent toutefois qu’il s’agit d’un faux problème et qu’il faut utiliser le modèle fournissant la meilleur description de la situation observée.
 
 

Influence du choix du facteur d’éloignement et de la forme de la fonction d’interaction spatiale sur les résultats.

 
Pour illustrer l’influence du choix de la distance et de la fonction d’interaction spatiale sur les résultats de la modélisation, nous avons appliqué les quatre distances définies précédemment (Tableau 3 à Tableau 6) et les deux fonctions d’interaction spatiale (exponentielle et Paréto) à l’exemple des migrations entre les 10 régions de Tchécoslovaquie en 1961-1965. Dans chaque cas, l’ajustement a été effectué à l’aide d’un modèle d’interaction spatiale multiplicatif à double contrainte et le paramètre de frein de la distance retenu est celui qui correspond à la qualité d’ajustement la meilleure pour le critère de minimisation du chi-deux.
 

Tableau 7 : Variation de la qualité d'ajustement en fonction du choix de la distance et de la fonction d'interaction spatiale (migration entre les régions de Tchécoslovaquie au cours de la période 1961-65)
 

Distance	Fonction	paramètre	Qualité d'ajustement
		de la distance	Chi-deux	r2	r*2
Aucune	-	-	327922	38.0%	0.0%
Euclidienne	Paréto	-1.34	52365	90.1%	84.0%
	Exponentiel	-0.0056	92879	82.4%	71.7%
Moyenne	Paréto	-1.34	90316	82.9%	72.5%
	Exponentiel	-0.0054	116680	77.9%	64.4%
Topologique	Paréto	-1.40	90948	82.8%	72.3%
	Exponentiel	-0.743	109711	79.3%	66.5%
Ordinale	Paréto	-0.89	36859	93.0%	88.8%
	Exponentiel	-0.267	48419	90.8%	85.2%

Le calcul du modèle aléatoire (double contrainte sans effet de la distance) montre que les différences de capacité d’émission et de réception des régions expliquent à elle seules 38% des écarts au modèle de répartition homogène des flux. Quelles que soient la distance ou la fonction d’interaction spatiale retenue, l’introduction d’une fonction d’interaction spatiale permet d’améliorer considérablement la qualité d’ajustement (r2 > 75 %). Dans tous les cas, l’utilisation de la fonction puissance donne des résultats meilleurs que la fonction exponentielle, ce qui est conforme aux résultats empiriques obtenus par d’autres auteurs sur les migrations à moyenne et longue distance.

On aurait cependant tord de considérer que la qualité d’ajustement suffit à trancher entre plusieurs hypothèses de modélisation (choix des distances et de la forme de la fonction d’interaction). Dans l’exemple tchécoslovaque, il existe en effet un facteur latent (effet de barrière migratoire entre les régions des deux républiques tchèques et slovaques) qui est mieux pris en charge par certaines métriques que part d’autres, mais moins en raison de leur qualité intrinsèque qu’en raison précisément de leurs défauts et des déformations qu’elles imposent par rapport aux distances réelles entre les habitants. Le fait que la distance euclidienne entre centre géométrique décrivent mieux les flux que la distance moyenne entre habitant n’a pas d’autre explication et son emploi dans le cadre d’un modèle d’interaction spatiale enrichi conduirait à sous-estimer la valeur de l’effet de barrière entre les deux républiques.
 
 

autres fonctions d’interaction spatiale
 

 
Si la plupart des phénomènes d’interaction spatiale peuvent être correctement décrit à l’aides des familles de fonction parétienne et exponentielle, il peut arriver que l’on soit amener à recourir à des formes plus complexes. Ainsi, lorsque l’on étudie l’intensité des relations aériennes entre les villes françaises ou européennes, on n’observe pas une fonction monotone de décroissance des relations avec la distance en raison de la concurrence du rail et de la route pour les déplacements à courte et moyenne distance. Il est alors nécessaire d’utiliser une fonction d’interaction spatiale plus complexe qui va croître de 0 à 500-1000 kilomètres puis décroître plus ou moins régulièrement.

D’une manière générale, on peut proposer une généralisation des fonctions parétiennes et exponentielles à l’aide de modèles polynomiaux utilisant soit la distance (modèles exponentiel) soit le logarithme de celle-ci (modèles parétiens).

I_ij = exp [a₀ + a₁.(d_ij) + a₂.(d_ij)²+ ...a_n(d_ij)ⁿ] (fonction exponentielle généralisée)

I_ij = exp [a₀ + a₁.log(d_ij) + a₂.log² (d_ij)+ ...a_n.logⁿ(d_ij)] (fonction parétienne généralisée)

On peut également combiner les deux formes de modèles dans des fonction paréto-exponentielles qui sont en fait l’expression de polynômes combinant distance et logarithmes de la distance dans une fonction complexe …

On ne doit pas perdre de vue que les modèles les plus utiles à l’analyse sont ceux qui comportent un nombre limité de paramètres interprétables et comparables. L’emploi d’une fonction d’interaction spatiale complexe (comportant plusieurs paramètres) n’est donc justifié que si la nature des données empiriques le justifie (Cf. exemple du transport aérien).

4.1.5 Choix de la forme générale du modèle et des contraintes

En se limitant au cas simple où l’on se propose de mettre en relation une matrice de flux homogène avec un unique facteur d’émission, un unique facteur de réception et un unique facteur d’éloignement, on peut définir trois grandes familles de modèles (sans contraintes, à simple contrainte, à double contrainte) et deux cas particuliers (modèles de Wilson et Tobler).

modèle multiplicatif sans contrainte (gravitaire)

 
Les modèles d’interaction spatiale gravitaire correspondent à une classe particulière de modèles multiplicatifs que l’on désigne abusivement sous l’appellation de modèles sans contrainte (unconstrained models) mais qui incorporent en fait le plus souvent une hypothèse de conservation du total général des flux. L’hypothèse générale des modèles de ce type est l’existence d’une relation multiplicative entre les différents facteurs décrivant les capacités d’émission ou de réception des lieux et leur degré d’éloignement. Soit un modèle du type :
 

Modèle multiplicatif "sans contrainte "(conservation du total général)

F*ij = k. f1(Ei) . f2(Rj) . f3(dij)  avec k = [S ij Fij ] / [S ij k. f1(Ei) . f2(Rj) . f3(dij)]

Le paramètre k assure la conservation du total général des flux en imposant que la somme des flux observés (F) soit égale à la somme des flux estimés (F*). Différentes formulations peuvent être proposées selon les hypothèses faites sur les fonctions décrivant l’effet des facteurs d’émission, de réception et d’éloignement. On peut distinguer des modèles gravitaires simples ne comportant qu’un seul paramètre (frein de la distance) et des modèles gravitaires enrichis comportant autant paramètres qu’il y a de facteurs explicatifs (frein de la distance, capacités d’émission, capacités de réception).
 

Modèle gravitaire simple

F*_ij = k. E_i . R_j . d_ij^-a                                            forme parétienne

F*_ij = k. E_i . R_j . exp( -a . d_ij)                   forme exponentielle

Modèle gravitaire enrichi

F*_ij = k. (E_i )b ¹. (R_j)b ² . d_ij^-a                    forme parétienne

F*_ij = k. (E_i )b ¹. (R_j)b ². exp( -a . d_ij)     forme exponentielle

Toutes une série de variantes peuvent être introduites selon le degré de complexité introduit dans les fonctions f₁, f₂, f₃ (nombre de paramètres, forme) et selon le nombre de variables introduites dans chaque sous-ensemble explicatif (émission, réception éloignement).
 

Il n’en demeure pas moins que la caractéristique essentielle de ce type de modèle est de ne faire dépendre l’intensité des flux entre deux lieux que de leurs caractéristiques propres et de ne pas prendre en compte l’influence potentielle des autres lieux et les effets systémiques qui y sont associés.
 
 

modèles multiplicatifs à simple contrainte

 
Les modèles à simple contrainte introduisent une contrainte de conservation des sommes marginales de la matrice des flux qui porte soit sur les flux émis (contrainte de conservation des origines), soit sur les flux reçus (contrainte de conservation des destinations) par chaque lieu. Dans la pratique, ceci revient à supposer connu les sommes originales O ou D et à les utiliser en lieu et place des facteurs d’émission E ou de réception R. Un vecteur de paramètre a₁..a_n (origines) ou b₁…b_n (destinations) permet alors d’assurer la contrainte de conservation des sommes marginales. La forme générale des modèles à simple contrainte est donc la suivante :
 
 

Modèle multiplicatif à simple contrainte de conservation des origines

F*ij = ai . Oi . f2(Rj) . f3(dij)  avec ai = 1 / S j [ f2(Rj) . f3(dij)]


 

Modèle multiplicatif à simple contrainte de conservation des destinations

F*ij = bj . Dj . f1(Ei) . f3(dij)  avec bj = 1 / S i [ f1(Ei) . f3(dij)]

Les modèles à simple contrainte sont les plus utilisés dans les études opérationnelles car ils permettent de modéliser plus précisément les interactions que les modèles sans contraintes, sans pour autant nécessiter une information aussi complète que les modèles à double contrainte. Malgré la symétrie apparente des deux variantes, il existe des différences importantes dans les hypothèses sous-jacentes à ces deux modèles ainsi que dans leurs domaines d’application. Les anglo-saxons les distinguent d’ailleurs sous les appellations de " production-constrained models" et " attraction-constrained models ". (Voir par exemple, Fotheringham & O’Kelly, 1989).

De loin les plus utilisés en recherche opérationnelle (planification urbaine, géomarketing, transports, …), les modèles à simple contrainte sont considérés par de nombreux auteurs comme les plus intéressants en terme de qualité et de quantité d’information restituée. Le choix d’une contrainte portant sur les origines ou sur les destinations n’est pas indifférent : il dépend étroitement de la problématique et de l’information disponible.
 
 

modèle multiplicatif à double contrainte (conservation des origines ou des destinations)

 
Les modèles à double contrainte assurent la conservation simultanée des sommes en lignes et des sommes en colonnes de la matrice des flux. Supposant connue ces sommes en ligne et en colonnes, ils excluent de ce fait la présence de tout autre facteur décrivant les capacités d’émission et de réception des lieux, puisque l’effet de ces derniers serait absorbé par les vecteurs de paramètres a et b qui assurent le respect des contraintes. Estimés de façon itérative (à une constante près) ces vecteurs de paramètres ne peuvent être obtenus de façon analytique et le temps de calcul nécessaire à l’ajustement de modèle à double contrainte est généralement beaucoup plus élevé que pour les modèles sans contraintes ou les modèles à simple contrainte.
 

Modèle multiplicatif à double contrainte de conservation des origines et destinations
 

F*ij = ai . Oi . bj . Dj . f3 (dij)  avec ai = 1 / S j [bj . Dj . f3(dij)] bj = 1 / S i [ai . Oi . f3(dij)] (les deux vecteurs de paramètres étant estimés de façon itérative à une constante près)


 
 
 
 
 
 

Bien qu’ils fournissent en général des ajustements de qualité sensiblement supérieure aux modèles sans contraintes ou aux modèles à simple contrainte, les modèles à double contrainte n’ont en général pas vocation à servir directement d’outil de prévision ou de planification puisqu’ils supposent connu une quantité d’information beaucoup plus élevée que les précédents (la qualité d’ajustement ne faisant que traduire mécaniquement le poids plus important des variables endogènes dans ce type de modèle).
 
 

L’intérêt principal des modèles à double contrainte est l’étude des déterminants de l’interaction spatiale proprement dite, c’est-à-dire du choix des destinations toutes choses égales quant aux capacités d’émission et de réception des lieux. Prenant en compte des effets systémiques (par exemple, le fait que les migrants localisés dans des zones périphériques peuvent être amenés à parcourir en moyenne des distances plus importantes que des migrants localisés dans les zones centrales), ces modèles sont particulièrement utiles lorsque l’on cherche à mettre en évidence l’effet de déterminants spatiaux multiples affectant à des degrés divers le choix des migrants. Nous verrons en particulier dans la seconde partie de ce travail qu’ils permettent de mettre à jour l’existence d’interaction entre des facteurs quantitatifs (distance) et qualitatifs (appartenance territoriale) de localisation géographique.
 
 

Le modèle entropique de Wilson

 
Sans entrer dans les détails de ses présupposés théoriques (entropie), on peut dire que le modèle de Wilson (1967) est une variante des modèles d’interaction spatiale multiplicatifs à double contrainte où la fonction d’interaction spatiale est de type exponentiel et où la valeur du paramètre de frein de la distance est déterminé par l’introduction d’une contrainte supplémentaire de conservation de l’énergie disponible à l’intérieur du système.
 

Modèle multiplicatif à double contrainte de Wilson

F*ij = ai . Oi . bj . Dj . exp( -a . dij) avec ai = 1 / S j [bj . Dj exp( -a . dij)] bj = 1 / S i [ai . Oi exp( -a . dij)] (les deux vecteurs de paramètres étant estimés de façon itérative à une constante près) a est la valeur (unique) du frein de la distance assurant la conservation du coût total de déplacement C définie par : C = S ij [ Fij . dij] = S ij [ F*ij . dij]

L’importance du modèle de Wilson tient moins à ses caractéristiques propres (on peut considérer qu’il s’agit d’un cas particulier de modèle multiplicatif à double contrainte) qu’aux recherches qu’il a suscité et aux fondements théoriques proposés par l’auteur pour lier les états macroscopiques et microscopiques d’un système d’interaction. La discussion de ces questions dépassant toutefois le cadre de cet exposé, nous n’y entrerons pas et renvoyons le lecteur aux très nombreux travaux qui ont été consacrés au modèles de Wilson (voir en particulier la synthèse de Senior, 1979).
 
 

Le modèle additif de Tobler
 
 

Bien qu’il ait suscité peu de recherches, le modèle proposé par W. Tobler est probablement d’une importance théorique aussi grande, si ce n’est plus grande que celui de Wilson. Modèle à double contrainte utilisant une fonction parétienne d’exposant fixe (1/d_ij), le modèle de Tobler présente la particularité d’utiliser une formulation additive dans la définition de la relation entre les facteurs " push " et les facteurs " pull ".
 
 

Modèle additif à double contrainte de Tobler (version originale)

F*ij = (Ai + Bj) / dij avec A et B, deux vecteurs de paramètres estimés à une constante près et assurant la conservation de la somme des flux émis et reçus par chaque unité territoriale et décrivant respectivement les facteurs " push " et " pull ".

 

Cette différence en apparence minime (choix d’une forme additive plutôt que multiplicative) a en fait des conséquences théoriques très profondes qui ont été discutés de façon détaillées par Dorigo & Tobler (1983) et qui donnent au modèle de Tobler des propriétés remarquables, notamment en ce qui concerne la question de la désagrégation des matrices de flux en unité spatiales de tailles de plus en plus réduites et l’établissement de représentations cartographiques des champs de transfert (analyse de la composante dissymétrique des flux).

Malheureusement ce modèle demeure à ce jour peu étudié et la plupart des auteurs de manuel sur l’interaction spatiale se contentent d’un coup de chapeau rituel aux qualités intrinsèques du modèle de Tobler, sans chercher véritablement à en approfondir les hypothèses et à les confronter à celles des modèles d’interaction de type multiplicatif.

4.1.6. : Choix du critère d'ajustement et détermination des paramètres à estimer

En se limitant au cas simple où le modèle comporte un seul paramètre à estimer (le frein de la distance ou de la fonction de côut généralisé), nous allons discuter quelques solutions proposés pour déterminer la valeur optimale du paramètre et mesurer la qualité d'ajustement globale d'un modèle d'interaction spatiale

Les solutions statistiques classiques fondées sur la linéarisation

Les solutions statistiques classiques au problème de l'ajustement consistent à se ramener à un problème d'ajustement linéaire ou non-linéaire fondé sur le critère des moindres carrés.

Si l'on prend l'exemple du modèle multiplicatif sans contrainte dans sa variante gravitaire enrichie (Cf. 4.1.3) on voit que la transformation logarithmique permet d'écrire l'équation sous la forme d'un modèle de régression linéaire :

ln(F*_ij )= ln(k) + b ₁.ln (E_i ) + b ₂. ln(R_j) + a .(d_ij )         forme exponentielle
ln(F*_ij )= ln(k) + b ₁.ln (E_i ) + b ₂. ln(R_j) + a . ln(d_ij )     forme parétienne

Le critère de minimisation (implicite) est alors la somme des différences élevées au carré entre les logarithmes des flux observés et des flux estimés, la qualité de l'ajustement étant mesurée par le coefficient de détermination de la régression multiple.

Si l'on souhaite utiliser un modèle gravitaire simple (sans exposant sur les facteurs d'émission et de réception, on peut également utiliser une autre transformation qui amène à une équation de régression simple :

ln[F*_ij /(E_i . R_j)]= ln(k) + a .(d_ij )         forme exponentielle
ln[F*_ij /(E_i . R_j)]= ln(k) + a. ln(d_ij )     forme parétienne

Le critère de minimisation est alors différent puisqu'il s'agit de la minimisation non plus du logarithme des flux mais du logarithme de l'intensité des flux (définie comme le rapport entre le flux observé et le produit des capacités d'émission et de réception).

Ces deux solutions ont l'avantage d'une très grande simplicité de mise en oeuvre et autorisent toute une série d'enrichissements du modèle (il est fracile d'introduire plusieurs facteurs explicatifs d'émission, de réception ou d'éloignement si leurs effets sont supposés multiplicatifs), mais elles achoppent sur plusieurs difficultés pratiques et théoriques qui conduisent actuellement à leur abandon par la plupart des spécialistes des modèles d'interaction spatiale :

1- Les flux nuls ne peuvent pas être introduits dans des modèles de ce type (le logarithme de 0 n'étant pas défini) et il faut opter pour une solution arbitraire consistant soit à les retirer de l'analyse, soit à leur donner une valeur minimum.
2- La contrainte de conservation du total des flux n'est plus assurée par le paramètre k (puisque la minismisation se fait sur le logarithme des flux ou de leur intensité et non pas sur les flux eux-mêmes) ce qui oblige à une correction ex post du modèle et qui introduit une nouvelle forme d'arbitraire.
3- La minimisation sur le logarithme des flux (ou de leur intensité) conduit à accorder une importance considérable aux petits flux dans l'ajustement du modèle, alors que les flux de faibles intensité sont ceux pour lesquels l'incertitude de mesure est la plus forte. On risque alors d'obtenir une mauvaise estimation des flux les plus importants (ce qui est gênant dans le cadre d'un modèle de prévision) et de subir des biais liés à la présence de points-individus exceptionnels (sans parler des problèmes d'autocorrélation et d'hétéroscédasticité des résidus).
4- les modèles de régression logarithmique ne sont applicables facilement qu'au cas des modèles sans containte mais ils sont beaucoup plus difficile à mettre en oeuvre pour la réalisation de modèles à simple ou double contraintes.

Au total, les ajustements par régression log-linéaire constituent aujourd'hui une étape dépassée et des méthodes équivalentes mais beaucoup plus puissantes (régression poissonnienne) constitue des alternatives beaucoup plus puissantes et tout aussi faciles d'emploi.
 

L'approche heuristique de M. Poulain (critère du Chi-2)

Bien qu'elle soit davantage heuristique que statistique, l'approche suggérée par M. Poulain au début des années 1980 a constitué une étape importante et toujours d'actualité dans les recherches sur l'ajustement des modèles d'interaction spatiale.

Partant d'une observation empirique sur les mouvements migratoires en Belgique, M. Poulain avait constaté qu'il était possible d'estimer l'ordre de grandeur de l'incertitude de mesure des flux migratoires en comparant deux sources différentes : celle fournie par le lieu de destination et celle fournie par le lieu d'origine des migrants. La Belgique est en effet un pays doté d'un registre de migration, de sorte que tout déplacement est enregistré à la fois au lieu de départ et au lieu d'arrivée. Ainsi, le flux Anvers-Bruxelles peut-être connu soit par le dépouillement du registre des migrants qui ont déclaré leur départ d'Anvers, soit par le dépouillement du registre des migrants qui ont déclaré leur arrivée à Bruxelles. Or, il existe de nombreux cas de non-coïncidence entre les deux flux puisqu'un migrant peut changer d'avis après avoir fait sa déclaration ou bien peut effectuer une déclaration fausse ou imprécise. Il arrive ainsi fréquemment qu'un migrant se déplaçant vers une commune de banlieue d'une grande ville n'indique pas cette commune précise mais le nom de la ville-centre dont elle dépend.

La comparaison d'un échantillon de flux décrits par les deux sources a permis à M. Poulain d'établir que les différences entre les deux sources étaient proportionnelles au racine carré de la valeur du flux, ce qui est un résultat classique mais important puisqu'il indique que l'erreur relative est de son côté inversement proportionnelle à la racine carrée de la taille du flux (un flux de 4 personnes sera connu avec une incertitude 2 fois plus forte qu'un flux de 16 personnes).

Partant de ce résultat (dont il faudrait examiner s'il est généralisable à d'autres types de flux), M. Poulain a conclu que le critère d'ajustement le plus logique était celui qui ferait jouer aux flux un rôle inversement proportionnel à leur erreur de mesure, ce qui revient au vu des résultats empiriques à utiliser le critère de minimisation du chi-deux de la différence entre flux observés et flux estimés. L'erreur du modèle est donc définie par la somme du chi-2 de l'erreur sur chacun des flux observés et estimés :

ERR(Mod) =  S _ij [(F_ij - F*_ij)²/F*_ij]

Pour exprimer la qualité d'ajustement sous la forme d'un coefficient de détermination variant entre 0 et 1, on peut définir une erreur maximale correspondant à un modèle de référence. M. Poulain utilise comme référence le modèle de flux moyen qui est bien adapté au cas des modèles sans contraintes mais qui serait plus discutable dans le cas de modèles à simple ou double contrainte.

ERR(Max) =  S _ij [(F_ij - F)²/F]     avec F = moyenne des flux

La qualité d'ajustement est alors définie comme la part de l'incertitude initiale (erreur maximale) qui a été réduite par le modèle utilisée :

AJU (Mod, Max) = [ERR(Max) - ERR(Mod)] / ERR(Max)

Plus généralement, lorsque l'on introduit successivement plusieurs variables explicatives (1,2,...z) dans un modèle d'interaction spatiale (modèles 1, 2, ...z) on peut peut mesurer la contribution relative de l'ajout d'une variable supplémentaire à la réduction de l'incertitude non prise en compte par les modèles précédents :

AJU (k) = [ERR(Mod_k-1) - ERR(Mod_k)] / ERR(Mod_k-1)

Ainsi, si l'on veut mesurer les apports respectifs des masses et de la distance dans un modèle de type gravitaire on définira trois modèles successifs correspondant à l'absence de variable explicative (Mod0), à la présence des masses (Mod1) et à la présence des masses et de la distance (Mod2). Et on calculera les coefficients d'ajustement correspondant aux passages successifs du modèle 0 au modèle 1 (pouvoir explicatif des masses) puis du modèle 1 au modèle 2 (pouvoir explicatif de la distance toutes choses égales quant aux masses) et pas simplement du modèle 0 au modèle 2 (pouvoir explicatif conjoint des masses et de la distance).
 

Les solutions statistiques modernes : maximisation de l'entropie et régression poissonienne

Dans une perspective plus théorique que celle proposée par M. Poulain, de nombreux auteurs ont cherché à fonder le choix du critère d'ajustement sur la nature du processus générateur des flux, ce qui est la solution la plus satisfaisante puisqu'elle permet (en théorie) d'adapter le choix du critère à la nature probabiliste du phénomène considéré.

Si la première approche de ce type revient aux travaux de Wilson sur la maximisation de l'entropie sous contrainte, elle a depuis lors été généralisée par des auteurs tels que Fotheringham & O Kelly (1989) et surtout dans l'ouvrage de référence de Sen & Smith (1995). La solution proposée par Wilson correspond en effet à un corpus particulier d'hypothèse sur la distribution des flux, issu d'une analogie avec la physique, qui n'est pas nécessairement vérifié dans les situations concrètes d'application des modèles d'interaction spatiale. La notion d'entropie et les travaux équivalents de la synergétiques se fonde sur l'hypothèse non nécessairement vérifiée que la probabilité macroscopique d'état du système dépend de la distribution la plus probable des micro-états de celui-ci. Or cette hypothèse n'est valide que si le processus générateur des flux est de type poissonien, sans effets d'agrégation (ensemble de flux liés à une même date) ou d'autocorrélation temporelle (influence des flux passés sur les flux futurs).

La solution proposée par Wilson revient dans la pratique à l'ajustement d'un modèle de régression poissonienne selon le critère du maximum de vraisemblance (Flowerdew) mais elle constitue un cas particulier d'un corpus plus général de solution où la distribution des flux pourrait dépendre d'un processus générateur quelconque et suivre d'autres lois que la loi de Poisson (par exemple une loi binomiale négative). Des recherches sont en cours (Calzada C., d'Aubigny G., Grasland C., Viho G., Vincent J.M.) pour mettre au point de nouveaux outils d'ajustement adaptés à ces hypothèses et vérifier leur adéquation sur des données empiriques.

Sans entrer dans plus de détail on notera que les approches statistiques modernes fondées sur la régression poissonienne (ou ses variantes) et le critère du maximum de vraisemblance présentent des avantages certains par rapport aux méthodes antérieures :

1- L'introduction des contraintes (simple, double) est une simple conséquence du choix des variables explicatives introduites dans le modèle, c'est-à-dire de l'information disponible. Elle est donc beaucoup plus naturelle et beaucoup plus claire.
2- L'examen de la réduction de la déviance en fonction du nombre de facteurs explicatifs introduits dans le modèle permet d'assigner à chaque paramètre un niveau de significativité partiel, analogue aux coefficients de régression multiples. On peut donc déterminer quelles variables explicatives jouent un rôle significatif dans l'explication du phénomène et lesquelles doivent être retirées. Elle permet également de déterminer si le modèle est "complet", c'est-à-dire si des variables latentes restent à découvrir ou non.
3- La (relative) simplicité de la technique de régression poissonnienne permet d'ajuster des modèles complexes où les déterminants de l'interaction sont multiples et où leurs effets respectifs sont contrôlés réciproquement. On peut donc mesurer l'effet de chaque facteur explicatif (distance, capacités d'émission ou de réception) toutes choses égales quant à celui des autres, ce qui est extrêmement utile d'un point de vue théorique et d'un point de vue pratique (Cf. Bröcker & Rohweder).
 
 
 

 

Suite du chapitre