|
RELATIONS DANS LE TEMPS ET DANS L'ESPACE Claude Grasland
|
![]() Cours
Cours ![]() Exercices
Exercices ![]() Bibliographie
Bibliographie ![]() Menu précédent
Menu précédent
![]()
PLAN DU CHAPITRE 1
- Analogie entre distribution spatiale et distribution statistique
- Signification spatiale des valeurs centrales et paramètres de dispersion
2.2 ) Mesures de position et de dispersion dans un espace bidimensionnel
- Mesures de position (localisation du point le plus accessible)
- Mesures de dispersion spatiale (distance au point le plus accessible)
2. DETERMINATION DU CENTRE DE GRAVITE (Point moyen)
2.2 ) Calculs sans pondération
2.2 ) Calculs avec pondération
3.1 ) Détermination du point médian
3.2 ) Détermination de la dispersion autour du point médian
4.1) Calcul des points modaux à l'aide d'un maillage territorial
4.2) Calcul des points modaux sans maillage territorial
DOCUMENT 1 : CONSTRUCTION D'UNE DISTRIBUTION SPATIALE UNIDIMENSIONNELLE
(a) Distribution spatiale à une seule dimension
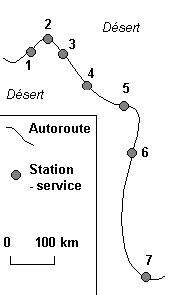
(b)Tableau de position
|
Station n° |
Position par rapport à la station n°1 |
Position par rapport à la station n°4 |
|
1 |
0 |
-200 |
|
2 |
50 |
-150 |
|
3 |
100 |
-100 |
|
4 |
200 |
0 |
|
5 |
300 |
100 |
|
6 |
400 |
200 |
|
7 |
700 |
500 |
(c) Représentation graphique unidimensionnelle
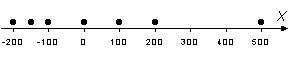
PROBLEME :
Calculez les paramètres statistiques de cette distribution. Quelle signification spatiale peut-on leur donner ?
Paramètre Valeur Signification
Centre* : …………. : …………………………………………………………..
Moyenne : …………. : …………………………………………………………..
Médiane : …………. : …………………………………………………………..
Mode : …………. : …………………………………………………………..
Etendue : …………. : …………………………………………………………..
Ecart-type : …………. : …………………………………………………………..
Ecart abs. moyen : …………. : …………………………………………………………..
Ecart abs. médian** : …………. : …………………………………………………………..
* : (maximum+minimum)/2
** : moyenne des ecarts à la médiane en valeur absolue.
DOCUMENT 2 : MESURES DE CENTRALITE ET D'ACCESSIBILITE DANS UN ESPACE UNIDIMENSIONNEL
(a) Distribution spatiale unidimensionnelle pondérée
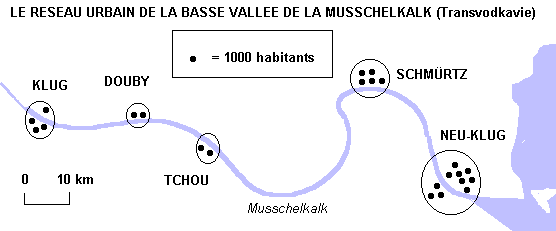
La Musschelkalk est navigable de Klug jusqu'à son embouchure où se trouve le port de Neu-Klug. Où faut-il localiser un dépôt de marchandise permettant de desservir le mieux possible les habitants des 5 villes de la basse vallée de la Musschelkalk ?
(b) Tableau statistique associé
|
Ville |
Distance à la mer |
Population |
|
I |
Xi |
Pi |
|
NEU-KLUG |
0 |
10000 |
|
SCHMÜRTZ |
30 |
5000 |
|
TCHOU |
80 |
2000 |
|
DOUBY |
100 |
2000 |
|
KLUG |
120 |
6000 |
(c) Déterminez la position du dépôt central et son accessibilité en vous servant :
Du centre et de l'étendue
De la moyenne et de l'écart absolu moyen
De la médiane et de l'écart absolu médian
De la moyenne pondérée et de l'écart absolu moyen pondéré
De la médiane pondérée et de l'écart absolu médian pondéré
Quelle combinaison de paramètres est la plus satisfaisante ?
DOCUMENT 3 : DETERMINATION DU CENTRE DE GRAVITE D'UNE DISTRIBUTION SPATIALE
(a) L'exemple des élections en Transvodkavie
Georges W. Goret est candidat à l'élection présidentielle de Transvodkavie. Il doit tenir un meeting dans la capitale, Trifouillesky, où il est attendu par 150 militants répartis en 9 comités de soutien. Les rues de la ville de Trifouillesky sont organisées selon un plan en damier.
Où Georges W. Goret doit-il localiser son meeting s'il veut satisfaire le plus de comités de soutien ? le plus de militants ?
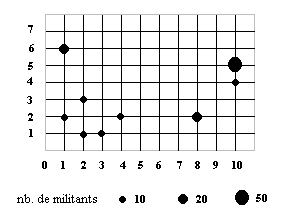
(b) calcul du point moyen (sans pondération)
Si Georges W. Goret veut satisfaire le maximum de comités de soutien,
il considère que chaque comité a la même importance, quel que soit le nombre
de militants. Il va donc procéder à des calculs non pondérés pour
trouver le point moyen et la dispersion autour de ce point moyen. Les formules
de calcul seront alors les suivantes
(c) calcul du point moyen (avec pondération)
Si Georges W. Goret veut satisfaire le maximum de militants, il considère que les comités n'ont pas la même importance. Chaque comité a une importance proportionnelle à son nombre de militants. Il va donc procéder à des calculs pondérés pour trouver le point moyen et la dispersion autour de ce point moyen.
(d) Exemple de calcul du point moyen : les élections en Transvodkavie
|
Comité |
X |
Y |
P |
XP |
YP |
(X-mX)2 |
(Y-mY)2 |
P.(X-mXp)2 |
P.(Y-mYp)2 |
|
1 |
1 |
2 |
10 |
10 |
20 |
12.6 |
0.8 |
250 |
25.6 |
|
2 |
1 |
6 |
20 |
20 |
120 |
12.6 |
9.7 |
500 |
115.2 |
|
3 |
2 |
1 |
10 |
20 |
10 |
6.5 |
3.6 |
160 |
135.2 |
|
4 |
2 |
3 |
10 |
20 |
30 |
6.5 |
0.0 |
160 |
7.2 |
|
5 |
3 |
1 |
10 |
30 |
10 |
2.4 |
3.6 |
90 |
202.8 |
|
6 |
4 |
2 |
10 |
40 |
20 |
0.3 |
0.8 |
40 |
102.4 |
|
7 |
8 |
2 |
20 |
160 |
40 |
11.9 |
0.8 |
80 |
409.6 |
|
8 |
10 |
4 |
10 |
100 |
40 |
29.6 |
1.2 |
160 |
16.0 |
|
9 |
10 |
5 |
50 |
500 |
250 |
29.6 |
4.5 |
800 |
980.0 |
|
total |
41 |
26 |
150 |
900 |
540 |
112.2 |
24.9 |
2240 |
1994 |
DOCUMENT 4 : DETERMINATION DU POINT LE PLUS ACCESSIBLE D'UNE DISTRIBUTION SPATIALE (point médian)
La détermination du point médian n'est pas facile en distance euclidienne (déplacements possibles dans toutes les directions de l'espace). Elle est en revanche très simple en distance rectilinéaire (déplacements possibles uniquement selon deux axes orthogonaux).
Le point médian non pondéré est le point M minimisant la somme des distances à tous les points
Propriété : est minimum si j =M
Les paramètres de dispersion associés sont les quantiles DM,% de la distribution des points en fonction de la distance au point médian.
Ex. La distance médiane DM,50% est le rayon du cercle centré sur le point médian M permettant de rassembler 50% des points de la distribution.
(b) Point médian (pondéré)
Le point médian pondéré est le point MP minimisant les distances à l’ensemble de la population P
Propriété : est minimum si j = MP
Les paramètres de dispersion associés sont les quantiles DM,P% de la distribution de la population en fonction de la distance au point médian
Ex. La distance médiane pondérée DM,P50% est le rayon du cercle centré sur le point médian M permettant de rassembler 50% de la population P.
(c) Exemple de calcul du point médian : les élections en Transvodkavie
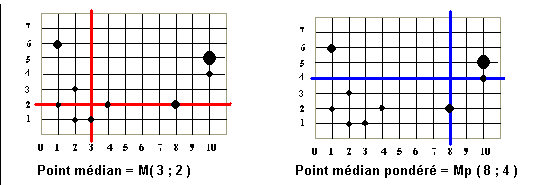
DOCUMENT 5 : DETERMINATION DES PICS DE CONCENTRATION D'UNE DISTRIBUTION SPATIALE (points modaux)
(a) détermination des points modaux à l'aide d'un maillage territorial
Le cas unidimensionnel
Dans le cas d'une distribution statistique (ou d'une distribution spatiale
unidimensionnelle) , le mode correspond au centre de la classe
qui a la fréquence moyenne (effectif/ amplitude) la plus élevée, c'est-à-dire
à la zone de la distributions où les valeurs sont le plus concentrées.
Si l'histogramme comporte plusieurs "pics" séparés par des "creux", la distribution
est multimodale.
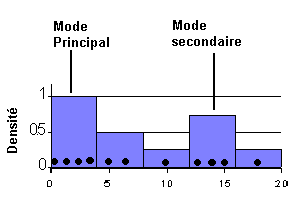
Le cas bidimensionnel
Dans le cas d'une distribution spatiale (bidimensionnelle), les classes correspondent à des unités territoriales, l'amplitude correspond à la surface et la fréquence moyenne à la densité spatiale (effectif/surface). Les points modaux correspondent alors aux pics de densité séparés par des espaces moins denses.
| Distribution spatiale |
Effectifs |
Densité |
On remarque que le nombre de points modaux et leur position varie en fonction du découpage territorial
(b) détermination des points modaux sans maillage territorial (lissage)
Pour éviter les inconvénients liés aux différences forme ou de taille des unités spatiales, on peut recourir à des méthodes de lissage pour trouver les points nodaux. Ces méthodes sont très nombreuses.
La méthode la plus simple consiste à utiliser une fenêtre mobile avec un diamètre fixé par l'utilisateur :
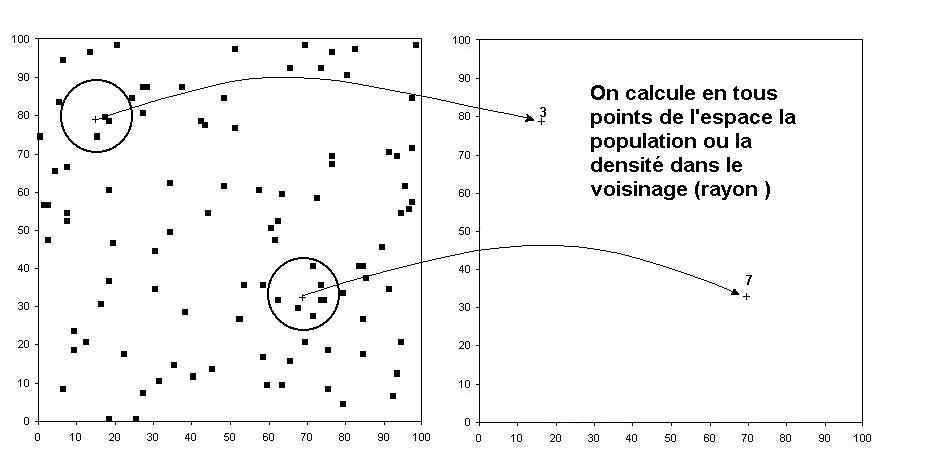
On obtient alors une carte lissée de la densité de population dans le voisinage en corrigeant les effets de bordure
|
Densité dans le voisinage = |
population du voisinage / |
surface du voisinage |
Le degré de généralisation est plus ou moins important selon le rayon de lissage choisi :
|
Densité dans un voisinage de 10 |
Densité dans un voisinage de 20 |
|
|
|
|
|
![]()
![]()