Cours     Exercices  Bibliographie  Menu précédent

Documents de cours

PLAN DU CHAPITRE 2

1. Paramètres de dispersion relative

• Formules de calcul
• Avantages et inconvénients

2. Indice d'équirépartition de Hoover

• Formules de calcul
• Avantages et inconvénients

3. Courbe de Lorenz et indice de Gini

• Formules de calcul
• Avantages et inconvénients

4. Problèmes d'agrégation

• Instabilité des indices en fonction du niveau d'agrégation
• Raisons de cette instabilité.

DOCUMENT 1 : LA MESURE DES INEGALITES ECONOMIQUES

On considère une ressource R partagée entre différents individus 1..i…p formant une population P. Chaque individu i possède une quantité de ressource notée R_i . On suppose que les individus sont classés par ordre de revenus croissants (R₁ < .. < R_i < … < R_p ) ce qui signifie que R₁ est la quantité de ressource de l'individu le plus pauvre et R_p la quantité de ressources de l'individu le plus riche. On pose les définitions suivantes :

R_tot = R₁+ .. + R_i + .. +R_p : quantité totale de ressources disponibles

R_moy = R_tot/p : quantité moyenne de ressource par individu

f_i = R_i/R_tot : proportion de la ressource totale détenue par l'individu i

f_moy = 1/p : proportion moyenne de richesse détenue par un individu.

• La répartition la plus égalitaire possible
correspond au cas où tous les individus disposent exactement de la même quantité de ressource, soit :

R₁ = ... = R_i = ... = R_p ou (ce qui revient au même) f₁ = … = f_i = … f_p

• La répartition la plus inégalitaire possible correspond au cas où un individu dispose de la totalité de la ressource et où tous les autres individus n'en possèdent pas du tout, soit :

f₁ = … = f_i = … f_p-1 = 0 et f_p=1

PROBLEME : Comment définit un indice qui mesure la concentration de la ressource à l'aide d'une valeur comprise entre 0 (répartition la plus égalitaire possible) et 1 (répartition la plus inégalitaire possible).

Le coefficient de variation des revenus (écart-type/ moyenne) permet de fournir un premier indice de concentration. On peut également utiliser l'intervalle interquartile relatif ((Q3-Q1)/médiane) ou tout autre rapport entre un paramètre de dispersion et une valeur centrale.

• Avantage
: L'unité de mesure est éliminée (paramètre exprimé en % de variation) ce qui permet des comparaisons entre différentes ressources (revenus, culture, terres, …) , différents échantillons, etc.
• Inconvénient : La valeur 0 correspond bien à l'absence de concentration (équirépartition) mais l'indice peut être supérieur à 1 et n'a pas de borne supérieure correspondant à la concentration maximale (Ex. Moyenne = 1000 $ et écart-type = 2500 $ => C.V. = 2.5 ou 250%).

2eme solution : Calcul de l'indice d'équirépartition de Hoover (I)

L'indice d'équirépartition de Hoover indique la quantité de ressource qu'il faudrait transférer d'un individu à un autre pour aboutir à l'équirépartition :

Indice de Hoover  = 1/2 Somme_i |  f_i - f_moy|

• Avantage : L'indice est bien compris entre 0 (équirépartition) et 1 (concentration maximale). On notera que la valeur 1 ne pourrait être atteinte que si on avait une infinité d'individus ne possédant rien et un individu possédant tout.
• Inconvénients :
L'indice ne renseigne pas sur la structure des inégalités (2 groupes à revenus différents ou bien 1 individu très riche et beaucoup d'individus pauvres).

La courbe de Lorenz C(x,y) est fondée sur le cumul simultané de la population (x) et des revenus (y) en allant des individus les plus riches aux individus les plus pauvres. Elle permet de répondre à des questions du type : "Quel est le % (y) des revenus est détenu par un certain % (x) des individus les plus pauvres". Elle est généralement établie à partir d'une répartition de la population par déciles :

Source : Enfant & Familles : http://www.cfc-efc.ca/docs/00000513.htm

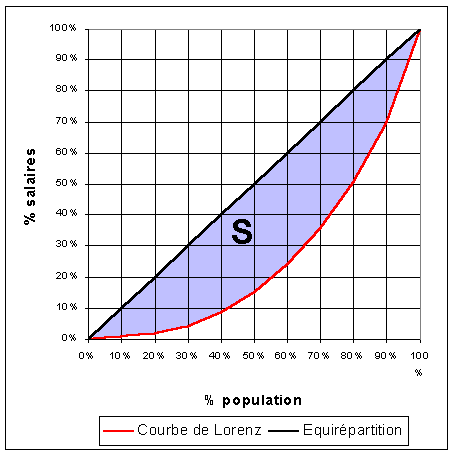
La courbe de Lorenz appliqué au cas des salaires des ménages canadiens permet par exemple de montrer que :

• Les 50% les plus pauvres ne disposent que de 15% du revenu total
• 50 % des revenus sont détenus par les 20% des ménages les plus riches

L'indice de Gini se déduit de la courbe de Lorenz en calculant la surface de concentration S comprise entre celle-ci et la droite d'équirépartition. Cette surface S est au maximum de 0.5 (si un individu concentre tous les revenus et si une infinité d'individus n'a rien) donc pour obtenir un indice compris entre 0 et 1 on pose :

Indice de Gini = 2 S

On peut calculer la surface de concentration (et donc l'indice de Gini) à l'aide du tableau donnant les ressources cumulées (y_i) en fonction des population cumulée (x_i) en utilisant la formule suivante :

• Avantage
: L'indice de Gini est bien compris entre 0 (équirépartition) et 1 (concentration maximale). Il est complété par la courbe de Lorenz qui apporte des informations plus précises.
• Inconvénient
: Plus abstrait que l'indice de Hoover. Ne possède pas de signification concrète.

Problème : Essayons de transposer les indices de concentration économique au problème de la concentration des terres par des agriculteurs. On prend l'exemple fictif d'une région pionnière comportant 1600 hectares partagés entre 16 fermes.

Dans le Tableau 1, on possède toutes les informations au niveau des fermes.

Dans le Tableau 2, les résultats sont agrégés par communes.

Dans le Tableau 3, les résultats sont agrégés par canton.

L'étendue de la distribution passe de 695 au niveau des fermes à 100 au niveau des communes et 0 au niveau des cantons

Le coefficient de variation qui mesure plus précisément les différences relatives passe de 161% au niveau des fermes à 40% au niveau des communes et 0% au niveau des cantons.

• Les différences de taille moyenne des fermes (par canton ou par communes) ne reflètent donc pas du tout les différences de taille réelle entre les fermes. L'agrégation permet généralement de dissimuler les inégalités si chaque zone comporte des fermes de grande taille et de petite taille.

Au niveau des fermes, l'indice de Hoover est de 0.438, ce qui indique qu'il faudrait redistribuer 44 % des terres pour que toutes les fermes aient la même superficie.

Au niveau des communes, l'indice de Hoover n'est plus que de 0.188, ce qui indique qu'il suffirait de transférer 18% des terres d'une commune à une autre pour que chaque commune dispose de la même quantité moyenne de terre / ferme.

Au niveau des cantons, l'indice de Hoover est de 0, ce qui indique que chaque canton dispose de la même quantité moyenne de terre / ferme.

• L'équirépartition qui peut exister à un certain niveau d'agrégation
(ex. le % de ferme et le % de terres sont identiques au niveau des cantons) ne préjuge pas de l'inégale répartition qui peut exister au niveaux inférieurs d'agrégation, et en particulier au niveau des individus. Le problème est le même avec l'indice de Gini.

Exercices

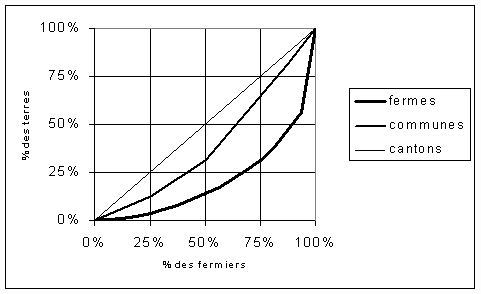
 EXERCICE D'APPLICATION

Carte de localisation

Regroupez les individus en trois zones et recalculez les indices. Vous pouvez choisir soit de dissimuler les inégalités, soit de les mettre en évidence.