|
Analyse spatiale et modélisation des phénomènes géographiques Claude Grasland Université Paris VII / UFR GHSS - Licence de Géographie / Année 2000-2001 / 1er Semestre
|
B.1) Distribution des densités par rapport à un point
B.3) Distribution des densités par rapport à une surface
C. ANALYSE DE LA FORME D’UNE DISTRIBUTION
C.1) Formes et processus générateurs des distributions
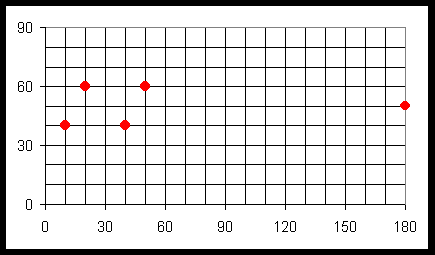
Document 1 : Transformation de coordonnées en matrice de distance
Tableau des coordonnées
| i | Xi | Yi |
|
1
|
20
|
60
|
|
2
|
50
|
60
|
|
3
|
10
|
40
|
|
4
|
40
|
40
|
|
5
|
180
|
50
|
Carte de localisation

Matrice des distances euclidiennes :
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrice des distances rectilinéaires :
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrice des distances orthodromiques :
On suppose que X est la longitude en degrés et Y la latitude en degrés :
DOij=6368*Arccos[(sin(Yi).sin(Yj))+(cos(Yi).cos(Yj).sin(Xi).sin(Xj))+cos(Xi).cos(Xj)]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Document 2 : Définition et formule de calcul des points centraux et des paramètres de dispersion associé
a) Point moyen (non pondéré)
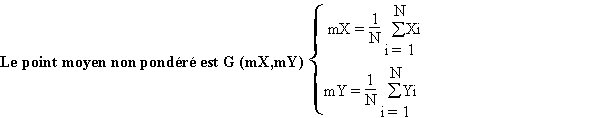
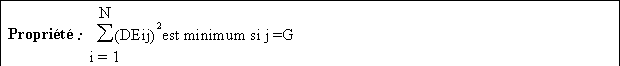
Le paramètre de dispersion associé est la distance-type sD qui est la racine carré de la moyenne du carré des distances, c’est-à-dire la racine carrée de la somme des variances de X et de Y.
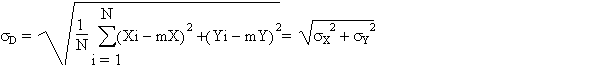
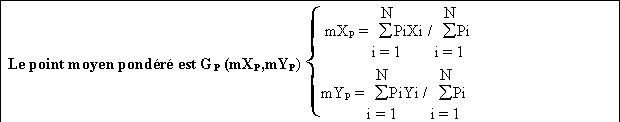

Le paramètre de dispersion associé est la distance-type pondérée sD,P qui est égale à la racine carrée de la moyenne du carré des distances à tous les membres de la population P. Si on note sX,P l’écart type de X pondéré par P et sY,P l’écart type de Y pondéré par P, on a :
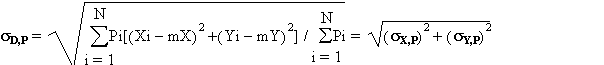
Le point médian non pondéré est le point M minimisant la somme des distances à tous les points

Les paramètres de dispersion associés sont les quantilesDM,% de la distribution des points en fonction de la distance au point médian.
Ex. La distance médiane DM,50% est le rayon du cercle centré sur le point médian M permettant de rassembler 50% des points de la distribution.
Le point médian pondéré est le point MP minimisant les distances à l’ensemble de la population P
![]()
Les paramètres de dispersion associés sont les quantiles DM,P% de la distribution de la population en fonction de la distance au point médian
Ex. La distance médiane pondérée DM,P50% est le rayon du cercle centré sur le point médian M permettant de rassembler 50% de la population P.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Document 3 : Exemples d’utilisation du point moyen et de la distance-type
(a) Déplacement du point moyen de population en Iowa (1850-1970)
(b) Evolution de la distance-type en Iowa (1850-1970)
(c) Calcul des centres de gravité de différentes productions en Ukraine vers 1926
Document 4 : Analyse d’une distribution en fonction de la distance à un point de référence.
(a) Distribution de la population de Yaoundé en fonction de
la distance au centre en 1987
|
|
Surface | Population en 1987 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N.B. Les calculs sont effectués à l’aide du centroïde des chefferies : c’est pourquoi la croissance des surfaces n’est pas régulière.
(b) Forme de la décroissance de la densité de population en fonction de la distance au centre à Yaoundé en 1987
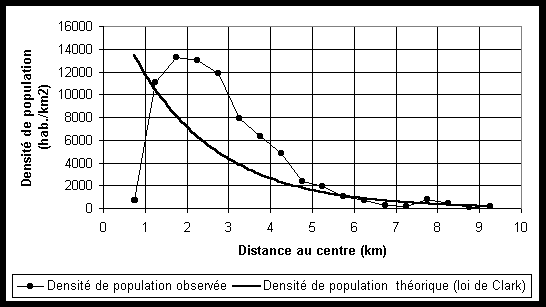
Source : Bopda A., 1997, Yaoundé dans la construction nationale au Cameroun : territoire urbain et intégration, Thèse, Université Paris 1, 2 vol.;
Document 5 : Test de la forme d’une distribution
(a) forme d’une distribution de points
(2) la position d’un point nouveau est indépendante de la position des points précédents
(2) la localisation d’un premier point favorise l’apparition d’autres points à proximité
(2) la localisation d’un premier point défavorise l’apparition
d’autres points à proximité
(b) Méthode des quadrats
(1) Soit un semis de N points distribués sur un espace E
(2) On recouvre l’espace E d’un ensemble de K mailles de formes régulières. Le nombre moyen de points par maille est égale à D=N/K
(3) On associe à chaque maille i le nombre Di de points qu’elle contient, puis on calcule la variance du nombre de points par maille V(D) et on en déduit l’indice de concentration
IC=V(D)/D
IC» 1 : distribution aléatoire (loi de Poisson)
IC>1 : distribution plutôt concentrée
IC<1 : distribution plutôt régulière
(4) On dénombre les nombre de mailles en fonction du nombre de points qu’elles contiennent. On note K(n) le nombre de mailles comportant n points.
(5) On détermine les effectifs théoriques K*(n) qui seraient obtenus si la distribution était aléatoire à l’aide de la formule suivante :
![]()
(6) On teste l’égalité des deux distributions K(n) et
K*(n) à l’aide d’un test du Chi-2. En fonction des résultats
du test on conclue au caractère aléatoire ou non aléatoire
de la distribution observée.
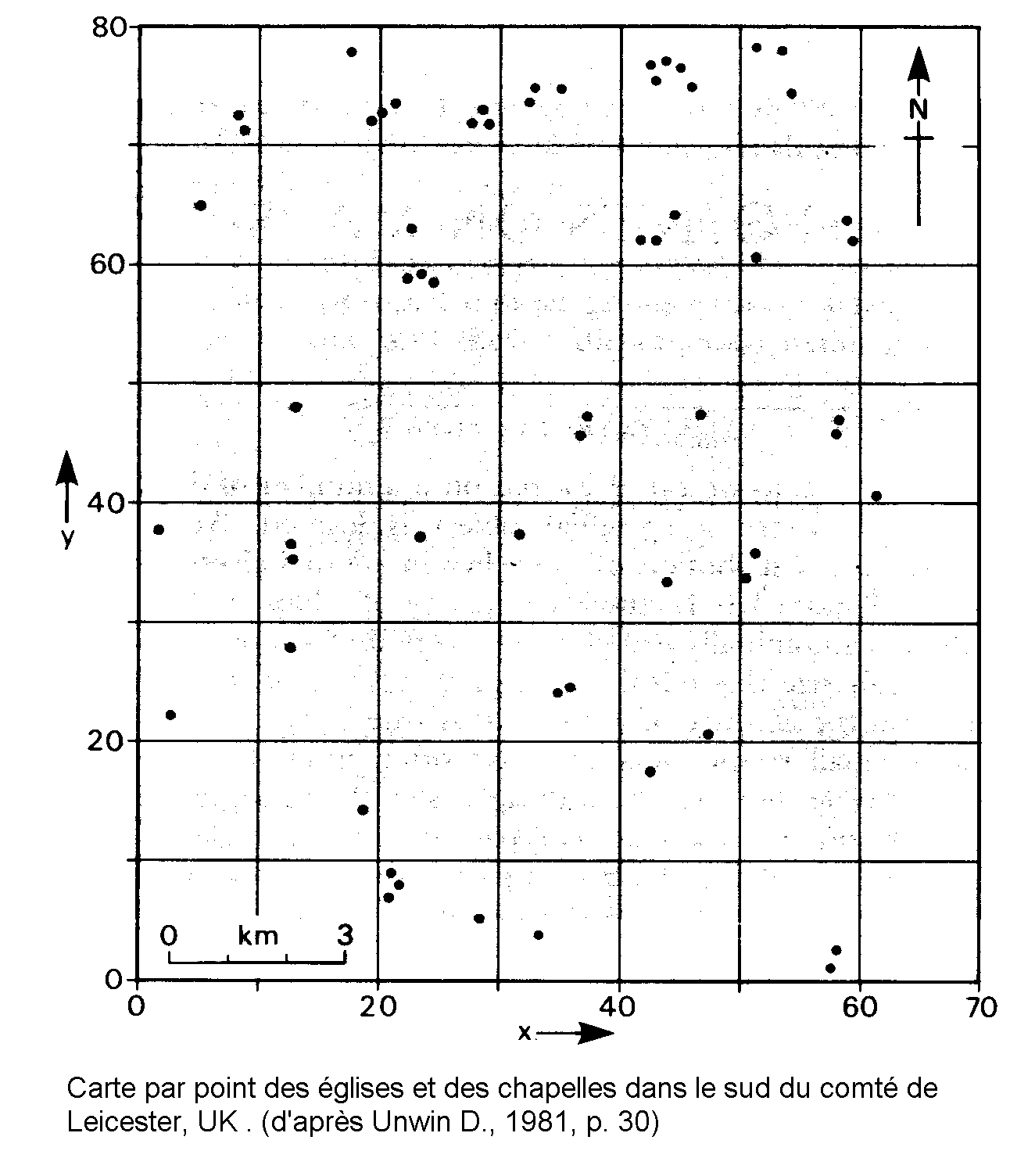
(c) Exemple d’application de la méthode des quadrats
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Densité moyenne D = nb. de points / nb. de quadrats = 60/56 = 1.071 | ||||
| Variance V(D) = 93.714 / 55 = 1.704 | ||||
| Indice de concentration IC = V(D)/D= 1.590 | ||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
| Nombre de degrés de liberté = nb. de classes -1 = 4-1=3 | ||||||
| Chi2 (3, 0.01) = 11.34 | ||||||
| Chi2 (3, 0.05) = 7.82 | ||||||
| Chi2 (3, 0.10) = 6.25 | ||||||
| Chi2 (3,0.20) = 4.64 | ||||||
(1) Soit un semis de N points distribués sur un espace de surface S. On note d la densité moyenne de points par unité de surface à l’intérieur de l’espace considéré (d=N/S)
(2) On calcule pour chaque point i la distance Dmin(i) qui le sépare de son voisin le plus proche.
(3) On calcule ensuite la moyenne des distances observées au plus proche voisin DO
(4) On détermine la distance théorique moyenne au plus proche voisin DT dans le cas d’une distribution aléatoire à l’aide de la formule :
![]()
(5) On calcule l’indice de dispersion qui est le rapport entre ces deux distances :
R=DO/DT
(6) On peut enfin tester le caractère aléatoire de la
distribution à l’aide d’un test paramétrique (Cf. manuels
d’analyse spatiale).
Signification des valeurs de R
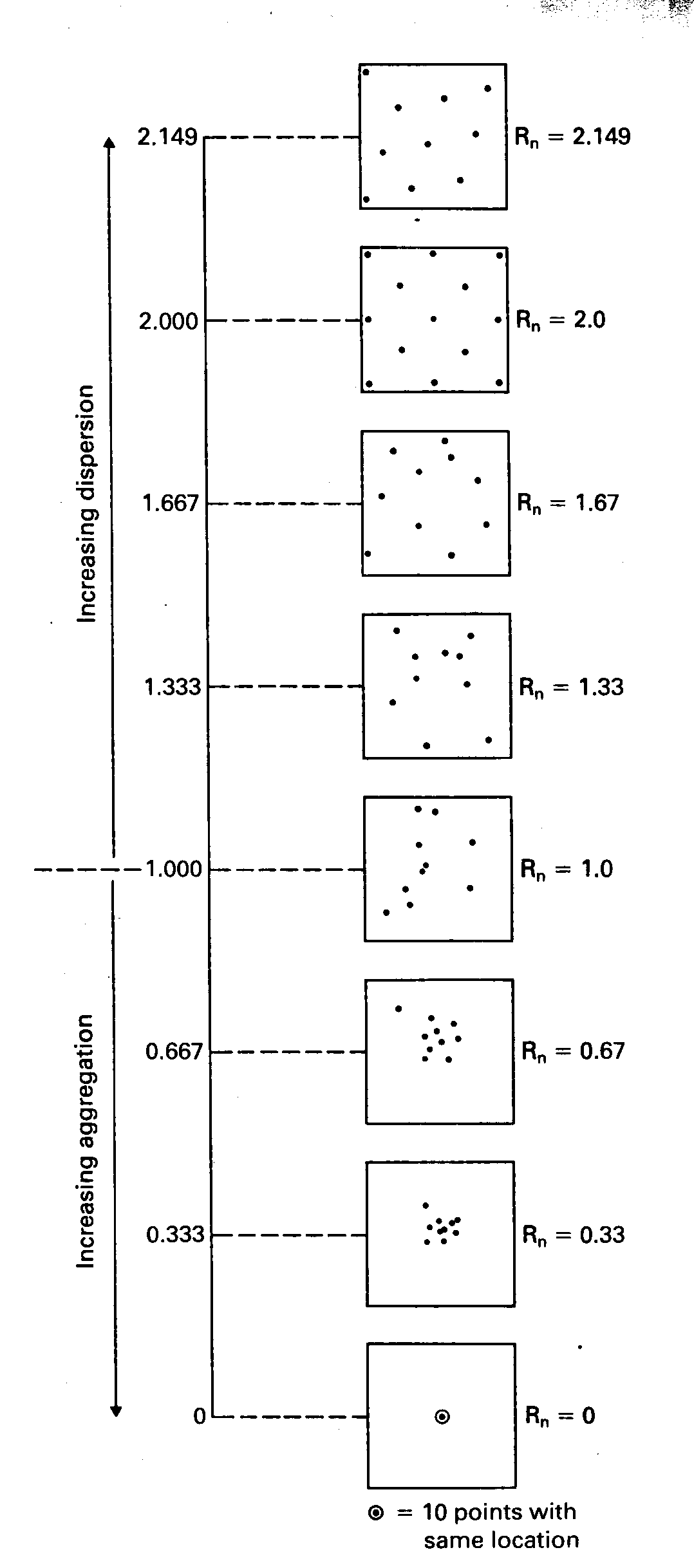
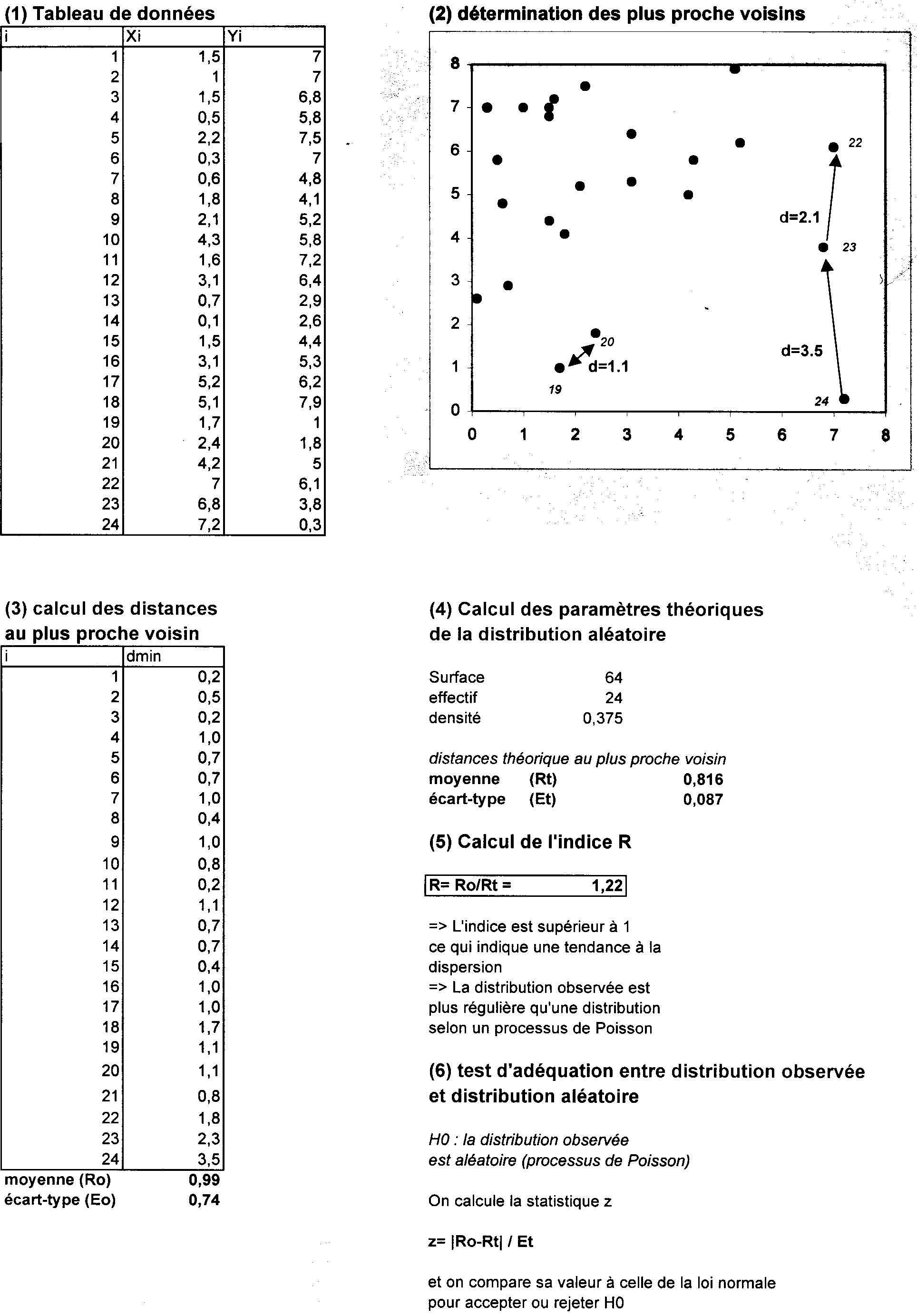 Conclusion : Contrairement
à ce que laisserait penser la première impression visuelle,
la distribution est plutôt dispersée. Mais son caractère
aléatoire ne peut être rejeté.
Conclusion : Contrairement
à ce que laisserait penser la première impression visuelle,
la distribution est plutôt dispersée. Mais son caractère
aléatoire ne peut être rejeté.