|
Analyse spatiale et modélisation des phénomènes géographiques Claude Grasland Université Paris VII / UFR GHSS - Licence de Géographie / Année 2000-2001 / 1er Semestre
|
B.1) Indicateurs globaux
C.1) Analyse des réseaux de transport
Document 1 : VOCABULAIRE DE DESCRIPTION DES GRAPHES
1.1 Nœuds et arêtes / Matrice de connexité
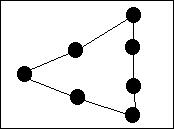
Supposons que quatre équipe A,B,C et D se rencontrent dans une poule de championnat. Au bout de quelques semaines, les rencontres suivantes ont eu lieu : A a rencontré C et D ; B a rencontré D ; C a rencontré A et D ; D a rencontré A, B et C
La liste des rencontres peut être représentée
par un graphe non orienté sous forme de figure ou de
matrice
de connexité symétrique :
| Graphe
des rencontres
|
Matrice
de connexité
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Les équipes A, B, C et D, représentées par des points, sont appelées sommets du graphe, tandis que les rencontres, représentées par des traits, sont appelées arêtes du graphe.
 |
 |
1.3 Graphes complémentaire :
Deux graphes sont complémentaires s'ils n'ont aucune
arête commune et si leur réunion donne un graphe complet.
 |
 |
 |
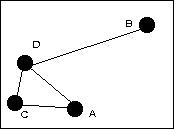 |

Ce graphe est planaire car on peut éviter un croisement des arêtes en changeant leur tracé. |
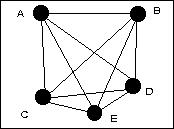
Ce graphe est non-planaire car aucun arrangement ne permet d'éviter le croisement d'au moins deux arêtes. |
 |
|
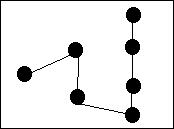
Chemin
 |
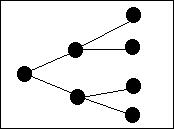
Arbre
 |
Circuit
 |
 |
 |
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.10 Graphes orientés
Dans certains cas, les relations représentées par un graphe ne sont pas symétriques (A peut être en relation avec B sans que B soit en relation avec A) et le graphe doit être orienté. Les sommets sont alors reliés par des flèches et la matrice associée n'est pas nécessairement symétrique.
Dans l'exemple du tournoi de football on peut remplacer
la relation " Les deux équipes A et B se sont rencontrées"
(symétrique) par la relation "L'équipe A s'est déplacé
sur le terrain de l'équipe B pour la rencontrer". La matrice indique
alors les déplacements des équipes et l'on suppose que chaque
équipe rencontre les autres deux fois (match aller et match retour).
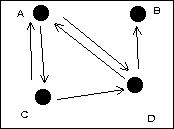 A et C se sont rencontrés à tour de rôle,
tout comme A et D.
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| La somme des lignes indique le nombre de matchs joués à l'extérieur. La somme des colonnes indique le nombre de matchs joués à domicile | |||||
Document 2 : Indicateurs globaux de connexité
Les indicateurs globaux de connexité mesurent le degré de fragmentation d'un graphe en composantes connexes séparées les unes des autres. Soit S le nombre de sommets d'un graphe, C son nombre de composantes connexes et S1..Sk le nombre de sommets de chacune des composantes connexes (S1+S2+…Sk = S), on peut définir deux indices de connexité dont les valeurs sont comprises entre 0 (graphe vide) et 1 (graphe connexe).
Indice de connexité simple : IC1 = (S-C)/(S-1)
Indice de connexité pondéré : IC2 = [ (S1)2
+(S2)2 + … (Sk)2 ] / S2
Exemple d'application :
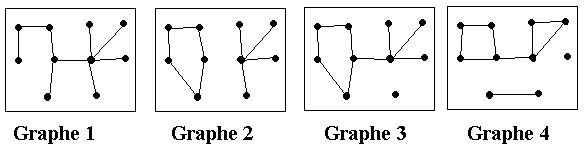
Calcul des indices de connexité :
| Situation | Indice de connexité simple | Indice de connexité pondéré |
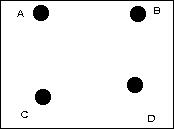
| Graphe 1 | 9/9 = 100% | 100/100 = 100% |
| Graphe 2 | 8/9 = 89 % | (25+25)/100 = 50% |
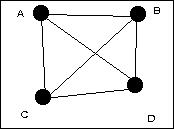
| Graphe 3 | 8/9 = 89 % | (81+1)/100 = 81% |
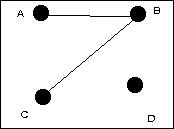
| Graphe 4 | 7/9 = 78% | (49+4+1)/100 = 54 % |
Commentaire :
Document 3 : Indicateurs globaux de connectivité
Les indicateurs globaux de connectivité mesurent la densité et la variété des relations possibles, directes ou indirectes entre les sommets d'un graphe. Ils permettent de préciser les différences entre des graphes connexes (qui ont tous des indices de connexités égaux à 100%). Leur calcul repose sur le nombre de sommets (S), le nombre de liens (L) et le nombre de composantes connexes (C) d'un graphe.
Indicateurs de connectivité basé sur la fréquence des liens
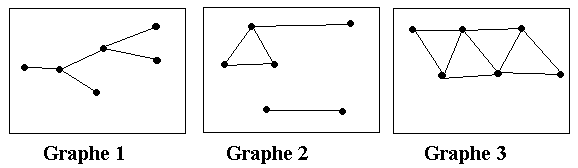
Calcul des indices de connectivité
|
|
|
|
|
|
|
|
|
| Graphe1 |
|
|
|
|
|
|
|
| Graphe2 |
|
|
|
|
|
|
|
| Graphe3 |
|
|
|
|
|
|
|
Document 4 : Indicateurs locaux de position
Les indicateurs locaux de position permettent de mesurer le degré de centralité ou d'accessibilité des différents sommets à l'intérieur d'un graphe. Les avantages relatifs des différents sommets peuvent varier selon le critère retenu.
Exemple d'application
| Sommet | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CD | 1 | 1 | 3 | 4 | 6 | 3 | 3 | 3 | 3 | 3 |
| Dij |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
tot |
|
1
|
-
|
2
|
1
|
2
|
3
|
3
|
4
|
4
|
4
|
3
|
26
|
|
2
|
2
|
-
|
1
|
2
|
3
|
3
|
4
|
4
|
4
|
3
|
26
|
|
3
|
1
|
1
|
-
|
1
|
2
|
2
|
3
|
3
|
3
|
2
|
18
|
|
4
|
2
|
2
|
1
|
-
|
1
|
1
|
2
|
2
|
2
|
1
|
14
|
|
5
|
3
|
3
|
2
|
1
|
-
|
1
|
1
|
1
|
1
|
1
|
14
|
|
6
|
3
|
3
|
2
|
1
|
1
|
-
|
1
|
2
|
2
|
2
|
17
|
|
7
|
4
|
4
|
3
|
2
|
1
|
1
|
-
|
1
|
2
|
2
|
20
|
|
8
|
4
|
4
|
3
|
2
|
1
|
2
|
1
|
-
|
1
|
2
|
20
|
|
9
|
4
|
4
|
3
|
2
|
1
|
2
|
2
|
1
|
-
|
1
|
20
|
|
10
|
3
|
3
|
2
|
1
|
1
|
2
|
2
|
2
|
1
|
-
|
17
|
| CE |
2.9
|
2.9
|
2.0
|
1.6
|
1.6
|
1.9
|
2.2
|
2.2
|
2.2
|
1.9
|
2.1
|
| Sommet | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CM | 4 | 4 | 3 | 2 | 3 | 3 | 4 | 4 | 4 | 3 |
| Sommet | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CI | 0 | 0 | 15 | 18 | 0 | 0 | 0 | 0 | 0 | 0 |
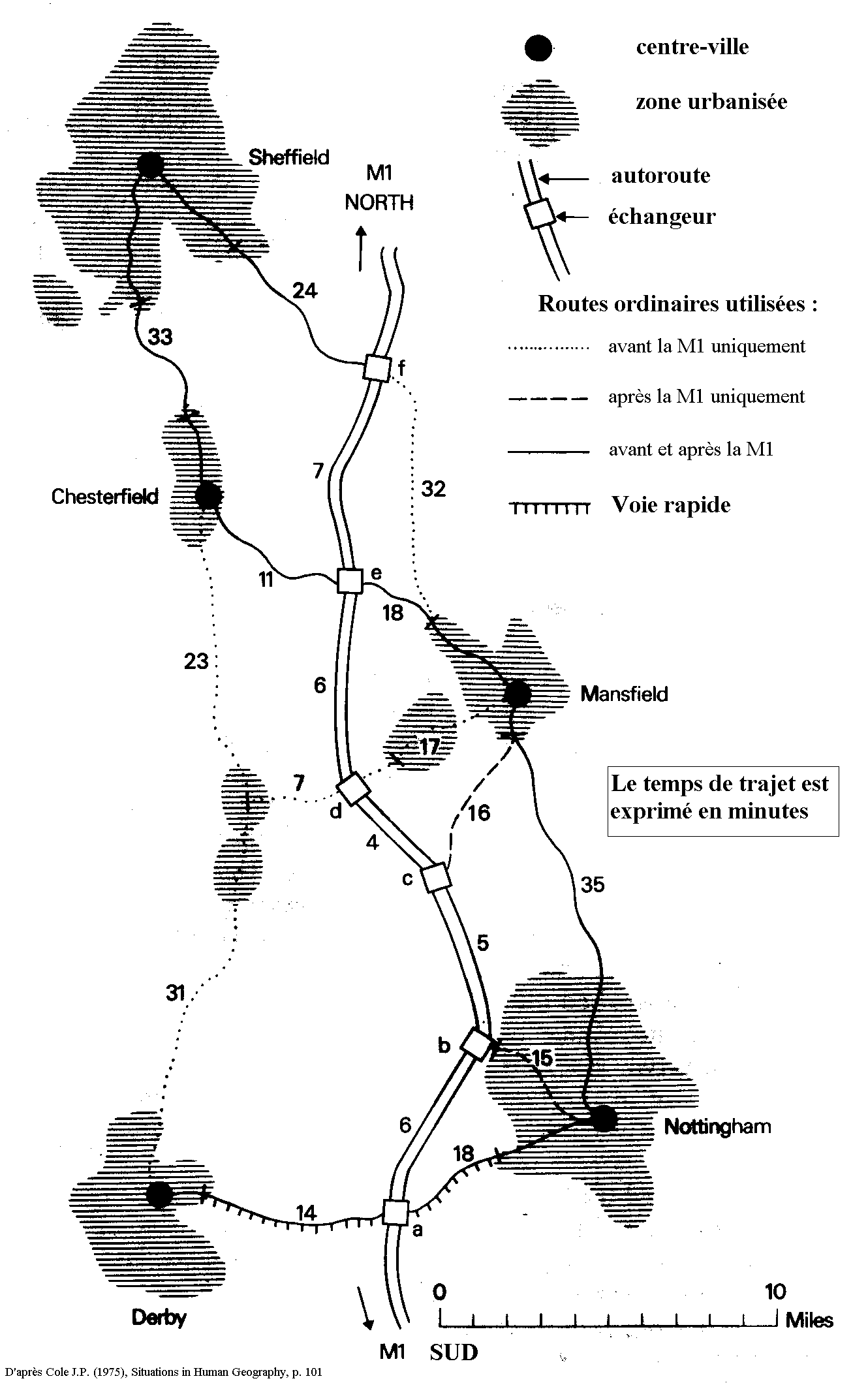
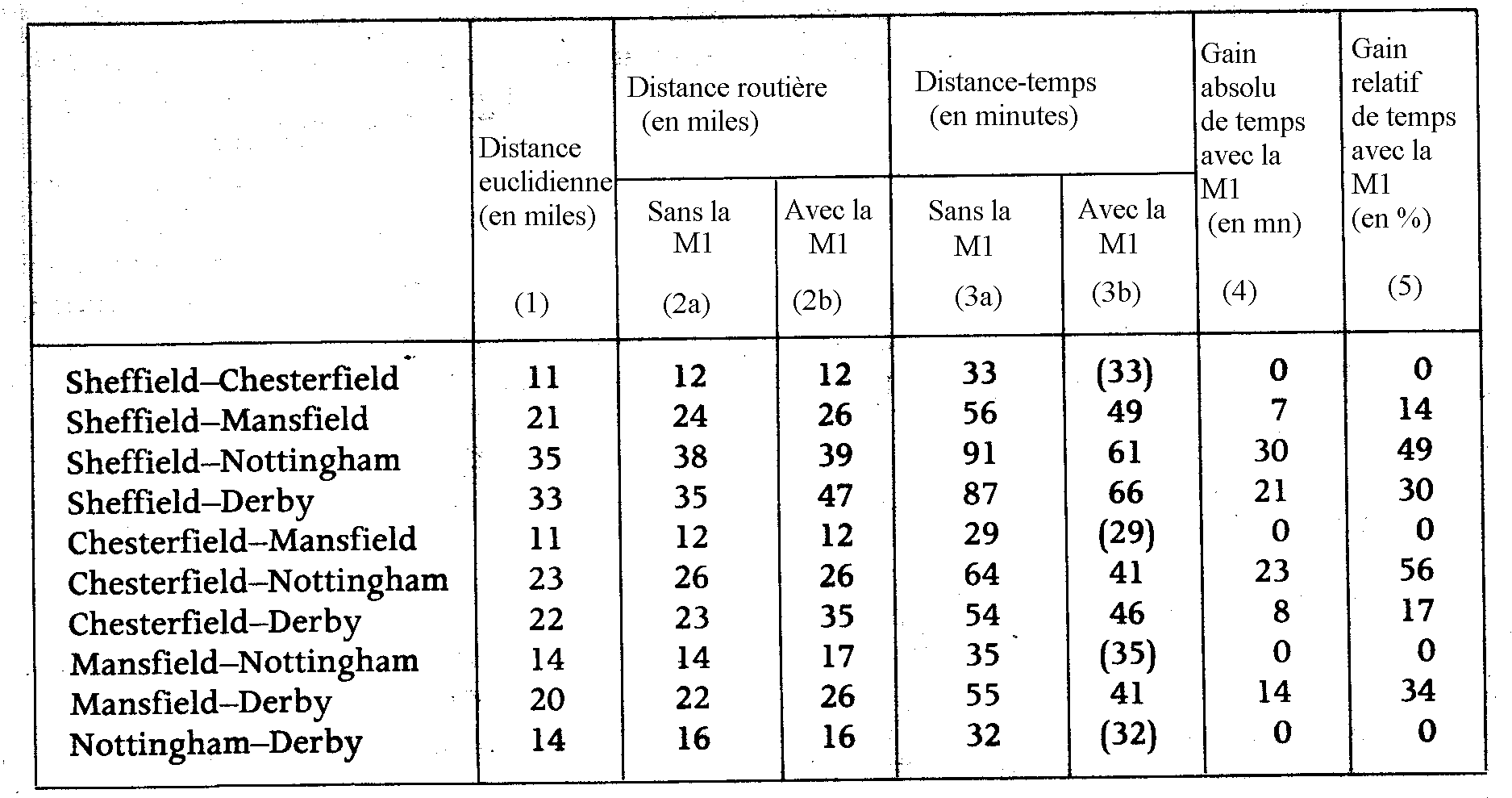
Document 5 : Analyse des réseaux de transport
5.a) Exemple d'une nouvelle autoroute
Source : Cole J.P., 1975, pp. 101-102
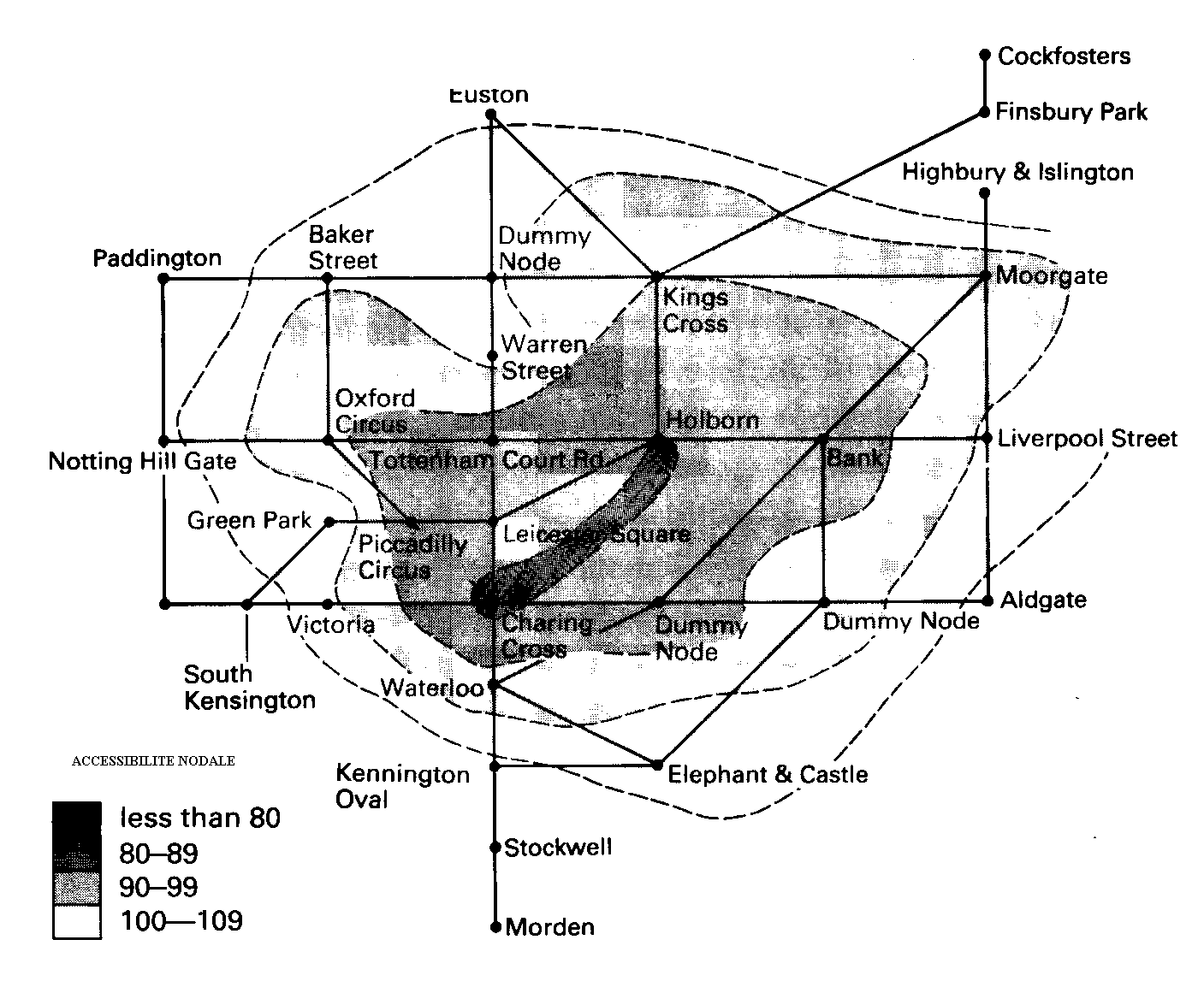
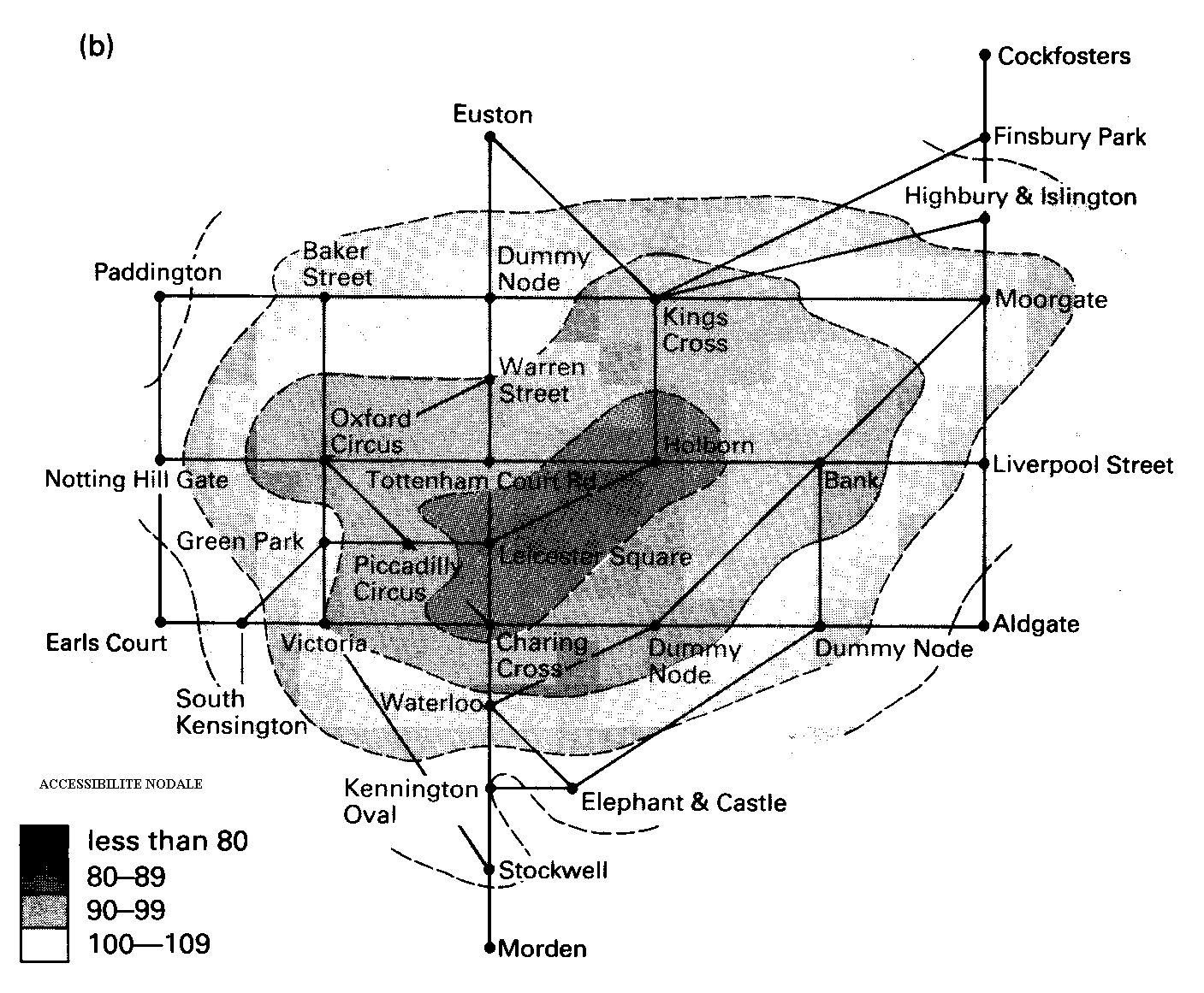
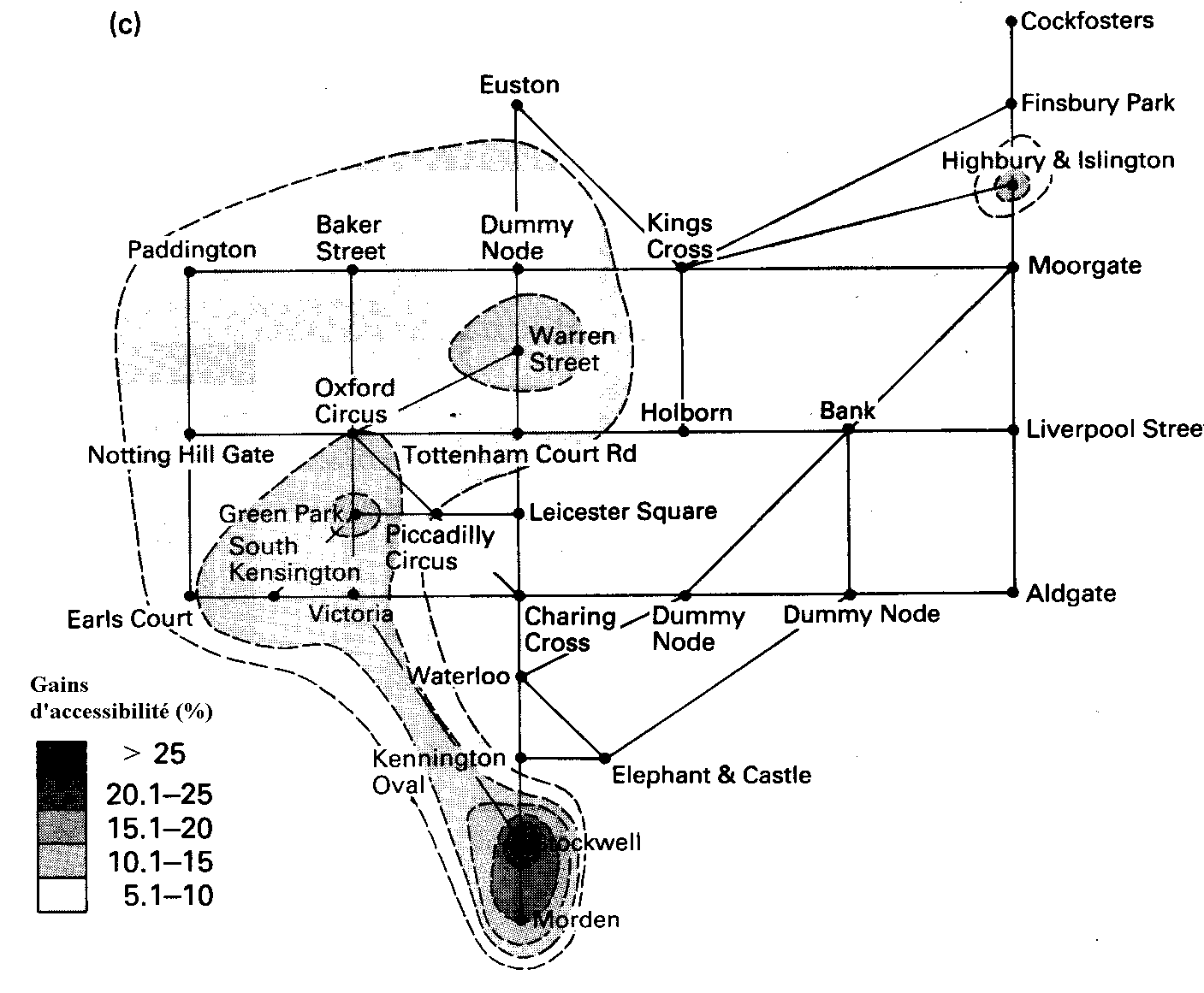
5.b) Exemple d'une nouvelle ligne de métro
Source : Chapman, 1977, pp. 212-214
Document 6 : Analyse des réseaux hydrographiques
6.1) Analyse de la sinuosité des cours d'eau
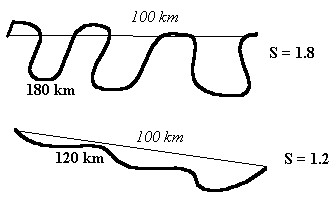
L'indice de sinuosité le plus simple est le rapport entre la longueur du talweg et la distance à vol d'oiseau entre ses extrémités. Toutefois cette méthode est peu fiable (dépend de l'échelle à laquelle on effectue la mesure) et certains auteurs proposent d'utiliser à la place la dimension fractale de la longueur du cours d'eau . Pour plus de détails :
Hauchard E., Delahaye D., Frankhauser P., 1999, "Analyse morphologique de talwegs et comportement scalant", Espace Géographique, 28, 3, pp. 215-224.
6.2) Analyse de la hiérarchie des talwegs à l'aide des lois de Horton
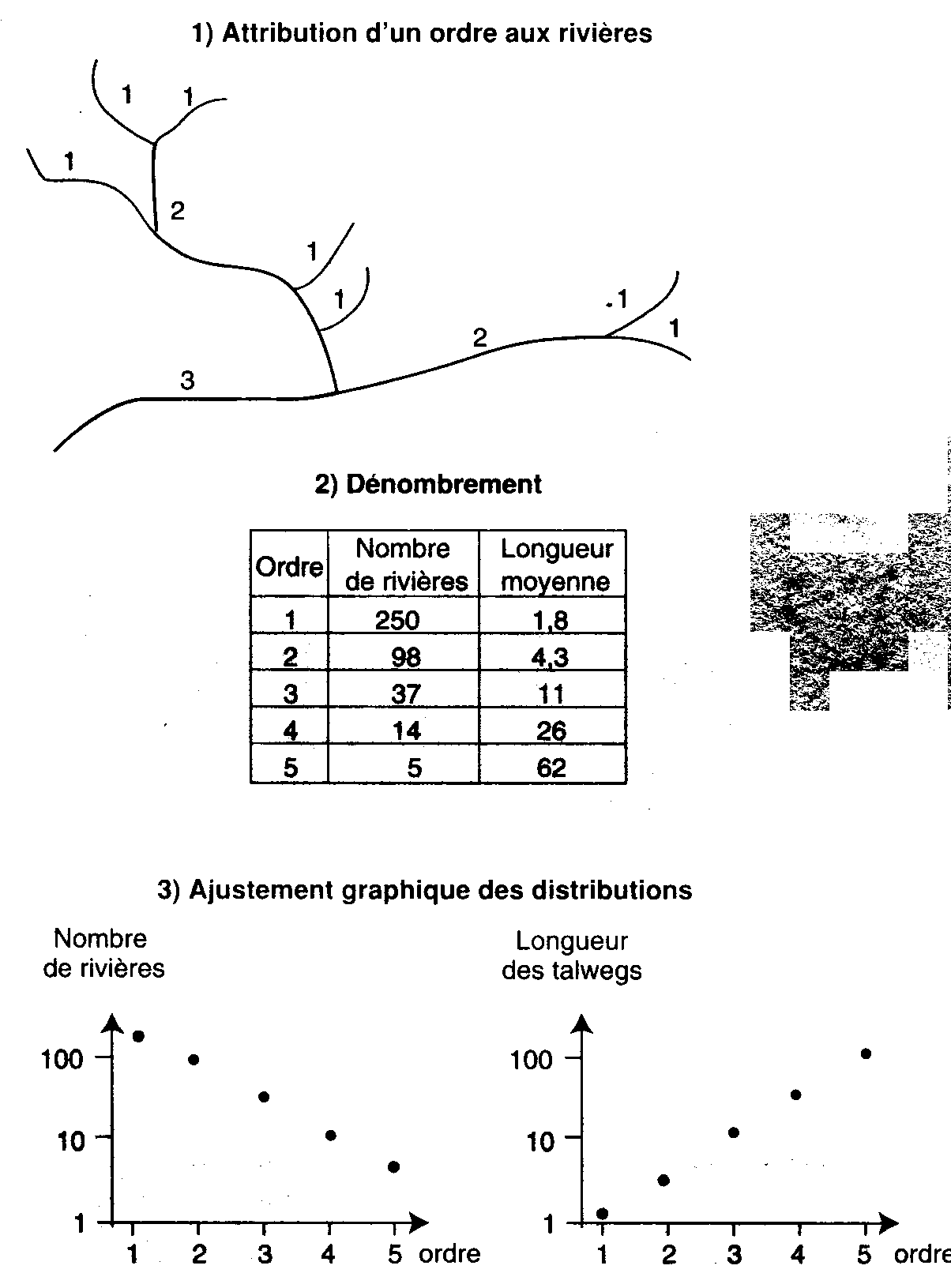
Document 7 : Analyse des réseaux sociaux
Un exemple de réseau social est fourni par le graphe des enseignants de géographie de l'Université Paris 7 pour le critère : "participe au même module d'enseignement".
DEUG 2000-2001
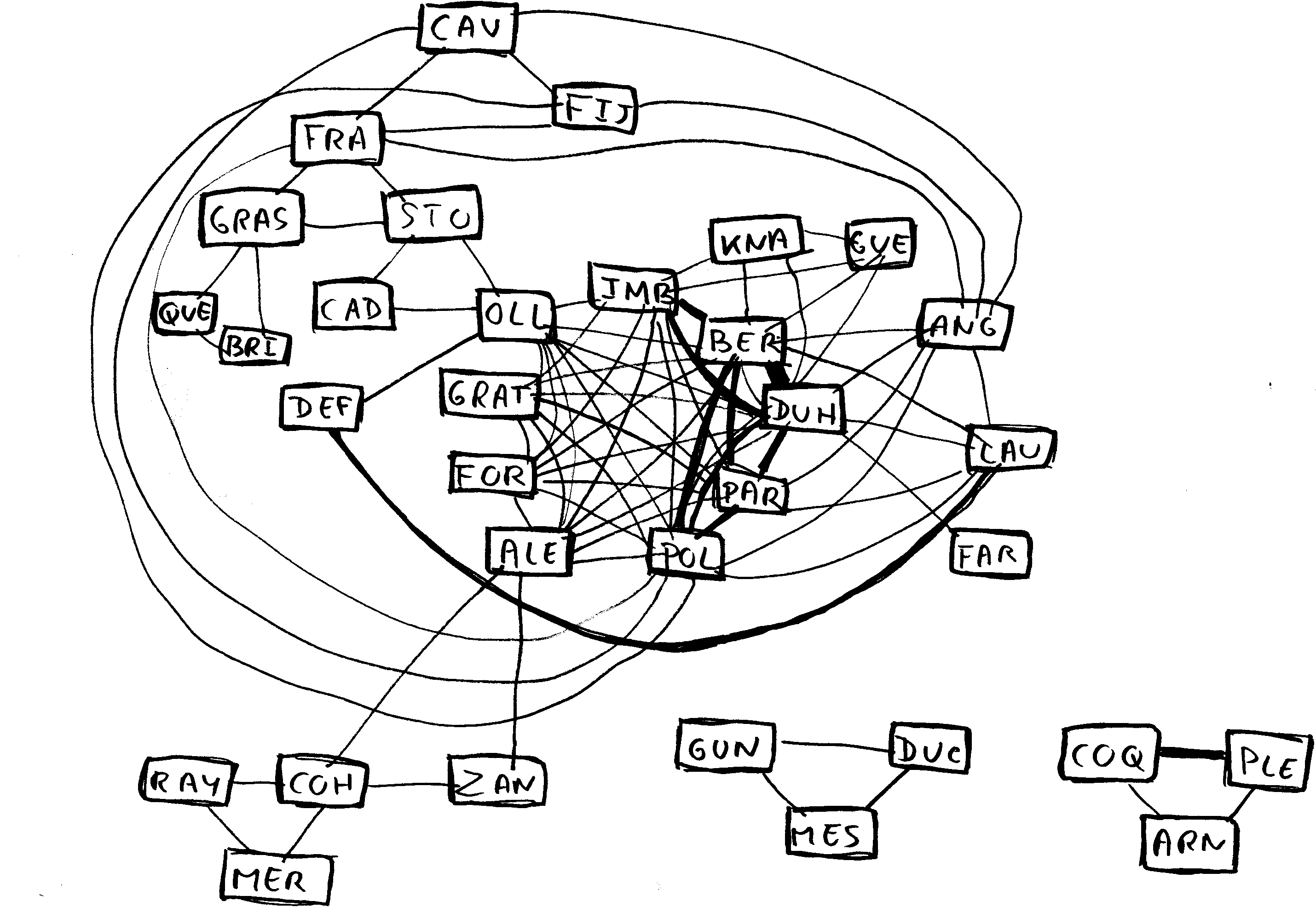
LICENCE 2000-2001
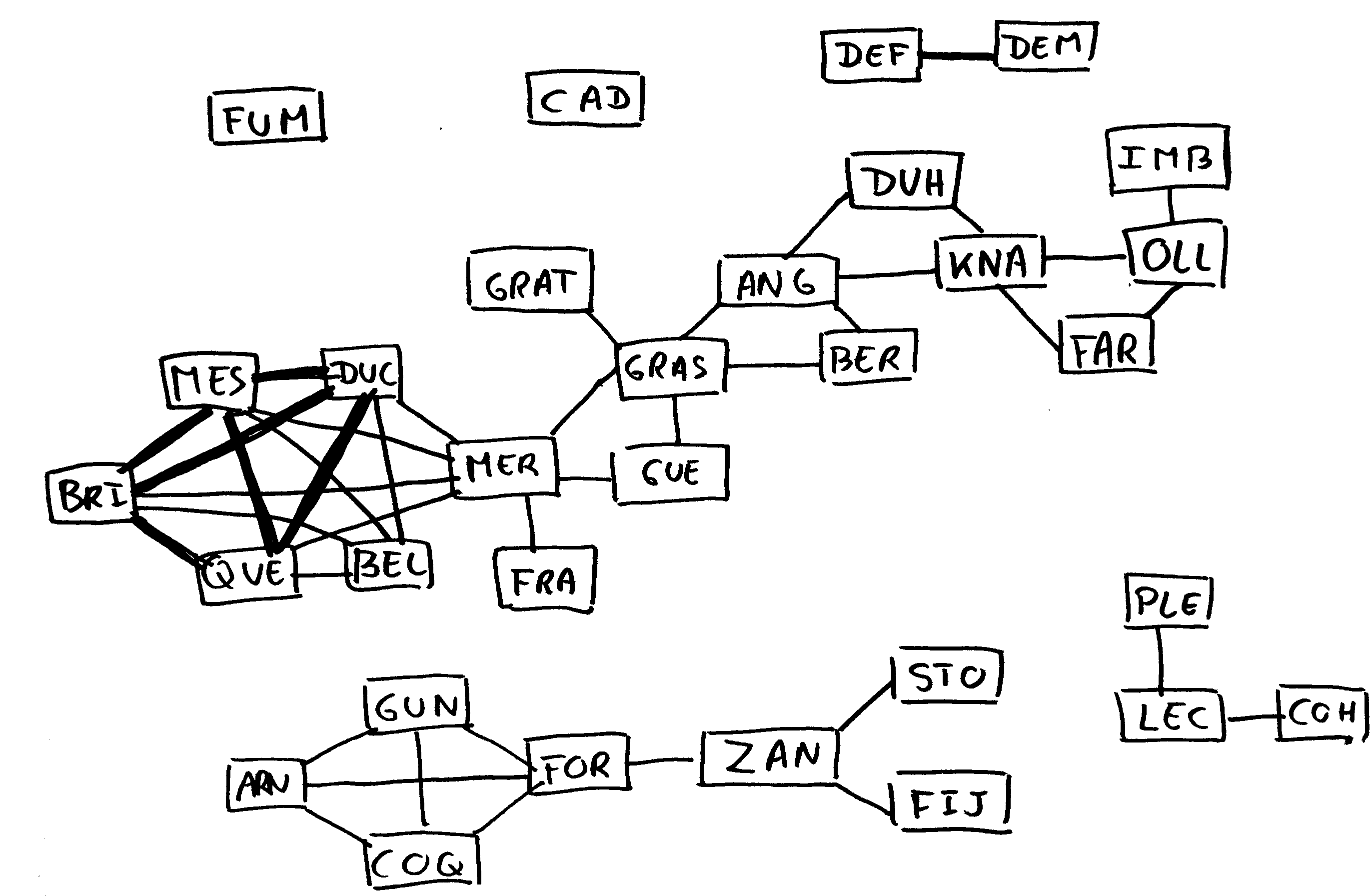
L'analyse de ces graphes permet de repérer les groupes d'enseignants qui travaillent le plus souvent ensemble, les liens indirects qu'ils peuvent nouer, le rôle clé de certains enseignants situés à l'interface entre plusieurs groupes, etc.
On remarquera par exemple, en licence, la position charnière des enseignants de GO303 (Grasland, Mering, Guerois) entre les enseignements de climatologie-télédétection d'une part et les enseignements de géographie régionale ou de géographie humaine d'autre part…