|
Analyse spatiale et modélisation des phénomènes géographiques Claude Grasland
|
A) TYPES DE SURFACES EN GEOGRAPHIE
A.1) Nature de l'information
B) ANALYSE DES PHENOMENES DISTRIBUES SUR UNE GRILLE REGULIERE
B.1 Les opérateurs locaux
C.1) Techniques d'interpolation
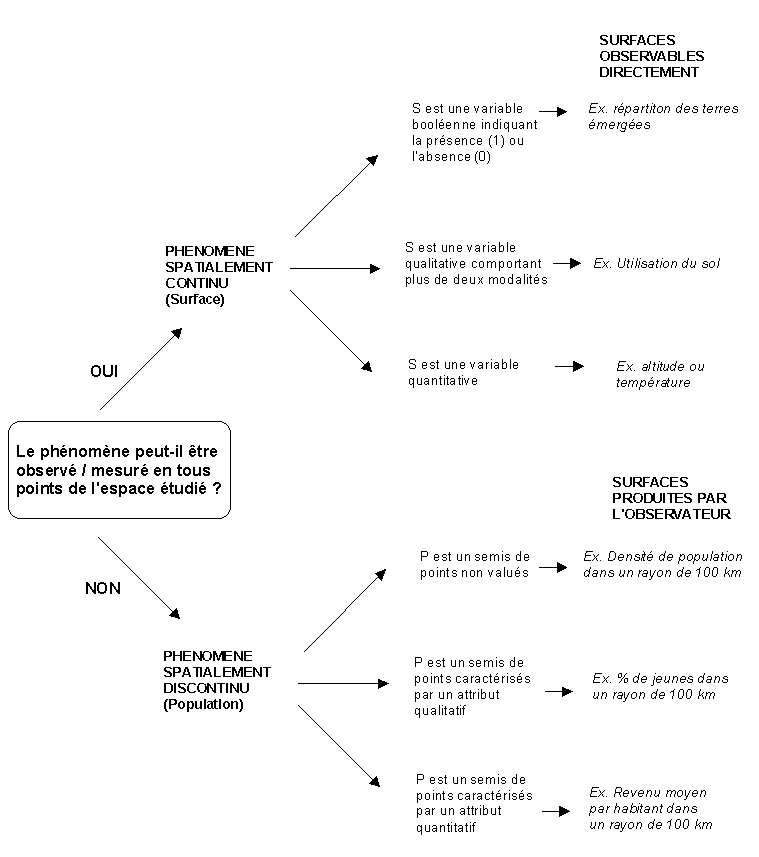
Document 1 : TYPES DE SURFACE ETUDIEES EN GEOGRAPHIE

(1) Certaines surfaces sont le produit d'une observation objective dans la mesure où on peut théoriquement définir leur valeur en tout point de la surface de la Terre par une observation directe du phénomène.
(2) D'autres surfaces sont le produit d'une observation subjective dans la mesure où le phénomène concerné n'est pas défini en tous points de la surface de la Terre, ou peut l'être d'une infinité de manières différentes. Dans ce cas, c'est l'observateur (le sujet) qui définit la nature de ce qui est représenté.
(3) La distinction n'est toutefois pas simple car des phénomènes objectifs peuvent faire l'objet de transformations (altitude moyenne dans un rayon de 50 m) ou d'estimations (carte des températures) lorsque l'information est insuffisante.
Document 2 : TYPE D'INFORMATION
L'analyse d'une surface ne sera pas menée de la même manière selon la manière dont les données ont été recueillies
(a) Grille de collecte & niveau de résolution
Même si un phénomène est objectivement continu, le recueil des informations à son sujet se fait toujours à un certain niveau de résolution qui conduit à éliminer de l'analyse une certaine partie de sa variation spatiale. Ainsi, dans le cas de l'altitude, les modèles numériques de terrain comportent toujours un pas de mesure (5m, 10m, 100 m, 250 m, 1 km, …) qui définit l'espacement des points de collecte des altitudes. L'information est donc toujours plus ou moins dégradée (ou échantillonée) ce qui fait que l'analyse ne pourra repérer que des formes spatiales d'un niveau supérieur au niveau de résolution. Il convient en tous les cas de connaître le mode d'obtention d'une information et la méthode d'agrégation ou de reconstitution qui a été employée s'il ne s'agit pas de données primaires :
Agrégation par calcul des valeurs moyennes (lissage)
 =moyenne=>
=moyenne=> 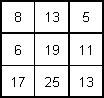 =moyenne=>
=moyenne=> 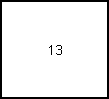
Agrégation par tirage au sort (échantillonage)
 =tir. au
sort=>
=tir. au
sort=>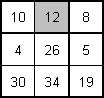 = tir.au sort=>
= tir.au sort=> 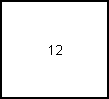
(b) Données primaires et données secondaires
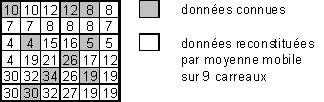
On doit également toujours se demander si l'information dont on dispose a fait l'objet d'une collecte directe (information primaire) ou bien si elle a été reconstituée à partir d'un échantillon de valeurs connues uniquement en certains points (information secondaire). Le traitement de données secondaires est toujours délicat car les résultats que l'on va obtenir peuvent être influencés voire faussés par la méthode de reconstitution qui a été utilisée.
Interpolation de données manquantes par moyenne mobile
 = interpolation
=>
= interpolation
=> 
Document n°3 : OPERATEURS LOCAUX SUR GRILLE REGULIERE
On considère un espace rectangulaire E (Xmin, Ymin, Xmax,Ymax) pour lequel on dispose d'une grille régulière de N points (Xi,Yi) affectés d'une valeur Zij.
(a) Voisinages dans une grille
Un voisinage est une fonction de pondération W qui associe à
tout point (i,j) une valeur de relation avec ses voisins (et avec lui-même)
comprise entre 0 et 1 et telle que la somme des valeurs de W soit égale
à 1. Le voisinage peut se limiter aux cellules contiguës ou
inclure des cellules plus éloignées.
| Coordonnées (i,j) | Valeurs de Z(i,j) | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Voisinage 1 | Voisinage 2 | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Les opérateurs locaux sont des fonctions f(Z,W) qui à tout point (i,j) de la grille associent une nouvelle valeur qui dépend des valeurs de la variable Z dans son voisinage W. Ils peuvent mesurer la valeur moyenne, la valeur maximale, la valeur minimale, la variance locale, le gradient local, etc. On se limitera ici à 2 exemples : la moyenne locale et le gradient local.
Moyenne locale
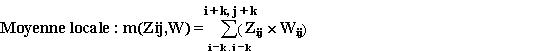
Exemple : pour le voisinage 1, la moyenne locale est
(80+90+100+110+130)/5 = 510/5 = 102 m
Pour le voisinage 2, la moyenne locale est [ 100/4
+(80+90+110+130)/8 + (110+90+120+150)/16] = 105.7 m
Gradient local :

Exemple : Si la grille a un pas de 250 m, on trouve
:
GradX = 50/500 = 0.1 = 10% GradY=20/500 = 0.04 = 4%
L'intensité du gradient est égale à
= 10.8%
La direction du gradient est Arctan(0.04/0.10) = 21°
ou -158°. Il y a toujours deux solutions de direction opposée
et il faut regarder les signes de gradX et gradY pour trouver la bonne
solution. Ici, la réponse est -158° ce qui signifie une
décroissance ENE/WSW
Document n°4 : INFLUENCE DU NIVEAU D'ANALYSE SUR LE CALCUL DES GRADIENTS
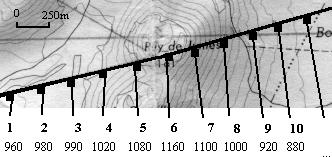
Sur une carte au 1/50 000e de Clermont-Ferrand, on a réalisé une coupe topographique de direction Ouest-Est, à la hauteur de Chateaugay. Sur cette coupe de 25 km de longueur, on a relevé un échantillon de 100 points d'altitude, régulièrement espacés tous les 250 mètres.
(a) Altitude moyenne et gradients pour un pas de 250 m
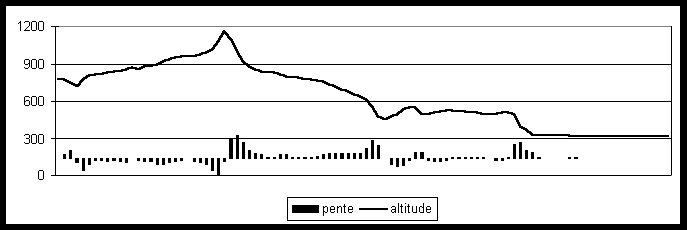
(b) Altitude moyenne et gradients dans un voisinage de 2 km
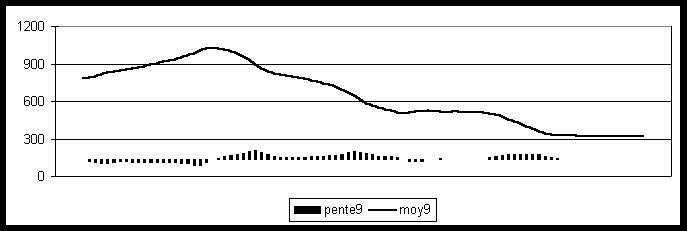
(c) Altitude moyenne et gradients dans un voisinage de 4 km
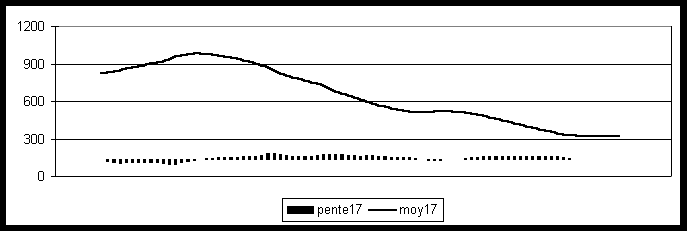
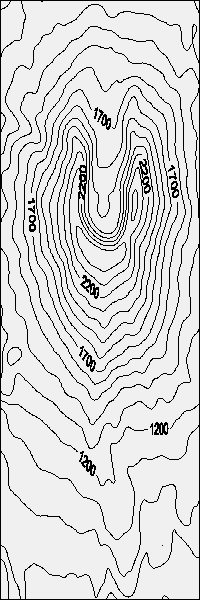
DOCUMENT n°6 : VISUALISATION D'UN RELIEF
Exemple du Mount St Helens (Etats-Unis)
Altitude (non lissée)
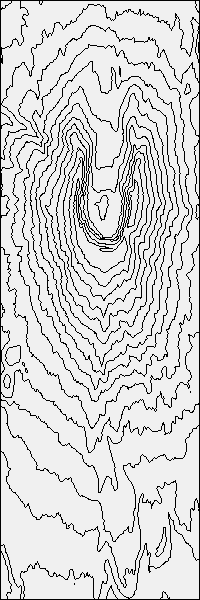 |
Altitude (lissée)
 |
Pentes (non lissées)
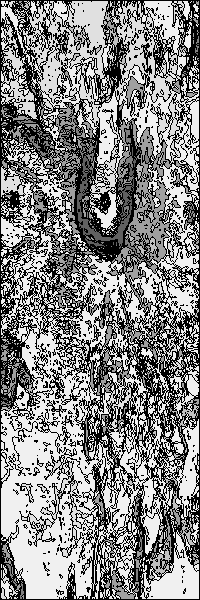 |
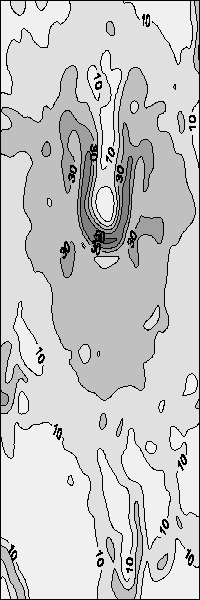
Pentes (lissées)
 |
Vue 3D depuis le sud-ouest
 |
Vue 3D depuis le nord-est
 |
Document n°7 : INTERPOLATION ET AJUSTEMENT D'UNE SURFACE CONNUE EN CERTAINS POINTS SEULEMENT
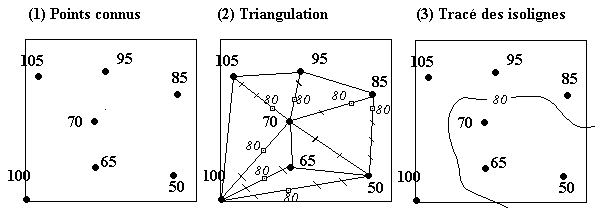
(b) Surfaces de tendances
Une autre solution consiste à chercher l'équation d'une
fonction Z=f(X,Y) qui s'ajuste le mieux aux informations connues, puis
à extrapoler les résultats de cette fonction à l'ensemble
de l'espace étudié. On utilise souvent des fonctions polynomiales
de degrés plus ou moins élevés pour procéder
à de tels ajustements :
Les surfaces de tendance d'ordre 1 et 2 sont les plus utilisées car leurs coefficients ne sont pas trop nombreux et peuvent faire l'objet d'interprétations. Dans le cas des plans de tendance (surfaces d'ordre 1), les coefficients a et b permettent de calculer la valeur moyenne du gradient principal et sa direction :
Intensité du gradient
= racine (a2+b2)
Direction du gradient
= ArcTangente (b/a)
On peut également calculer et cartographier les résidus d'une surface de tendance, afin de repérer les exceptions positives ou négatives qui signalent des spécificités locales.
Document n°8: APPLICATION DES SURFACES DE TENDANCE
Le PNB/hab. des régions de l'Union Européenne en 1996
(a) tableau de données (extrait)
| CODE |
|
|
|
|
|
131
|
|
|
|
|
|
155
|
|
|
|
|
|
92
|
|
|
|
|
|
105
|
|
|
|
|
|
74
|
|
|
|
|
|
…
|
|
|
|
|
(b) Ajustement à une surface de tendance d'ordre
1
PNB = 0.88 X + 3.90 Y + 7580 (r2 = 19.5%)

Commentaire :
On déduit de l'équation que le gradient principal de
richesse par habitant à l'intérieur de l'Union Européenne
est de direction NNE-SSW. Le calcul du gradient de richesse indique une
diminution moyenne de 4 euros/habitants par kilomètre quand on va
du NNE vers le SSW. Toutefois, la qualité de l'ajustement obtenue
est très médiocre (r2=19.5%) et le modèle
proposé ne peut être retenu pour décrire les variations
de richesse à l'intérieur de l'Union Européenne.
(c) Ajustement à une surface de tendance d'ordre
2
PNB = -20.1 X - 8.28 Y + 0.032 XY + 0.0054 X2
-0.0013 Y2 - 0.0000088 X2Y- 0.000004 XY2
+ 0.0000000014 X2Y2 + 14857 (r2 = 51.1%)
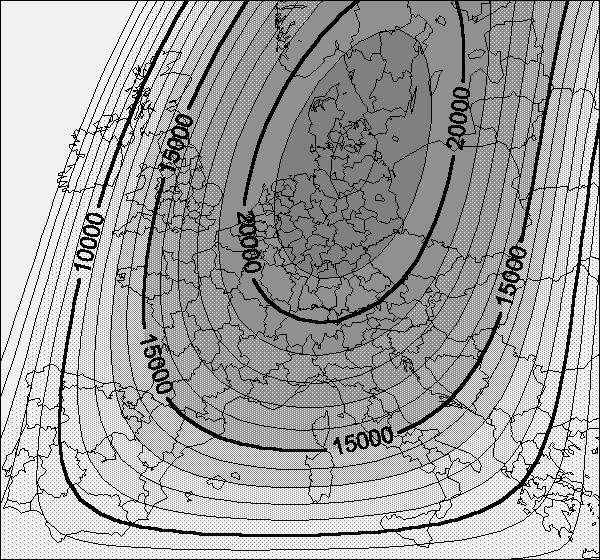
Commentaire :
L'ajustement à une surface quadratique donne un ajustement nettement
meilleur (r2=50%) que dans le cas précédent. En
effet, les inégalités de revenus en Europe correspondent
davantage à une opposition centre-périphérie qu'à
un simple gradient Nord-Sud. On pourrait poursuivre l'analyse en examinant
les résidus des régions par rapport à cette surface
de tendance d'ordre 2.