A) LA CONSTRUCTION D'UNE MATRICE DE SIMILARITE

A.1) Problèmes généraux

• Subjectivité de la notion de ressemblance
• Variété des critères possibles
• Effets contextuels

• Cas d'un indicateur unique
• Cas d'un ensemble d'indicateurs
• Cas d'une série temporelle

B.1 Approche statistique : l'analyse de la variance

• Variations intra-régionale et inter-régionales
• Test de Fischer

• Construction d'une matrice d'appartenance commune
• Mesure de l'autocorrélation territoriale

C.1) Approche statistique : les indices de Geary & Moran

• Indice de Geary
• Indice de Moran

• Construction d'une matrice de contiguïté
• Mesure de l'autocorrélation spatiale

• La fécondité des régions européennes en 1988

Document 1 : La construction d'une matrice de similarité

Exemple 1 : Mesure des proximités linguistiques entre les pays d'Europe

(a) Deux pays ont-ils la même langue officielle ?
 

Attributs			Similarité
Pays (i)	Langue officielle (Xi)		Sij	France	Allemagne	Autriche
France	Français		France	1	0	0
Allemagne	Allemand		Allemagne	0	1	1
Autriche	Allemand		Autriche	0	1	1

(b) Quelle est la probabilité que deux habitants de chaque pays parlent la même langue ?
 

Attributs
Pays(i)	Langues parlées (%)					Similarité
.	FR	AL	IT	NE		Sij	Fra	Bel	Sui	Ita
France	100	0	0	0		Fra	100	40	20	0
Belgique	40	2	0	57		Bel	40	100	9.5	0
Suisse	20	75	5	0		Sui	20	9.5	100	5
Italie	0	0	100	0		Ita	0	0	5	100

Exemple 2 : Mesure des dissimilarités pour un attribut quantitatif
 

			Dissimilarité 1 : abs(Xi-Xj)
			Sij	Aut	Rou	All
			Aut	0	15.3	17.4
			Rou	15.3	0	32.7
			All	17.4	32.7	0
Attributs
Pays	Tx mort. Inf (88)		Dissimilarité 2 : (Xi-Xj)2
(i)	(Xi)		Sij	Aut	Rou	All
Autriche	10.3		Aut	0	234	303
Roumanie	25.6		Rou	234	0	1069
Albanie	43.0		All	303	1069	0
			Dissimilarité 3 : abs(Xi-Xj) / min(Xi,Xj)
			Sij	Aut	Rou	Alb
			Aut	0%	149%	68%
			Rou	149%	0%	317%
			Alb	68%	317%	0%

Exemple 3 : Mesure des dissimilarités pour plusieurs attribut quantitatif

Variables standardisées Différence moyenne (en écart-type)
 

PAYS	PNB	TMI	ESP	URB	FEC			DS	ALB	AUT	BEL	BUL	ROU	HON
ALB	-0.9	2.0	-0.6	-1.4	2.0			ALB	0.0	2.3	2.6	1.4	0.9	1.3
AUT	1.5	-0.9	1.3	-0.2	-1.0			AUT	2.3	0.0	0.5	1.1	1.5	1.2
BEL	1.3	-0.9	1.3	1.9	-0.9			BEL	2.6	0.5	0.0	1.2	1.9	1.5
BUL	-0.6	-0.5	-0.1	0.3	-0.1			BUL	1.4	1.1	1.2	0.0	0.7	0.4
ROU	-0.8	0.5	-1.0	-0.6	0.4			ROU	0.9	1.5	1.9	0.7	0.0	0.4
HON	-0.6	-0.1	-1.0	-0.1	-0.4			HON	1.3	1.2	1.5	0.4	0.4	0.0

 

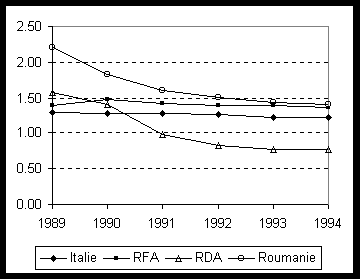
Exemple 4 : Mesure des dissimilarités entre séries temporelles

Evolutions récentes de la fécondité en Europe Centrale

Dissimilarités moyennes de niveau
 

Année	1989	1990	1991	1992	1993	1994			Dsij	Ita	RFA	RDA	Rou
Italie	1.29	1.27	1.27	1.26	1.21	1.22			Ita	0.00	0.15	0.34	0.41
RFA	1.39	1.48	1.42	1.40	1.39	1.35			RFA	0.15	0.00	0.41	0.26
RDA	1.58	1.41	0.98	0.83	0.77	0.77			RDA	0.34	0.41	0.00	0.61
Roumanie	2.20	1.83	1.60	1.51	1.44	1.41			Rou	0.41	0.26	0.61	0.00

Dissimilarités moyennes d'évolution
 

Années	89-90	90-91	91-92	92-93	93-94			Dsij	Ita	RFA	RDA	Rou
Italie	-2%	0%	-1%	-4%	1%			Ita	0%	3%	10%	6%
RFA	6%	-4%	-1%	-1%	-3%			RFA	3%	0%	11%	7%
RDA	-11%	-30%	-15%	-7%	0%			RDA	10%	11%	0%	6%
Roumanie	-17%	-13%	-6%	-5%	-2%			Rou	6%	7%	6%	0%

Convergence des niveaux
 

Dif89	Ita	RFA	RDA	Rou
Ita	0.00	0.10	0.29	0.91
RFA	0.10	0.00	0.19	0.81			(Dif89 - Dif94)/(Dif89)
RDA	0.29	0.19	0.00	0.62			Dsij	Ita	RFA	RDA	Rou
Rou	0.91	0.81	0.62	0.00			Ita	0%	-30%	-55%	79%
							RFA	-30%	0%	-205%	93%
Dif94	Ita	RFA	RDA	Rou			RDA	-55%	-205%	0%	-3%
Ita	0.00	0.13	0.45	0.19			Rou	79%	93%	-3%	0%
RFA	0.13	0.00	0.58	0.06
RDA	0.45	0.58	0.00	0.64
Rou	0.19	0.06	0.64	0.00

 

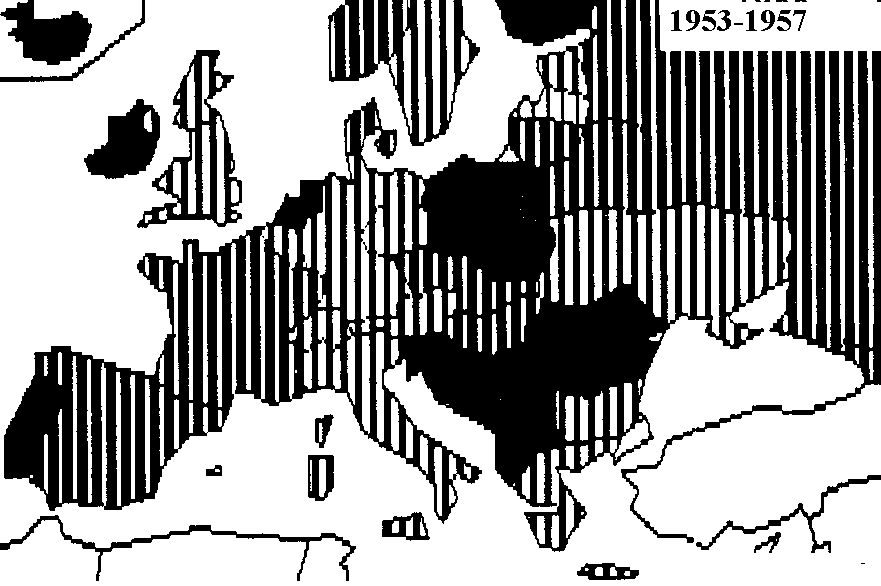
Document 2 : Analyse des similarité des évolutions de fécondité des pays d'Europe et de 8 républiques soviétiques (1952-1982)
Source : Grasland C., 1990, Systèmes démographiques et systèmes supranationaux : la fécondité européenne de 1952 à 1982, European Journal of Population, 6, pp. 163-191

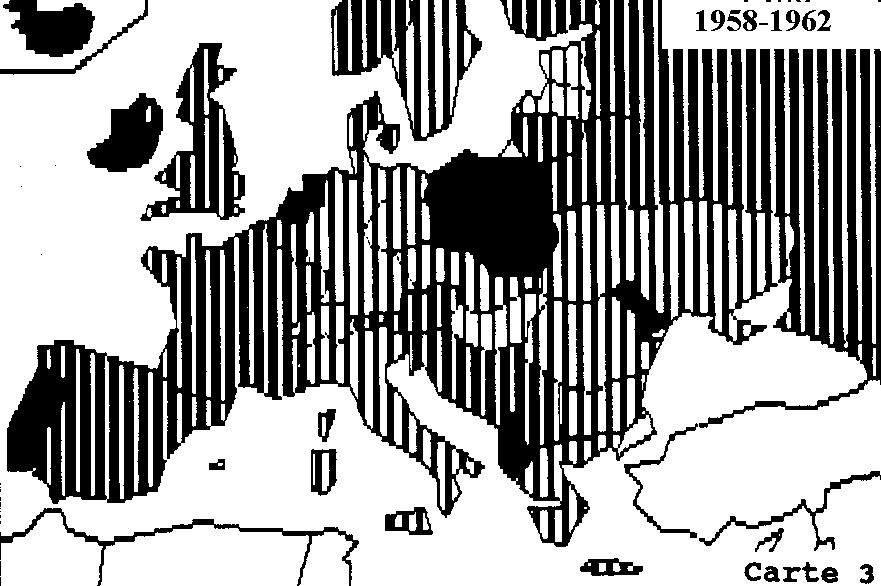
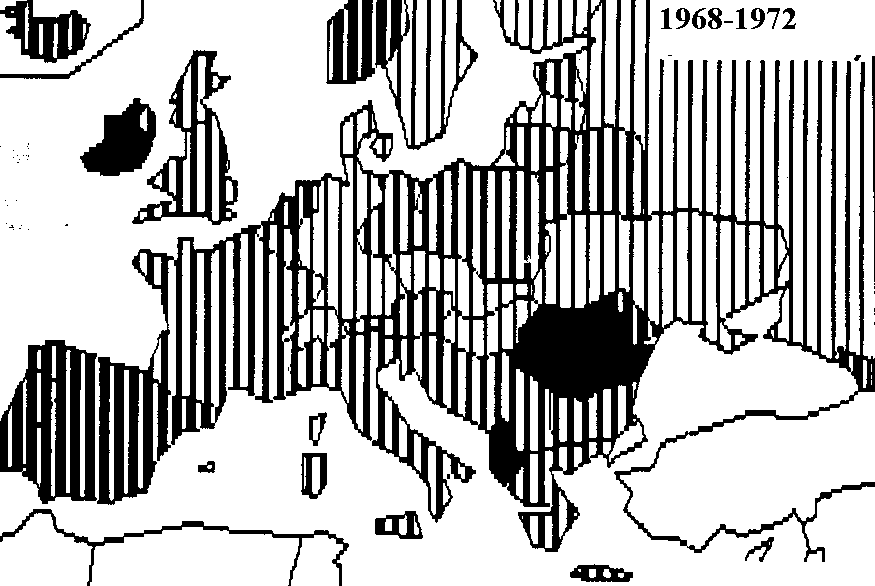
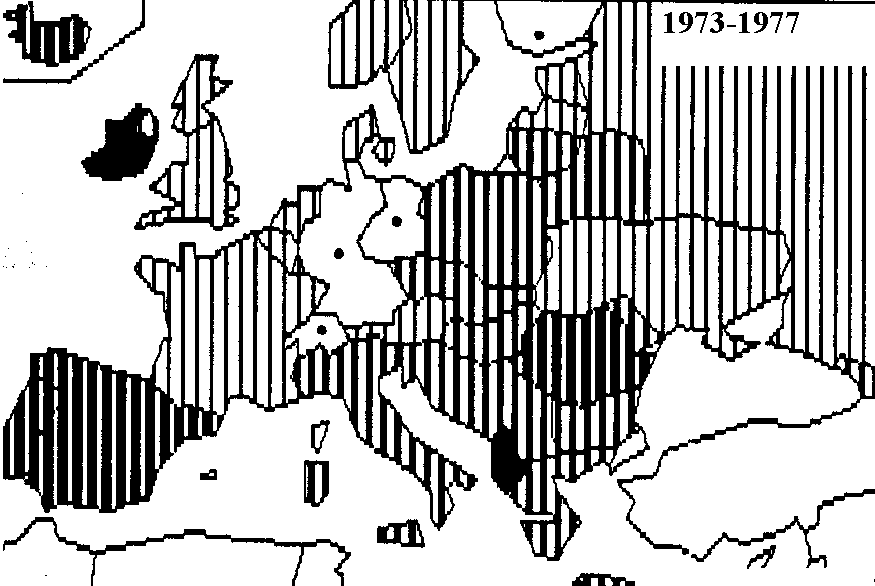
Evolution de la fécondité des pays d'Europe et de 8 républiques socialistes soviétiques

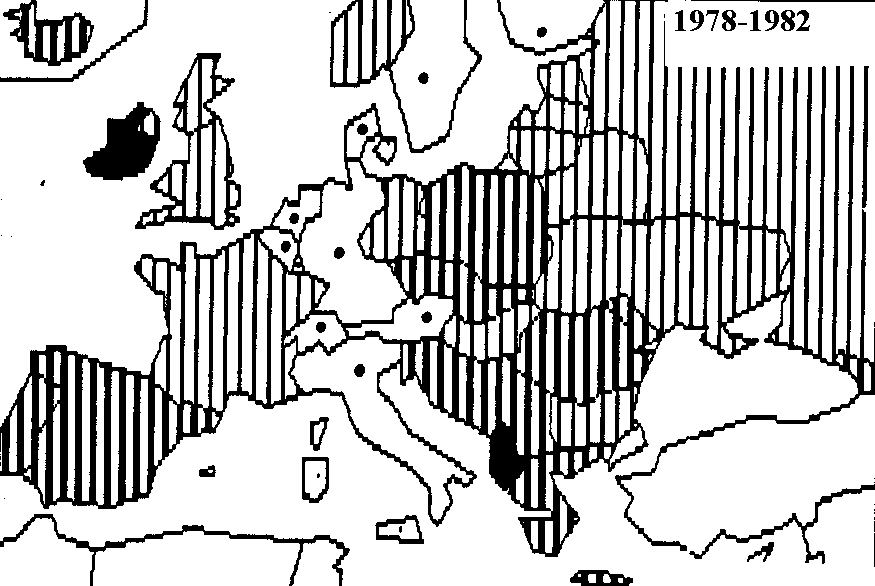Corrélation entre les évolutions de fécondité (1952-1982)

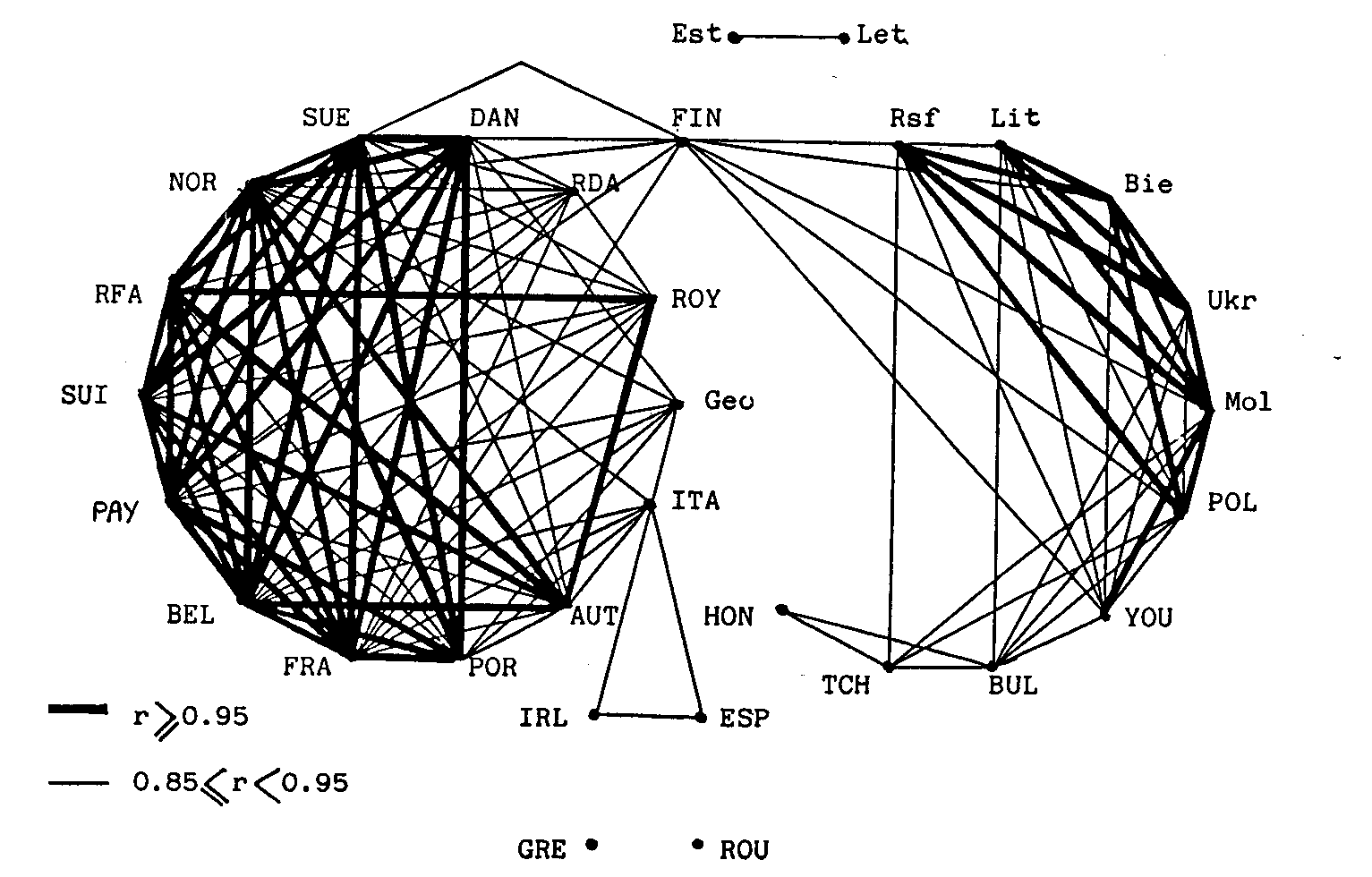Identification de deux modèles d'évolution de la fécondité en Europe
 

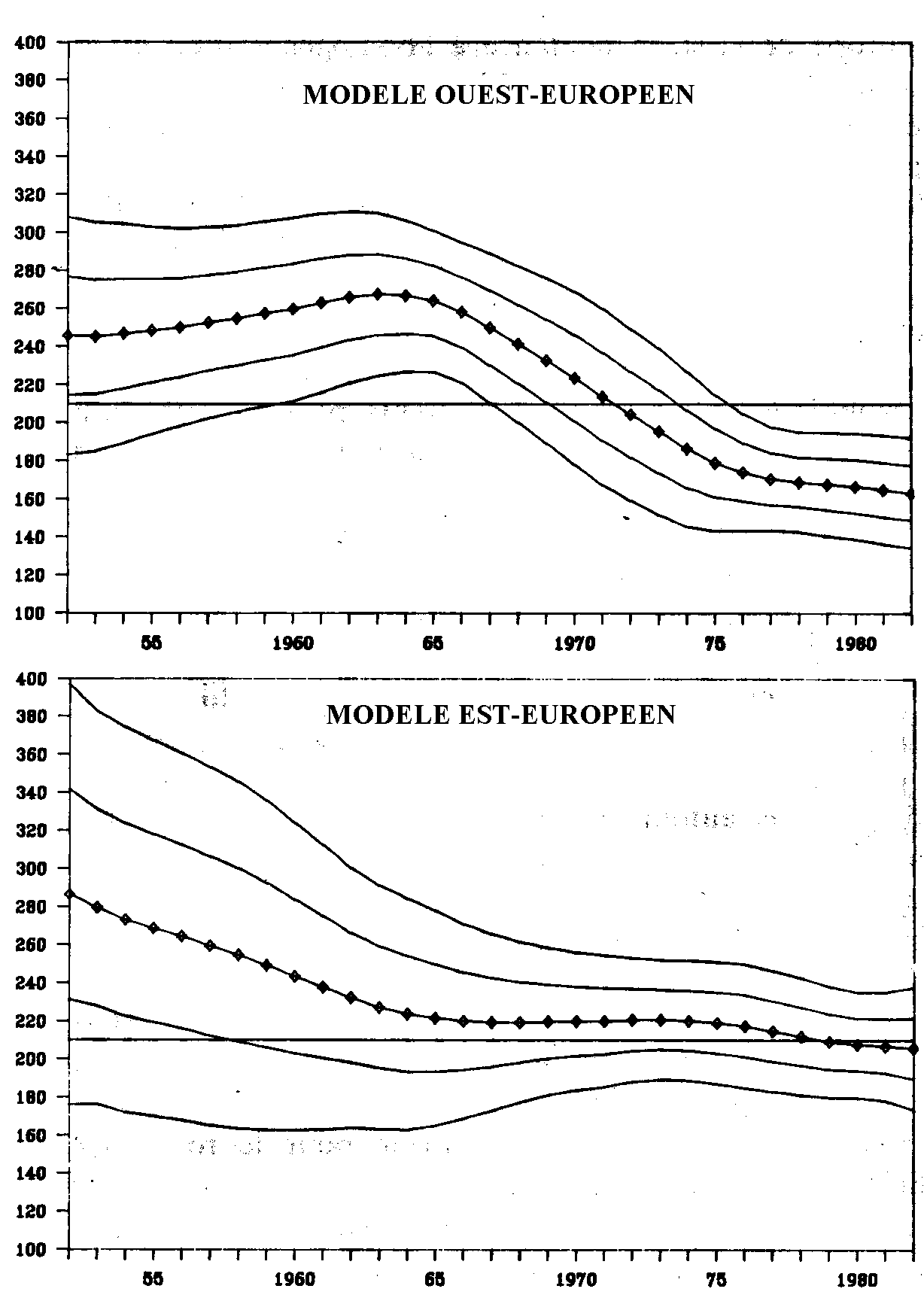Document 3 : Analyse des effets d'appartenance territoriale

(a) Définition des effets d'appartenance territoriale

On considère un ensemble de n lieux 1..i...N divisé en k régions R1..Rj..Rk et caractérisés par un attribut quantitatif X (X1..Xi…Xn). On souhaite déterminer s'il existe une relation entre l'appartenance des lieux aux différentes régions et la valeur de leur attribut X.

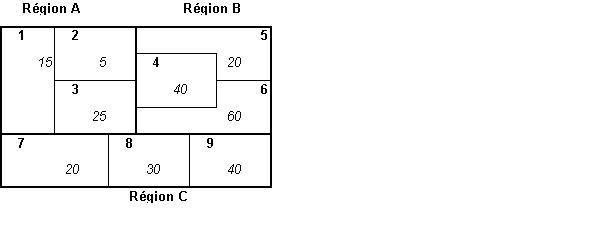
Les chiffres en gras correspondent au code des unités et les chiffres en italiques à la valeur de l'attribut X.

(b) Une solution statistique particulière : l'analyse de la variance

On peut évaluer statistiquement l'importance de l'effet d'appartenance en décomposant la variation totale de l'indicateur X en deux composantes : la variation intra-régionale et la variation inter-régionale.
 

Unités	Régions	Valeur de l'indicateur			Variance de l'indicateur
i	j	Xi	Xj	Xtot	(Xi-Xtot)2	(Xi-Xj)2	(Xj-Xtot)2
1	A	15	15	25	100	0	100
2	A	5	15	25	400	100	100
3	A	25	15	25	0	100	100
4	B	40	40	25	225	0	225
5	B	20	40	25	25	400	225
6	B	60	40	25	1225	400	225
7	C	10	20	25	225	100	25
8	C	20	20	25	25	0	25
9	C	30	20	25	25	100	25
				Total	2250	1200	1050

Dans l'exemple ci-dessus la variation totale (2250) correspond à 53% de variations intra-régionale (1200) et 47% de variations inter-régionales (1050). D'un point de vue statistique, on peut dire que l'appartenance régionale "explique" 47% des différences de niveau entre les unités spatiales pour le critère X.

N.B. Un test statistique (test F de Fischer-Snedecor) permet de vérifier si cet effet d'appartenance régionale est significatif ou non. Si on note n le nombre d'unités et k le nombre de régions, on trouve :

F_obs = [(variation inter-régionale) / (k-1) ] / [(variation inter-régionale) / (n-k) ]= 2.625

F_théorique = F(k-1,n-k, a ) lu dans la table de Fischer-Snedecor pour un risque d'erreur a

• Si on se fixe un risque d'erreur de 5%, on trouve F_théorique =F(2,6,0.05) = 5.14 donc on ne peut rejeter H0 et on conclue que l'effet d'appartenance régionale n'est pas significatif dans notre exemple

L'analyse de la variance est une solution rigoureuse sur le plan statistique, mais elle est assez abstraite et ne laisse aucune liberté dans le choix de la mesure de dissimilarité. En effet, l'utilisation de l'analyse de la variance revient (implicitement) à mesurer les dissimilarités entre les lieux à l'aide du critère DSij = (Xi-Xj)² . Or, on peut souhaiter mesurer les dissimilarités à l'aide d'autres critère (Cf. document 1). Il existe une manière plus simple et plus générale pour mesurer les effets d'appartenance

1ere étape : Définition d'une matrice de dissimilarité
 

i	Xi				DSij	1	2	3	4	5	6	7	8	9
1	15				1	-	10	10	25	5	45	5	5	15
2	5				2	10	-	20	35	15	55	5	15	25
3	25				3	10	20	-	15	5	35	15	5	5
4	40				4	25	35	15	-	20	20	30	20	10
5	20				5	5	15	5	20	-	40	10	0	10
6	60				6	45	55	35	20	40	-	50	40	30
7	10				7	5	5	15	30	10	50	-	10	20
8	20				8	5	15	5	20	0	40	10	-	10
9	30				9	15	25	5	10	10	30	20	10	-

2^e étape : Définition d'une matrice d'appartenance commune
 

i	Ai				Aij	1	2	3	4	5	6	7	8	9
1	A				1	-	1	1	0	0	0	0	0	0
2	A				2	1	-	1	0	0	0	0	0	0
3	A				3	1	1	-	0	0	0	0	0	0
4	B				4	0	0	0	-	1	1	0	0	0
5	B				5	0	0	0	1	-	1	0	0	0
6	B				6	0	0	0	1	1	-	0	0	0
7	C				7	0	0	0	0	0	0	-	1	1
8	C				8	0	0	0	0	0	0	1	-	1
9	C				9	0	0	0	0	0	0	1	1	-

3^e étape : Calcul de la dissemblance moyenne en fonction de l'appartenance commune

• pour 2 lieux quelconques la dissemblance moyenne est DS_Tot =19.2
• pour 2 lieux de la même région (Aij=1), la dissemblance moyenne est DS_Intra = 17.8
• pour 2 lieux de régions différentes (Aij=0) la dissemblance moyenne est DS_Inter = 19.6

G = 1 - (DS_Intra / DS_Inter)

Si G>0 , l'autocorrélation territoriale est positive, ce qui signifie que deux lieux appartenant à une même région se ressemblent plus que deux lieux appartenant à des régions différentes.

Si G<0 , l'autocorrélation territoriale est négative, ce qui signifie que deux lieux appartenant à une même région se ressemblent moins que deux lieux appartenant à des régions différentes.

Si G=0 , l'autocorrélation territoriale est nulle, ce qui signifie que deux lieux appartenant à une même région se ressemblent ni plus ni moins que deux lieux appartenant à des régions différentes

Dans notre exemple, G = 1 -(17.8/19.6) = +0.09 (très lègère autocorrélation territoriale positive)

Document 4 : Analyse des effets de voisinage

(a) Définition des effets de voisinage

On dit qu'il existe un effet de voisinage lorsque les lieux proches se ressemblent plus que les lieux éloignés. Plus généralement, on parle d'autocorrélation spatiale lorsqu'il existe une relation entre la proximité spatiale des lieux et leur degré de ressemblance ou de dissemblance. On peut distinguer trois situations typiques :

• L'autocorrélation spatiale est positive lorsque deux lieux proches se ressemblent plus (en moyenne) que deux lieux éloignés.
• L'autocorélation spatiale est nulle lorsque deux lieux proches se ressemblent ni plus ni moins (en moyenne) que deux lieux éloignés.
• L'autocorrélation spatiale est négative lorsque deux lieux proches se ressemblent moins (en moyenne) que deux lieux éloignés.

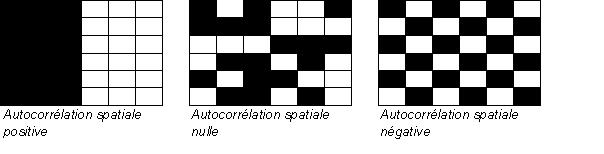
L'indice de Geary propose de mesurer l'autocorrélation spatiale à l'aide d'un indice qui est le rapport entre la variance des régions contiguës et la variance totale.

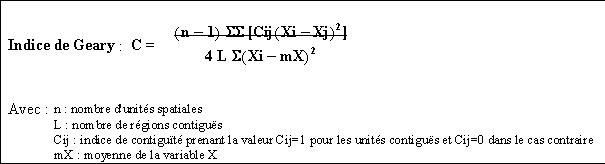
L'indice de Moran propose de mesurer l'autocorrélation spatiale à l'aide d'un indice qui est le rapport entre la covariance des régions contiguës et la variance totale.

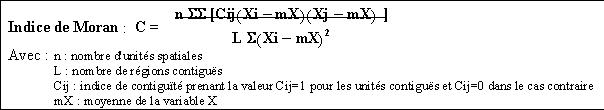
Ces deux indices sont assez compliqués, mais ils permettent d'effectuer des tests statistiques pour déterminer si l'effet de voisinage est imputable au hasard ou non.

(c) Une solution générale

On reprend l'exemple du document 3 et l'on cherche à déterminer s'il existe une relation entre la proximité spatiale des régions et leur degré de ressemblance :

1ere étape : Définition d'une matrice de dissimilarité

(Cf. document 3)

2^e étape : Définition d'une matrice de contiguïté
 

Cij	1	2	3	4	5	6	7	8	9
1	0	1	1	0	0	0	1	0	0
2	1	0	1	1	1	0	0	0	0
3	1	1	0	1	0	1	1	1	0
4	0	1	1	0	1	1	0	0	0
5	0	1	0	1	0	1	0	0	0
6	0	0	1	1	1	0	0	1	1
7	1	0	1	0	0	0	0	1	0
8	0	0	1	0	0	1	1	0	1
9	0	0	0	0	0	1	0	1	0

 

3^e étape : Calcul de la dissemblance moyenne en fonction de la contiguïté

• pour 2 lieux quelconques la dissemblance moyenne est DS_Tot =19.2
• pour 2 lieux proches (Cij=1), la dissemblance moyenne est DS_Prox = 19.7
• pour 2 lieux éloignés (Cij=0) la dissemblance moyenne est DS_Eloi = 18.7

Z= 1 - (DS_Prox / DS_Eloi)

Si Z>0 , l'autocorrélation territoriale est positive, ce qui signifie que deux lieux proches se ressemblent plus que deux lieux éloignés.

Si Z<0 , l'autocorrélation territoriale est négative, ce qui signifie que deux lieux proches se ressemblent moins que deux lieux éloignés.

Si Z=0 , l'autocorrélation territoriale est nulle, ce qui signifie que deux lieux proches se ressemblent ni plus nimoins que deux lieux éloignés

Dans notre exemple, Z = 1 -(17.8/19.6) = -0.05 (très lègère autocorrélation spatiale négative)
 
 

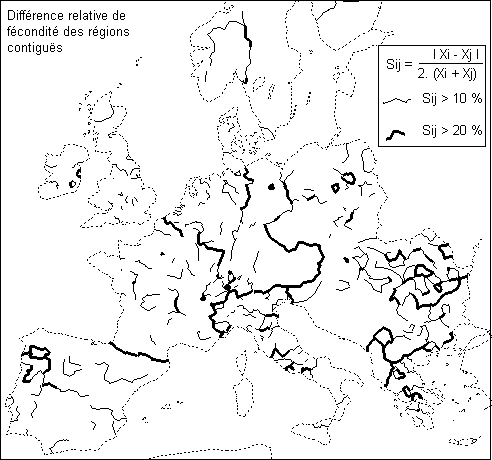
Document 5 : Application des méthodes d'analyse de l'autocorrélation spatiale et de l'autocorrélation territoriale
Source : Decroly J.M., Grasland C., (1993), "Frontières, systèmes politiques et fécondité en Europe", Espace Population Sociétés, 2, pp. 135-152
 
 

La fécondité des régions européennes en 1988

(a) Deux hypothèses

Hypothèse 1 : La fécondité d'une région européenne dépend de la fécondité de son pays d'appartenance. En effet, l'Etat dispose de nombreux moyens d'action (primes pour les familles nombreuses, lois interdisant l'avortement, etc.) qui peuvent contribuer à accroître ou réduire la fécondité.

• Si cette hypothèse est vraie, on devrait observer une autocorrélation territoriale positive (deux régions d'un même pays se ressemblent plus que deux régions de pays différents).

• Si cette hypothèse est vraie, on devrait observer une autocorrélation spatiale positive (deux régions contiguës se ressemblent plus que deux régions non contiguës).

(b) Choix du critère de dissimilarité

On a décidé de mesurer des différences relatives de fécondité exprimées en %

Dsij = abs(Xi-Xj) /moy(Xi , Xj)
 

 

		Non-voisines	Voisines	Ensemble
		Cij=0	Cij=1
Pays différents	Aij=0	26.0 %	18.3 %	26.0 %
Même pays	Cij=0	15.9 %	9.2 %	15.4 %
Ensemble		25.4 %	10.5 %	25.3 %

G= 1-(15.4/26.0) = +0.41

• L'autocorrélation territoriale est fortement positive : deux régions d'un même pays se ressemblent nettement plus que deux régions de pays différents

• L'autocorrélation spatiale est fortement positive : deux régions contiguës se ressemblent nettement plus que deux régions non contiguës

Une analyse plus approfondie des résultats montre que les deux effets se combinent ce qui entraîne l'apparition de discontinuités spatiales le long des frontières. Les différences de fécondité sont graduelles à l'intérieur des Etats alors qu'elles sont brutales de part et d'autre des frontières.