A DESCRIPTION D'UNE MATRICE DE FLUX

A.1) Définition d'une matrice de flux

• Lieux d'origines et de destination
• Période au cours de laquelle le flux est mesuré
• Nature du flux (personnes, marchandises, capitaux, énergie, information,…)
• Critère de quantification
• Mode de transport/transfert

• Résultats dérivés directement de la matrice des flux
• Autres indices

• Flux (F) / Volume (F+) / Solde (F-)
• Quantité / Intensité
• Méthode des flux dominants de Nyusten & Dacey

B.1) Historique

• Les lois de Ravenstein (1885-1889)
• L'analogie gravitaire (Reilly, Stewart, Zipf)
• Le dépassement de l'analogie gravitaire

• Effet des capacités d'émission et de réception
• Effet de la distance
• Effet de l'appartenance territoriale

C.1 Force d'attraction et zones d'influence théoriques

• La loi de Reilly
• Le modèle de Huff

• Opportunités de relation en fonction de la distance
• Le potentiel (Stewart)
• Formule général du potentiel

Document 1 : Les différents sens du mot "Interaction spatiale"

D'après C. Grasland, HYPERGEO : http://www.cybergeo.presse.fr/libergeo/hypergeo.htm

Bien qu’elle joue un rôle central dans la définition de la géographie contemporaine, la notion d’interaction spatiale est excessivement difficile à définir tant les définitions qui ont pu en être proposé sont variées. On peut toutefois tenter d’esquisser une classification de ces définitions afin de distinguer ce qui constitue le cœur de la notion , ce qui renvoie à des extensions de celle-ci et les problèmes théoriques qu’elle soulève.

(1) Interaction spatiale et modèle gravitaire

Une définition très fréquente dans la littérature anglo-saxonne réduit la notion d’interaction spatiale au phénomène de décroissance des flux avec la distance. L’observation des migrations à la fin du XIXe siècle a conduit très tôt différents auteurs à mettre en évidence des lois empiriques (Ravenstein) qui ont ensuite été rapprochées par analogie des lois de la gravitation universelle. Les modèles gravitaires qui font dépendre le volume d’interaction entre deux lieux de la masse des lieux émetteur et récepteur ainsi que de l’inverse du carré de la distance qui les séparent (Stewart) peuvent être considérés comme les précurseurs de formalisations théoriques plus générales des flux rassemblées actuellement sous le terme de modèles d’interaction spatiale.

(2) Modèles d'interaction et modèles de position

Si les modèles d’interaction spatialestricto sensu ont trait à l’étude des flux effectifs qui s’établissent entre des unités territoriales au cours d’une période de temps, de nombreux auteurs tendent à leur rattacher un ensemble de modèles de position (Fustier) qui décrivent non pas les relations entre deux lieux mais la position relative d’un lieu par rapport aux autres. Le calcul du potentiel d’un lieu se fonde certes sur la prise en compte d’une hypothèse d’interaction spatiale (forme de la décroissance de la probabilité de relation avec la distance) mais il s’agit fondamentalement d’une mesure d’accessibilité visant à évaluer la variation de la quantité d’opportunités de relation en fonction de la position. Les modèles de Reilly et de Huff qui visent à déterminer les aires de marché théoriques d’un ensemble de lieux centraux se rattachent également à la catégorie des modèles de position puisqu’ils visent à décrire les lieux (appartenance à une zone de marché) et non pas directement les relations entre les lieux.

(3) Interaction spatiale et interaction territoriale

Les premiers modèles d’interaction et de position ont longtemps postulé l’existence d’une relation mathématique simple entre l’éloignement physique des lieux (mesuré par une métrique continue) et le volume ou l’intensité des relations qui s’établissait ou qui pouvait s’établir entre eux. Les fonctions d’interaction spatiale les plus utilisées pour décrire l’influence de la distance demeurent les fonctions puissance négative (dites, de Paréto) et les fonctions exponentielles négatives.. Les phénomènes de barrière, qui sont en fait le signe de l’expression de l’influence de l’appartenance territoriale des lieux ont longtemps été considéré comme des exceptions au lois de l’interaction spatiale dont l’étude n’était envisagé que dans le cadre de l’analyse des résidus de ces modèles. Cette appartenance territoriale peut pourtant être considérée comme l’expression d’une mesure de proximité discrète dont l’expression la plus simple est une métrique booléenne prenant la valeur 0 si deux lieux appartiennent à la même maille territoriale et la valeur 1 si ils sont séparés par une limite de maille territoriale. On peut désigner sous le terme d’effet de barrière ou d'interaction territoriale le fait que, deux lieux appartenant à une même maille territoriale ont en moyenne plus de relation que deux lieux appartenant à deux mailles différentes. L’interaction territoriale apparaît alors comme une forme particulière de l’interaction spatiale définie plus généralement comme le fait que deux lieux spatialement proches ont en moyenne plus de relation que deux lieux spatialement éloignés.

(4) Interaction spatiale et relation spatiale

 
Pour de nombreux auteurs, la définition de l’interaction spatiale comme étude de l’influence de la proximité spatiale des lieux sur l’intensité des relations qui peuvent se constituer entre eux ne renvoie pas obligatoirement à l ‘étude des flux effectifs (modèles d’interaction) ou potentiels (modèles de position). Si l’on donne au terme relation un sens quelconque, la notion d’interaction spatiale peut aussi bien désigner l’existence de relations causales dans l’espace (ce qui se passe en un lieu exerce une influence sur ce qui passe dans les autres lieux et qui varie en fonction de leur proximité), l’existence de processus de diffusion spatiale (une innovation qui apparaît en un lieu à de fortes chances de se propager vers les lieux proches, que la proximité soit mesurée de façon continue ou de façon hiérarchique), voire l’existence de formes d’autocorrélation spatiale (i.e. le fait que deux lieux proches se ressemblent plus que deux lieux éloignés). Même s’il existe des liens logiques entre tous ces champs d’analyse (les flux peuvent être à l’origine de processus de diffusion qui engendrent des formes spatiales qui vont rétroagir sur l’intensité des flux, etc.) on peut penser qu’une définition aussi extensive de l’interaction spatiale reviendrait à en faire un synonyme du terme analyse spatiale voire de la géographie dans son ensemble.

(5) Interaction spatiale et relation sociale

L’expression de relations entre les lieux qui sous-tend l’ensemble des définitions proposées de l’interaction spatiale constitue sans nul doute un point d’achoppement central qui explique en grande partie les réactions hostiles qu’ont suscité et que suscitent encore les modèles d’interaction spatiale. Si cette notion de relation entre les lieux ne suscite pas de difficultés particulières en géographie physique, où elle peut renvoyer à des phénomènes concrets tels que le déplacement de masses d’air ou le transfert d’une charge solide par les cours d’eau, il n’en va pas de même en géographie humaine lorsque l’on prétend décrire des phénomènes sociaux à l’aide de lois globales du comportement humain. En géographie humaine, les relations entre lieux, qu’ils s’agissent de villes, de régions ou d’état ont en effet alors trait à des agrégats sociaux ou économiques localisés, le plus souvent hétérogènes, composés d’individus (personnes, ménages, entreprises,…) ne disposant pas des mêmes revenus, des mêmes capacités de mobilité, de la même information sur les opportunités de relation distantes. Les modèles d’interaction spatiale postulent alors, le plus souvent implicitement, une double hypothèse de pertinence des agrégats sociaux et économiques constitués et d’existence d’un comportement moyen permettant de résumer celui des individus qui composent ces agrégats. Plutôt que de considérer les phénomènes d’interaction spatiale comme une composante exogène du comportement social, il semble plus intéressant de considérer au contraire qu’elles en constituent une résultante globale qu’il est intéressant de considérer comme telle. Les justifications les plus pertinentes des modèles d’interaction spatiale sont précisément celles qui démystifient l’effet de la distance et rattachent son influence à des processus économiques (Reilly), sociologiques (Stouffer) ou cognitifs (Hägerstrand).

Document 2 : La description d'une matrice de flux

A partir d'une enquête effectuée par la Direction des Etudes et de la Prospective (DEP) du ministère de l'Education Nationale et de l'Enseignement Supérieur (MESR), on peut connaître l'évolution de la localisation des étudiants français du supérieur entre les rentrées de 1993 et 1994. Même si cette localisation est connue avec une certaine incertitude (un étudiant peut être inscrit à l'Université de Rennes mais suivre les cours dans une antenne universitaire située dans une autre ville de Bretagne), l'enquête permet de reconstituer assez bien les déplacements des étudiants entre les villes françaises au cours de la période 1993-1994, surtout si on se limite aux plus grandes d'entre elles.
 
 

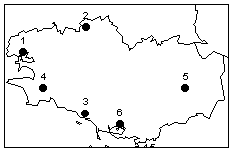
(1) Définition des unités étudiées : 6 villes universitaires de Bretagne
 

n°	Ville		Population de l'agglomération en 1991 (en hab.)
1	BREST		201 000
2	LANNION		20 000
3	LORIENT		115 000
4	QUIMPER		66 000
5	RENNES		245 000
6	VANNES		46 000

(2) Définition de la matrice des flux : migrations d'étudiants (rentrée 1993 - rentrée 1994)
 

				vers	(j)
	Fij	BRE	LAN	LOR	QUI	REN	VAN	Oi
	BRE	-	19	10	54	369	14	466
	LAN	40	-	4	0	48	6	98
de	LOR	19	0	-	2	6	2	29
(i)	QUI	67	0	0	-	29	9	105
	REN	190	62	5	21	-	70	348
	VAN	8	1	0	0	56	-	65
	Dj	324	82	19	77	508	101	1111

 

(3) Analyse des marges de la matrice des flux
 

i	Ville	Départs	Arrivées	Volume	Solde	Attractiv.
		(O)	(D)	V=(O+D)	S=(D-O)	A=(S/V)
1	BREST	466	324	790	-142	-18%
2	LANNION	98	82	180	-16	-9%
3	LORIENT	29	19	48	-10	-21%
4	QUIMPER	105	77	182	-28	-15%
5	RENNES	348	508	856	160	19%
6	VANNES	65	101	166	36	22%

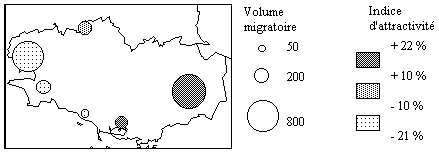
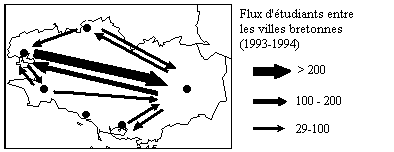
(4) Analyse des couples Origine-Destination

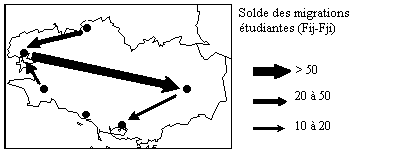
(4-a)Cartographie des 10 principaux flux migratoires

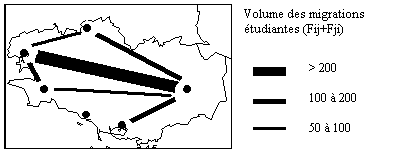
(4-b) Volume et solde des échanges d'étudiants entre les villes bretonnes (1993-1994)
 

F+	BRE	LAN	LOR	QUI	REN	VAN	Tot
BRE	0	59	29	121	559	22	790
LAN	59	0	4	0	110	7	180
LOR	29	4	0	2	11	2	48
QUI	121	0	2	0	50	9	182
REN	559	110	11	50	0	126	856
VAN	22	7	2	9	126	0	166
Tot	790	180	48	182	856	166	2222

F-	BRE	LAN	LOR	QUI	REN	VAN	Tot
BRE	0	-21	-9	-13	179	6	142
LAN	21	0	4	0	-14	5	16
LOR	9	-4	0	2	1	2	10
QUI	13	0	-2	0	8	9	28
REN	-179	14	-1	-8	0	14	-160
VAN	-6	-5	-2	-9	-14	0	-36
Tot	-142	-16	-10	-28	160	36	0

(4-c) Profils d'émigration et d'immigration
 

Fij/Oi	BRE	LAN	LOR	QUI	REN	VAN	tot
BRE	0%	4%	2%	12%	79%	3%	100%
LAN	41%	0%	4%	0%	49%	6%	100%
LOR	66%	0%	0%	7%	21%	7%	100%
QUI	64%	0%	0%	0%	28%	9%	100%
REN	55%	18%	1%	6%	0%	20%	100%
VAN	12%	2%	0%	0%	86%	0%	100%

Fij/Dj	BRE	LAN	LOR	QUI	REN	VAN
BRE	0%	23%	53%	70%	73%	14%
LAN	12%	0%	21%	0%	9%	6%
LOR	6%	0%	0%	3%	1%	2%
QUI	21%	0%	0%	0%	6%	9%
REN	59%	76%	26%	27%	0%	69%
VAN	2%	1%	0%	0%	11%	0%
tot	100%	100%	100%	100%	100%	100%

(4-d) Flux dominants

METHODE NYUSTEN & DACEY : i est dominé par j si :

1. i envoie son flux le plus important vers j
2. La somme des arrivées de j est plus importante que la somme des arrivées de i

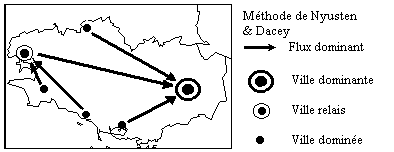
VARIANTE : i est dominé par j si :

1. i envoie k % de ses migrants vers j
2. La somme des arrivées de j est plus importante que la somme des arrivées de i

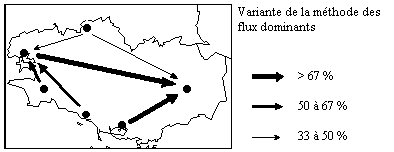
Document 3 : Historique du modèle gravitaire

(A) FIN XIXe : LES LOIS DE RAVENSTEIN
(Ravenstein E., 1885 & 1889, "The Laws of Migration", Journal of Royal Statist. Society, London)

1. Le nombre de migrants diminue quand la distance augmente; la plupart ne vont pas très loin ; ceux qui se déplacent sur de grandes distances se dirigent de préférence vers les grands centres commerciaux et industriels.
2. Le processus se fait de la façon suivante : une ville à croissance rapide attire les gens des régions environnantes ; les vides ainsi créés sont comblés par les migrants de districts plus éloignés ; la force d'attraction des grandes villes dynamiques se fait donc sentir de proche en proche en diminuant d'intensité. Le nombre de migrants de la zone d'accueil est donc proportionnel à la population de la zone d'origine et inversement proportionnel à la distance qui les sépare.
3. Chaque courant principal de migration suscite un contre-courant compensatoire.
4. Les citadins ont une mobilité plus faible que les ruraux
5. Les femmes ont une mobilité plus forte que les hommes, au moins à courte distance.
6. L'intensité des migrations augmente avec le développement du commerce, de l'industrie et des transports.
7. Les facteurs déterminant la migration sont nombreux mais le plus important est le facteur économique

(B) DEBUT XXe : L'ANALOGIE GRAVITAIRE (PARETO, STEWART)

Sous des formes voisines, plusieurs auteurs proposent de transposer aux migrations humaines la loi de la gravitation universelle de Newtown :
 

Modèle de Newtown Aij = g . Mi . Mj / Dij 2 Aij : force d'attraction entre i et j g : constante gravitaire universelle Mi, Mj : masse des planètes Dij : distance entre les planètes

Modèle de Stewart Fij = k . Pi . Pj / Dij 2 Fij : nombre de migrants de i vers j k : niveau global de mobilité Pi, Pj : population des lieux i et j Dij : distance entre les lieux i et j

 
 
 

Les auteurs suivants introduisent des modification et proposent plusieurs variantes

Fij = k . (Pi)^b1 . (Pj)^b2 . (Dij) ^-a: modèle gravitaire généralisé (Paréto)

Fij = k . (Pi)^b1 . (Pj)^b2 . exp ^{-a Dij} : modèle gravitaire généralisé (exponentiel)

Fij = ai.Oi. bj. Dj. ^{-a Tij} : modèle entropique de Wilson

Fij = (Ai+Bj)/Dij : modèle additif de Tobler

(C) FIN XXe : LA REMISE EN CAUSE DE L'ANALOGIE GRAVITAIRE

De nombreux auteurs n'acceptent pas la transposition au comportement humain des lois de la physique et tentent d'expliquer autrement la décroissance des interactions avec la distance :

1. L'explication économique (ZIPF) : L'effet de la distance doit s'interpréter comme l'ajustement de l'offre et de la demande de mobilité en fonction du coût de déplacement. La distance n'agit que si elle est proportionnelle au coût de mise en relation. Les acteurs obéissent au principe du moindre effort (rationalité économique).
2. L'explication sociologique (S. STOUFFER) : Plus la distance augmente, plus le nombre d'occasions interposées (intervening opportunities) est élevé. Ce n'est donc pas la distance qui agit directement mais la population du fait que le migrant trouve d'autres occasions de migrer entre son lieu de départ et son lieu d'arrivée.
3. L'explication psychologique (T. HAGERSTRAND) : Toute migration est précédée d'un flux d'information (connaissance du lieu de destination). La décroissance des migrations avec la distance est liée à l'ignorance des migrants sur les lieux de destination éloignés.

Document 4 : Reconstruction hypothético-déductive du modèle gravitaire

(A) Description des données

Carte 1 : Organisation administrative de la Tchécoslovaquie en 1989

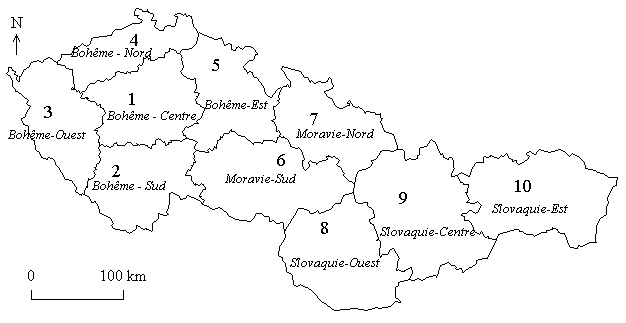
Tableau 1 : Population des régions de Tchécoslovaquie en 1989
 

i	Code	Région	République	Population
1	BC	Bohême-Centre	Tchèque	2 333 670
2	BS	Bohême-Sud	Tchèque	698 568
3	BO	Bohême-Ouest	Tchèque	869 445
4	BN	Bohême-Nord	Tchèque	1 190 781
5	BE	Bohême-Est	Tchèque	1 239 979
6	MS	Moravie-Sud	Tchèque	2 058 234
7	MN	Moravie-Nord	Tchèque	1 971 580
8	SO	Slovaquie-Ouest	Slovaque	2 164 548
9	SC	Slovaquie-Centre	Slovaque	1 611 930
10	SE	Slovaquie-Est	Slovaque	1 499 708
		Tchécoslovaquie		15638443

Tableau 2 : Migrations inter-régionales de population en Tchécoslovaquie en 1989
 

						vers
		BC	BS	BO	BN	BE	MS	MN	SO	SC	SE	Total
	BC		2096	1792	3025	2411	1110	793	395	284	282	12188
	BS	2420		756	543	360	853	348	153	91	106	5630
	BO	2635	1081		1312	399	553	369	213	211	146	6919
	BN	4120	1073	1542		1406	648	535	220	183	292	10019
de	BE	3530	610	471	1275		1210	781	211	141	122	8351
	MS	2187	1337	669	702	1267		2643	707	338	239	10089
	MN	1852	593	662	682	1017	3143		599	623	370	9541
	SO	668	177	249	225	226	737	559		3126	732	6699
	SC	524	168	266	251	188	396	801	3839		1229	7662
	SE	769	206	292	534	302	444	689	1567	1487		6290
	Total	18705	7341	6699	8549	7576	9094	7518	7904	6484	3518	83388

Carte 2 : Principaux flux migratoires entre les régions tchécoslovaques en 1989

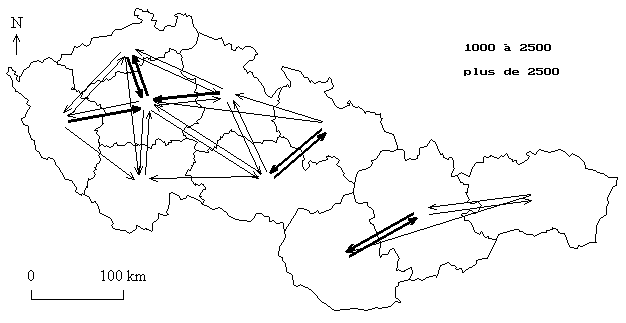
(B) MODELE 1 : EFFET DES CAPACITES D'EMISSION ET DE RECEPTION

Hypothèse :

Plus une région est peuplée, plus elle peut envoyer de migrants vers les autres régions

Plus une région est peuplée, plus elle peut attirer des migrants venant d'autres régions

MODELE 1 : Fij = k. Pi . Pj avec k = S iS j Fij / S iS j PiPj

Ajustement :

La constante (k) du modèle d'interaction élémentaire est obtenue facilement en divisant la somme des flux par la somme du produit des populations pour l'ensemble des paires de régions. Dans l'exemple tchécoslovaque on trouve :

S iS j Fij = 83388 (nombre de migrants)

S iS j PiPj = 2.17 x 10¹⁴ (nombre de paires d'habitants localisés dans des régions différentes)

donc k = 3.84 x 10^-10

Analyse des résidus :

Ce premier modèle apparaît peu satisfaisant et il laisse apparaître des résidus très important. Si l'on considère par exemple les migrations au départ de la Bohême-Centre, on constate que notre modèle sous-estime les migrations de cette région vers les reste de la Bohême (résidus positifs) et sur-estime les migrations vers la Moravie et surtout la Slovaquie (résidus négatifs). Ces résidus traduisent évidemment l'oubli d'un facteur majeur : la distance.
 

de BC vers …	BS	BO	BN	BE	MS	MN	SO	SC	SE	total
Flux observé	2096	1792	3025	2411	1110	793	395	284	282	12188
Flux théorique	626	779	1067	1111	1844	1766	1939	1444	1343	11917
Résidu	1470	1013	1958	1300	-734	-973	-1544	-1160	-1061	271

Le MODELE 1 serait vrai si l'intensité des flux (Fij/PiPj) était constante. Or ce n'est pas le cas : l'intensité des flux varie en fonction de la distance.
 
 

Figure 1: Relation entre intensité des flux et distance

(a) Graphique arithmétique (b) Graphique bi-logarithmique

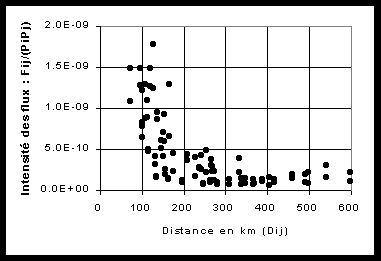
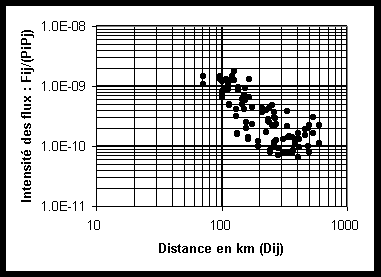
On remarque que l'intensité des flux est une fonction non-linéaire de la distance. Des tests montrent que le meilleur ajustement est obtenu dans un repère bi-logarithmique ce qui signale l'existence d'une relation de type puissance (dans certains cas, le meilleur ajustement serait obtenu pour un repère semi-logarithmique ce qui indiquerait une relation exponentielle).

(C) MODELE 2 : EFFET DE LA DISTANCE (INTERACTION SPATIALE)

Hypothèse :

Toutes choses égales quant à leurs capacités d'émission ou de réception, les régions proches échangent plus de migrants que les régions éloignées. L'intensité des migrations diminue avec la distance selon une fonction puissance

En effet : log[Fij/(PiPj)] = a.log(Dij) + b (d'après le graphique bi-logarithmique)

ó Fij/ PiPj = exp[a.log(Dij) +b]

ó Fij = exp(b) . Pi . Pj . (Dij)^a(on retrouve le modèle gravitaire !)

MODELE 2 : Fij = k. Pi . Pj . (Dij)^-aavec k= S iS j Fij / S iS j [Pi . Pj .(Dij)^-a]

Ajustement :

On calcule les valeurs de Y = log[Fij/(PiPj)] et de X = log(Dij)

On effectue une régression linéaire Y = -1.31X -14.9 (r² = 57%)

On en déduit l'équation du MODELE 2 : Fij = 3.34 . 10^-7 . Pi . Pj . Dij ^-1.31

Analyse des résidus :

On déduit de notre équation précédente les flux théoriques F*ij qui devraient être observés si les flux ne dépendaient que de la population des régions et de la distance qui les sépare.

Tableau 3 : Migrations estimées par le modèle gravitaire
 

F*ij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE	Total
BC		1389	1498	3548	2344	1874	1279	944	560	347	13782
BS	1389		366	352	413	668	355	345	179	106	4172
BO	1498	366		662	335	407	290	260	154	102	4075
BN	3548	352	662		806	649	529	378	241	159	7327
BE	2344	413	335	806		1725	1396	673	422	243	8357
MS	1874	668	407	649	1725		3250	2479	1120	512	12685
MN	1279	355	290	529	1396	3250		1840	1450	646	11034
SO	944	345	260	378	673	2479	1840		2415	778	10112
SC	560	179	154	241	422	1120	1450	2415		1205	7747
SE	347	106	102	159	243	512	646	778	1205		4097
Total	13782	4172	4075	7327	8357	12685	11034	10112	7747	4097	83388

On peut alors calculer la matrice des résidus du modèle d'interaction spatiale en effectuant la différence entre flux observés et flux théoriques : Rij=Fij-F*ij

Tableau 4 : Résidus des migrations estimées par le modèle gravitaire
 

Rij	BC	BS	BO	BN	BE	MS	MN	SO	SC	SE	Total
BC	0	707	294	-523	67	-764	-486	-549	-276	-65	-1594
BS	1031	0	390	191	-53	185	-7	-192	-88	0	1458
BO	1137	715	0	650	64	146	79	-47	57	44	2844
BN	572	721	880	0	600	-1	6	-158	-58	133	2692
BE	1186	197	136	469	0	-515	-615	-462	-281	-121	-6
MS	313	669	262	53	-458	0	-607	-1772	-782	-273	-2596
MN	573	238	372	153	-379	-107	0	-1241	-827	-276	-1493
SO	-276	-168	-11	-153	-447	-1742	-1281	0	711	-46	-3413
SC	-36	-11	112	10	-234	-724	-649	1424	0	24	-85
SE	422	100	190	375	59	-68	43	789	282	0	2193
Total	4923	3169	2624	1222	-781	-3591	-3516	-2208	-1263	-579	0

Marges de la matrice des résidus

L'analyse des marges de la matrice des résidus permet de repérer les régions qui ont globalement reçu ou envoyés plus (ou moins) de migrants que ce que laissait prévoir le modèle. On peut en déduire des coefficients de mobilité résiduelle ou d'attractivité résiduelle.

Tableau 5 : Analyse des marges de la matrice des résidus
 

i	Emissions	Reception	Mobilité	Attractivité
BC	-1594	4923	3328	6517
BS	1458	3169	4626	1711
BO	2844	2624	5468	-220
BN	2692	1222	3915	-1470
BE	-6	-781	-786	-775
MS	-2596	-3591	-6187	-995
MN	-1493	-3516	-5010	-2023
SO	-3413	-2208	-5620	1205
SC	-85	-1263	-1347	-1178
SE	2193	-579	1613	-2772

Flux résiduels

L'analyse des flux résiduels proprement dit permet de repérer les régions qui entretiennent des relations préférentielles (résidus positifs) et celles qui sont au contraire séparées par des effets de barrière (résidus négatifs).

Carte des plus forts résidus positifs Carte des plus forts résidus négatifs

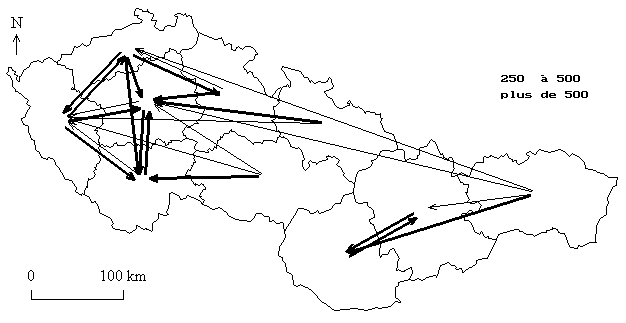
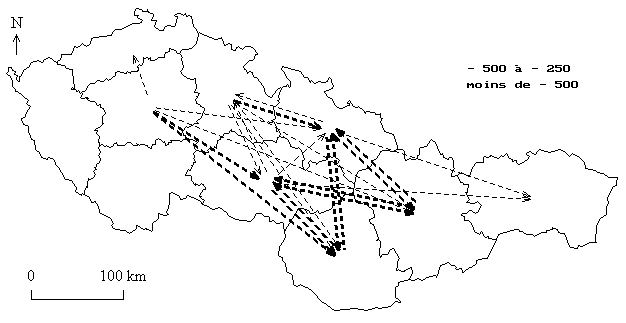
Résidus agrégés par républiques
 

Fij	S	T	Total		Aij	Fij
S	11980	8671	20651		1	68791
T	5926	56811	62737		0	14597
Total	17906	65482	83388		Total	83388
F*ij	S	T	Total		Aij	F*ij
S	8794	13161	21955		1	57065
T	13161	48271	61433		0	26323
Total	21955	61433	83388		Total	83388
Fij/F*ij	S	T	Total		Aij	Fij/F*ij
S	1.36	0.66	0.94		1	1.21
T	0.45	1.18	1.02		0	0.55
Total	0.82	1.07	1.00		Total	1.00

 
 
 
 
 

(D) MODELE 3 : EFFET DE L'APPARTENANCE (INTERACTION TERRITORIALE)

Hypothèse :

Toutes choses égales quand à leurs populations et à la distance qui les sépare, les régions d'une même république (Aij=1) échangent plus de migrants que les régions localisées dans des républiques différentes (Aij=0). L'accroissement relatif des flux intra-républiques par rapport aux flux inter-républiques correspond à la valeur de l'effet de barrière (g )
 
 

MODELE 3 : Fij = k. Pi . Pj . (Dij)^-a. g^Aij
 

Ajustement :

• Les flux inter-républiques sont plus faibles que prévus car le coefficient d'interaction territoriale associé aux échanges inter-républiques est inférieur à 1 : b_Inter = 0.55.
• Les flux intra-républiques sont plus forts que prévus car le coefficient d'interaction territoriale associé aux échanges intra-républiques est supérieur à 1 : b_Intra = 1.21.
• La valeur de l'effet de barrière combine les deux effets précédents et exprime l'accroissement relatif des flux intra-républiques par rapport aux flux inter-républiques

• On peut en déduire la perméabilité de la frontière tchéco-slovaque qui est l'inverse du coefficient de barrière :

Conclusion :

En Tchécoslovaquie, les migrations dépendent d'au moins trois facteurs :

• la population des régions d'origine et de destination,
• la distance qui les sépare,
• le fait qu'elles soient localisés ou non dans la même république.

Pour plus de détails se reporter aux articles suivants :

Cattan N., Grasland C., 1994, " Migrations et effets de barrière en Tchécoslovaquie " , in Rey V. (ed.), La Tchécoslovaquie en 1992 : transition, fragmentation, recomposition, Presses de l'ENS Fontenay-Saint-Cloud, coll. Sociétés, Espaces, Temps, 97-120

Grasland C., 1994, " Limites politiques et barrières migratoires : l'exemple de l'ex-Tchécoslovaquie (1965-1989) ", in Galluser W. (ed.), Political Boundaries and Coexistence, IGU Symposium, Basle, May 1994, 425-440

Document 5 : Les trois hypothèses fondamentales pour comprendre et modéliser les flux

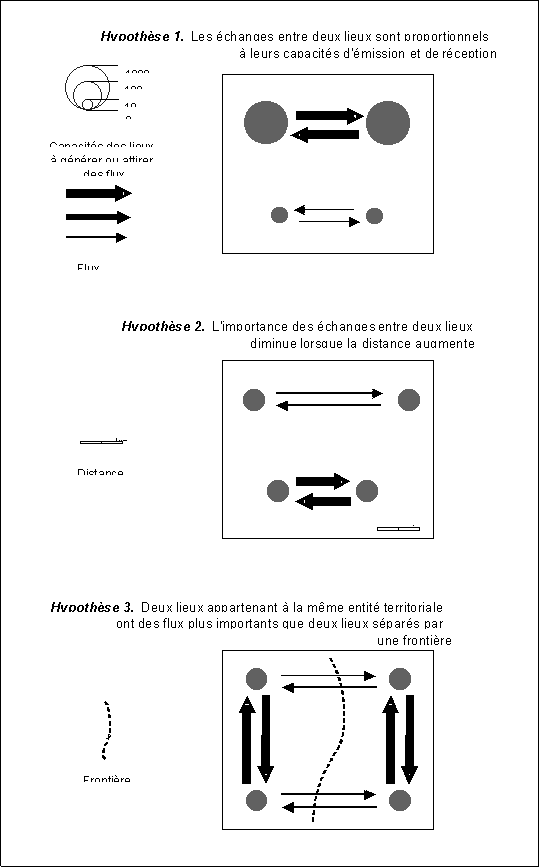
Document 6 : La loi de Reilly et ses variantes
 

(A) Formulation initiale de la loi de Reilly

 
 
 

Pour Reilly, la force d'attraction exercée par une ville j sur un lieu i est proportionnelle à sa taille (M_j) et inversement proportionnelle au carré de la distance (D_ij) qui sépare i et j.



Application : Les habitants d'Arras seront-ils davantage attirés par Paris (10 millions d'habitant , 150 km) ou par Lille (1 millions d'habitants, 50 km) ?

A _{Arras -> Paris} = 10 000 000 / (150)² = 444

A _{Arras -> Lille} = 1 000 000 / (50)² = 400

On en conclue que l'attraction de Paris sur Arras est plus forte que celle de Lille.

Reilly montre ensuite que l'on peut déduire de sa formule le point d'équilibre O entre les aires d'influences de deux villes a et b situées à une distance Dab, et de tailles respectives M_a et M_b :



Application : la distance entre Paris (a) et Lille (b) étant de 200 km, on peut montrer que le point d'équilibre entre leurs aires d'influences se situe à 200 / (1+Ö 0.1) = 152 km de Paris. On peut aussi le démontrer graphiquement en calculant les courbes décrivant les forces d'attraction respectives de Lille et Paris :

 
On s'est rapidement rendu compte que l'exposant de la distance dans loi de Reilly devait être adaptée selon le type d'aires d'influence que l'on souhaite construire. Pour les services courants, la distance compte davantage que l'offre (exposant supérieur à 2) tandis que pour les services rares, l'offre compte plus que la distance (exposant inférieur à 2). D'où la formule générale :

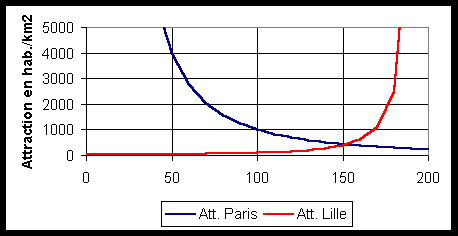
Plusieurs auteurs ont critiqué le caractère déterministe de la loi de Reilly qui suppose que les consommateurs sont des homo economicus pleinement informés et rationnels. Plutôt que de correspondre à des lignes précises, les limites des aires d'influences doivent correspondre à des zones de transition plus ou moins floues. HUFF qui travaillait sur l'attraction des centres commerciaux a proposé une formulation probabiliste de la loi de Reilly qui permet de modéliser la part de marché que détiennent théoriquement différents centres concurrents en chaque point d'un territoire donné. Le problème de Huff peut se formuler ainsi :

Le problème de Huff :

Soit un ensemble de k centres concurrents 1..j..k de masses respectives M₁..M_j…M_k

Soit un consommateur localisé en un point i situé à des distances D_1i ..D_ij …D_ik de ces centres.

Quelle est la probabilité p_ij pour le consommateur localisé en i de fréquenter le centre j ?

• Chaque centre commercial j représente pour le consommateur une opportunité que l'on peut évaluer par la formule de Reilly : O_ij = M_j / (D_ij)a
• Le potentiel de relations pour un consommateur localisée en i est égale à la somme de toutes les opportunités de destination : Pot_i = S_k O_ik
• La probabilité de choisir une destination est égale à l'opportunité de cette destination divisée par la somme totale des opportunités de destination : p_ij = Oij / S_k O_ik

Quatre centres urbains desservent une région de Transvodkavie.

Quelles sont leurs aires d'influence respectives ?
 

Centre	Surface	Localisation
	commerciale (m2)	X	Y
Triffouilly	100000	2.5	2.5
Klug	50000	4.5	6.5
Dhoubi	20000	12.5	2.5
Tchou	20000	12.5	8.5

L'application de la loi de Huff permet de répondre à la question et de repérer les zones exclusives (où un centre domine) et les zones d'indifférence (où une publicité bien ciblée permettra d'attirer de nouveaux clients).

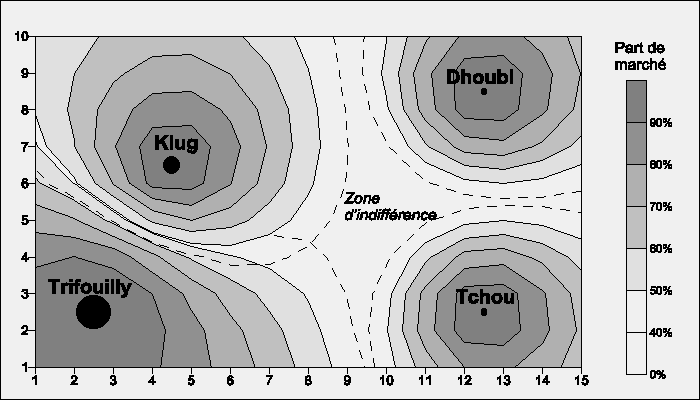
Document 7 : Le potentiel de population de Stewart

D'un point de vue économique, le problème posé par Stewart est plus ou moins l'inverse de celui de Reilly. Au lieu de déterminer les aires de marché en fonction de la localisation des centres (modélisation de l'offre), on va chercher à déterminer la localisation optimale des centres en fonction de la localisation des consommateurs (modélisation de la demande).

Exemple : On souhaite installer un café en A ou en B. On suppose qu'il n'y a pas de concurrence mais que les habitants hésitent à faire de longs déplacements. Quelle localisation attirera le plus de clients ?

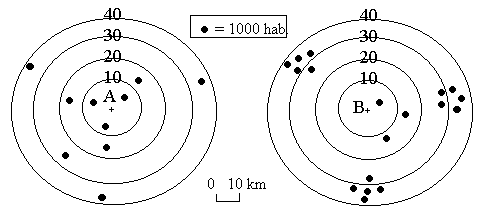
Population en fonction de la distance
 

Distance	Population		Population cumulée
	A	B	A	B
[0 ; 10[	3000	1000	3000	1000
[10 ; 20 [	3000	2000	6000	3000
[20 ; 30[	1000	4000	7000	7000
[30 ; 40 [	3000	11000	10000	18000

Tout le problème du choix tourne autour de la portée des déplacements que les personnes sont disposées à franchir : En A il y a moins d'habitants mais ils sont proches, tandis qu'en B il y a plus d'habitants mais ils sont plus éloignés. Si les habitants sont peu mobiles il vaut mieux s'installer en A, sinon il faut s'installer en B.

Si l'on admet que les déplacements obéissent au règle de l'interaction spatiale, ils doivent décroître en fonction de la distance. On pourra donc estimer le potentiel d'un lieu en effectuant la somme des populations divisées par la distance :

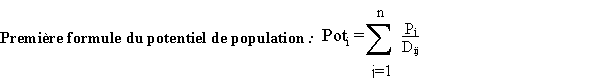
Exemple : on assimile chaque classe de distance à son centre [0; 10[ = 5 ; [10;20[ = 15 ; etc. et on calcule :

Potentiel de A = (3000/5 ) + (3000/15) + (1000/25) + (3000/35) = 925.7

Potentiel de B = (1000/5) + (2000/15) +(4000/25) + (11000/35) = 807.6

Donc, si l'on suit les hypothèses de Stewart, il vaut mieux s'installer en A car le potentiel y est plus fort.

Toutefois, rien ne prouve que la décroissance des relations avec la distance suive une loi du type 1/Dij et l'on peut proposer une formule plus générale que celle de Stewart :

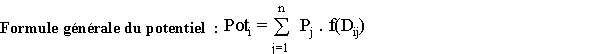
ou f est une fonction quelconque de la distance ( de type puissance, exponentielle, etc.)

Document 8 : Exemples d'application du potentiel de population

Source : C. Grasland, 1999, Seven proposals for the construction of geographical position indexes, Study Program on European Spatial Planning, Working Paper from SDEC-France, 30 p.
 

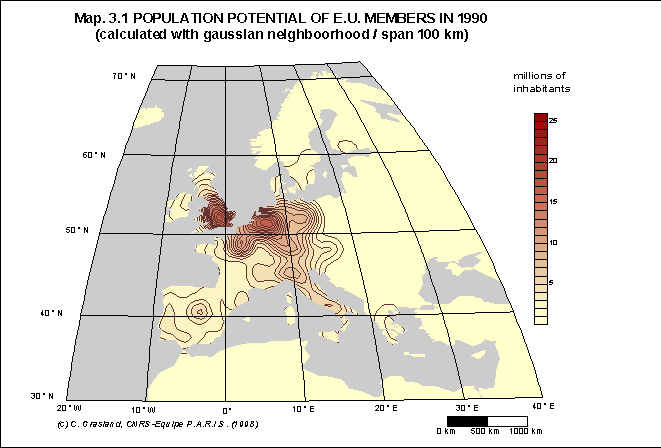
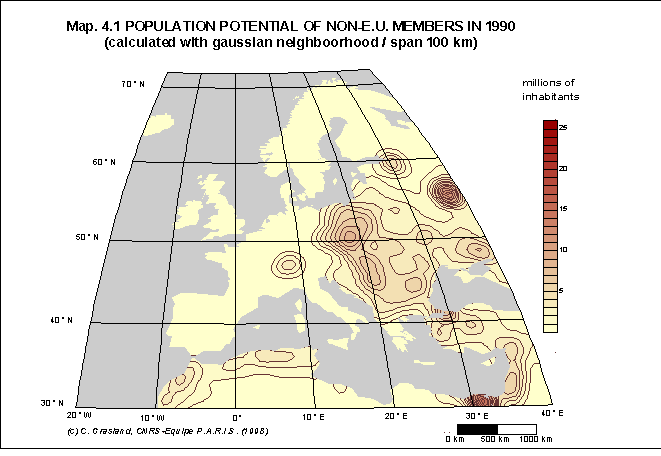
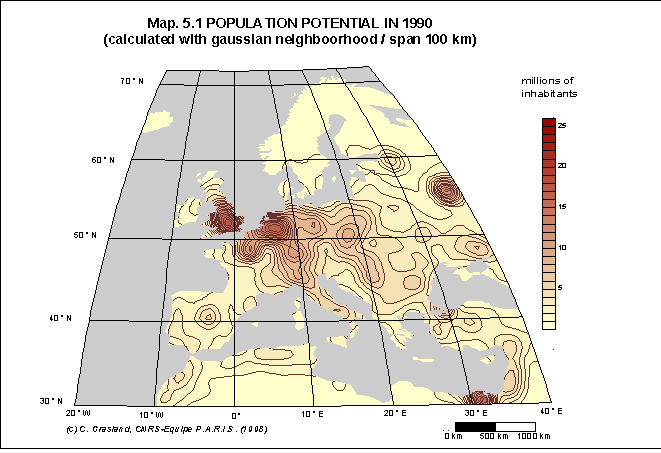
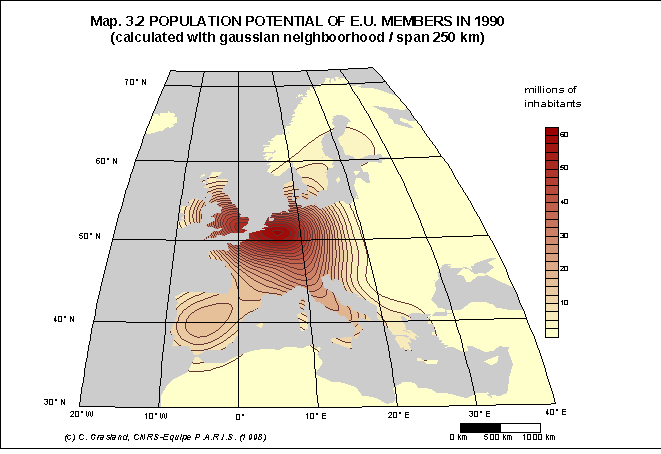
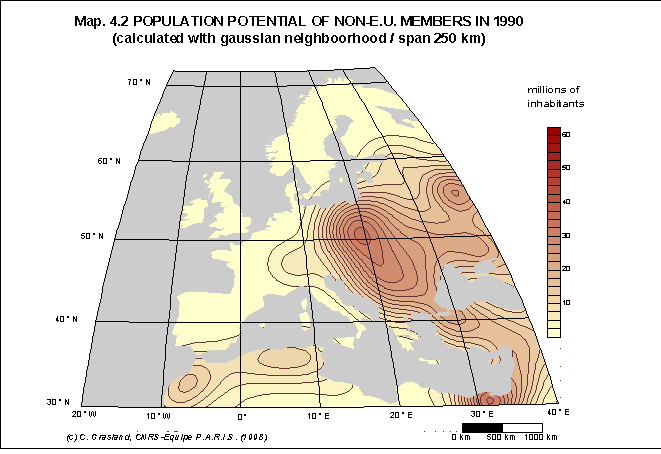
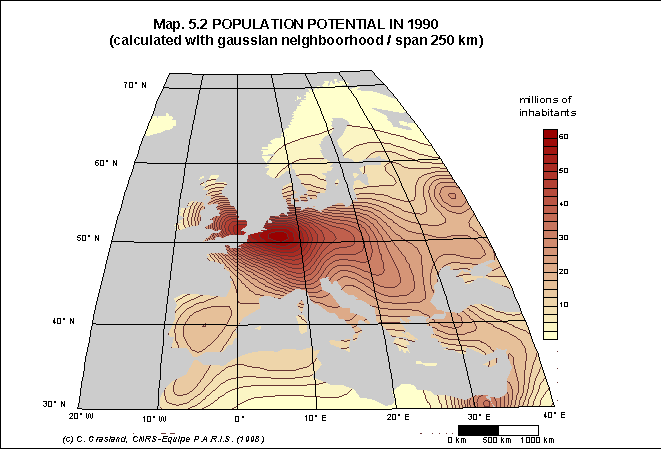
Dans cette étude réalisée pour le compte de l'Union Européenne, on a tenté d'examiner les changements de la configuration du potentiel de population en Europe en fonction de deux hypothèses :

1. Accroissement de la mobilité : en utilisant une fonction d'interaction spatiale f(Dij) dont la portée moyenne est de 100 km ou de 250 km
2. Ouverture des frontières : en calculant le potentiel de population de l'Union Européenne et des pays extérieurs de façon séparée puis en les additionnant.