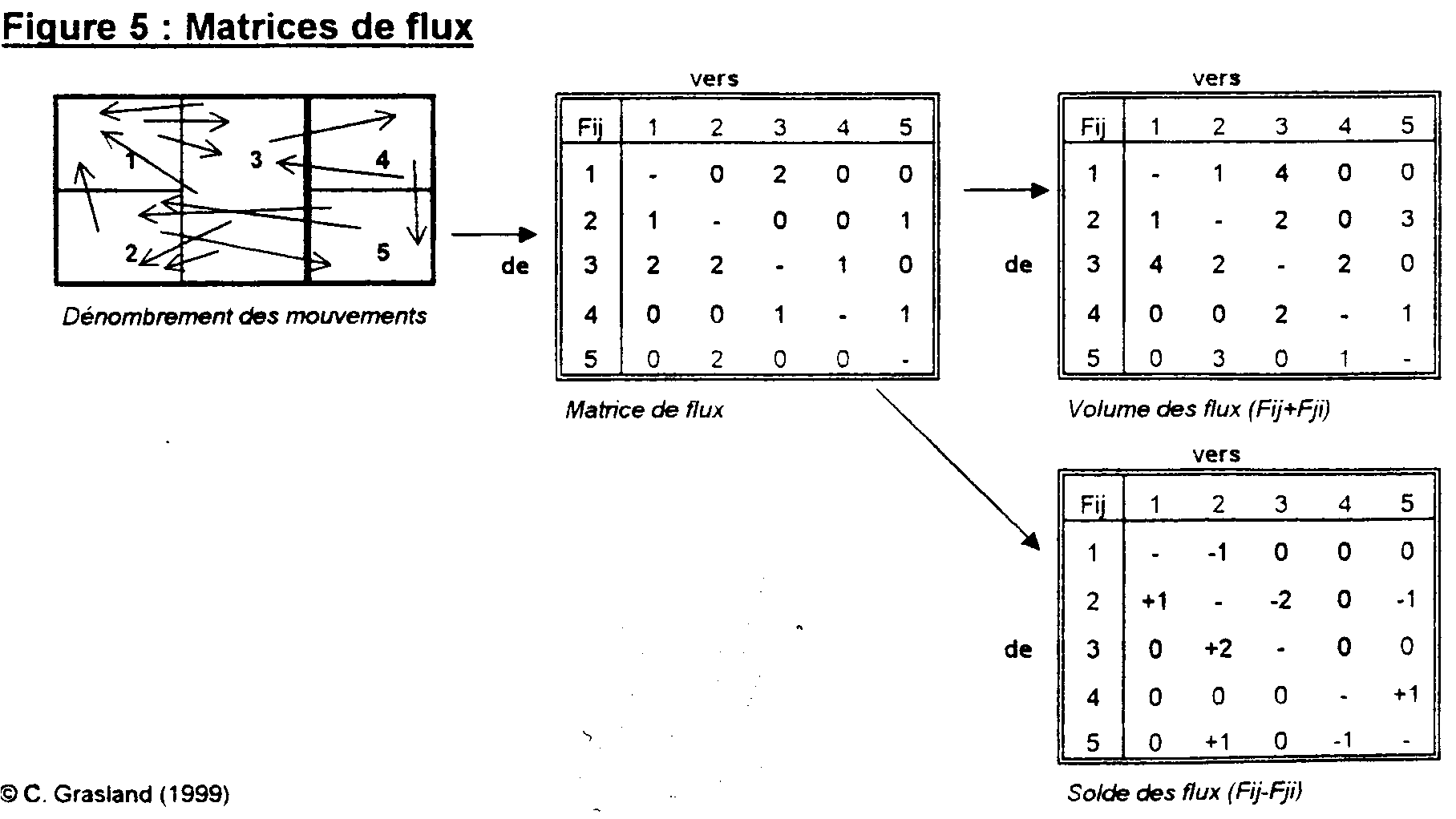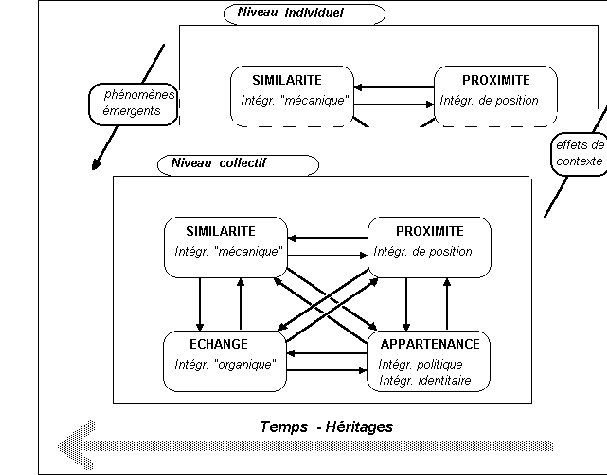
Source : Hugonie G., Géographie-Lycée. Aide à la mise en œuvre des programmes, CNDP/CRDP de Versailles, 1991, p. 15
|
Analyse spatiale et modélisation des phénomènes géographiques Claude Grasland
|
PLAN DU CHAPITRE
A.1) Critères de scientificité
B. LA RECHERCHE DE LOIS EN GEOGRAPHIE
B.1) L'espace impose des contraintes au fonctionnement des sociétés …
C. QU'EST-CE QUE L'ANALYSE SPATIALE ?
C.1) L'analyse statistique étudie les attributs des lieux indépendamment de leur position géographique.
Document
1 : Notions et concepts en géographie
| "[...] Une caractéristique qui apparaît toujours dans
la connaissance scientifique et qui ne se retrouve pas, en revanche dans
la connaissance non-scientifique [est] l'explicitation des concepts avec
lesquels la connaissance en question est opérée (Prieto,
1975, p. 150)."
"C'est bien là qu'on peut saisir le drame de la géographie humaine qui a utilisé le processus de conceptualisation car lorsqu'elle a été entraînée vers le haut de la "pyramide conceptuelle" elle a découvert qu'elle se dépouillait de toute spécification et que la réalité à laquelle elle tenait tant lui échappait. La construction des notions par abstractions successives pose donc d'énormes problèmes car au lieu de disposer , au terme de l'effort, de notions rigoureuses et univoques, on se trouve en possession de notions floues, par excès de généralisation, et en conséquence équivoques (p. 59)". "On ne s'est pas vraiment rendu compte que ces notions étaient des constructions à travers lesquelles on construisait en même temps la réalité. [...] Le problème de la réalité s'est surtout posé en géographie lorsqu'on a abandonné les notions exprimées dans le langage naturel au profit des concepts formulés dans le langage logico-mathématique (p.60)" Il y a, en effet, une contradiction dans la géographie classique en ce sens que l'on a accepté le flou, l'équivoque et le schématisme dans les notions mais on ne l'a guère accepté dans les formulations mathématiques. La géographie régionale et celle du paysage a vécu, je crois qu'on peut le dire, avec beaucoup de notions et fort peu de concepts (p.69)". " [...] la plupart, pour ne pas dire tous les concepts logico-mathématiques utilisés ont été créés non pas par une élaboration interne propre à la géographie, mais créés en dehors d'elle. [...] cela signifie que l'on a plaqué sur de vieux problèmes, non résolus par les notions à disposition, de nouveaux concepts sans toujours savoir si ce qu'on faisait était bien cohérent. [...] Est-ce à dire que l'on a trop conceptualisé en géographie humaine ? Evidemment pas ! Je dirais que l'on n'a pas encore conceptualisé mais que l'on a emprunté des concepts. Ce n'est pas la même chose. (p. 71)". " Je crois qu'il est vain, je veux dire par là que cela relève d'un exercice gratuit, de chercher, à tout prix, à quantifier c'est-à-dire à mesurer et à conceptualiser non pas ce qui ne l'est pas mais ce qui ne peut pas encore l'être. (p. 71) "[...] nous devons apprendre à penser les notions géographiques de telle sorte que nous puissions leur donner un contenu logico-mathématique c'est-à-dire aller de la reflexion géographique à la réflexion mathématique et non pas découvrir les mathématiques pour voir ce qu'on peut ensuite en faire en géographie. Tant que les économistes sont allés des mathématiques à l'économie, ils ont mathématisé lleur discipline, quant ils ont fait l'inverse, ils ont créé l'économétrie. Je m'abstiendrais d'imaginer ce que nous ferons mais une chose est en tout cas certaine c'est qu'il y a un risque sérieux de perdre le sens géographique si nous ne prenons pas garde à ce processus. N'est-ce pas déjà une tendance qu'on observe dans la géographie américaine ? " (p. 72). Raffestin C., 1978, "Les construits en géographie humaine : notions et concepts", Géopoint 1978, Univ. de Lyon II, Lausanne et Genève, pp. 55-73 |
Document 2 : Le critère de falsifiabilité de K.R. Popper
Dans le texte ci-dessous, l'épistémologue K.R Popper
cherche à répondre au problème suivant : "quand
doit-on conférer à une théorie un statut scientifique
?" ou encore "existe-t-il un critère permettant d'établir
la nature ou le statut scientifique d'une théorie?"
K.R. Popper, Conjecture et réfutation, Payot, Paris, pp. 58-65. |
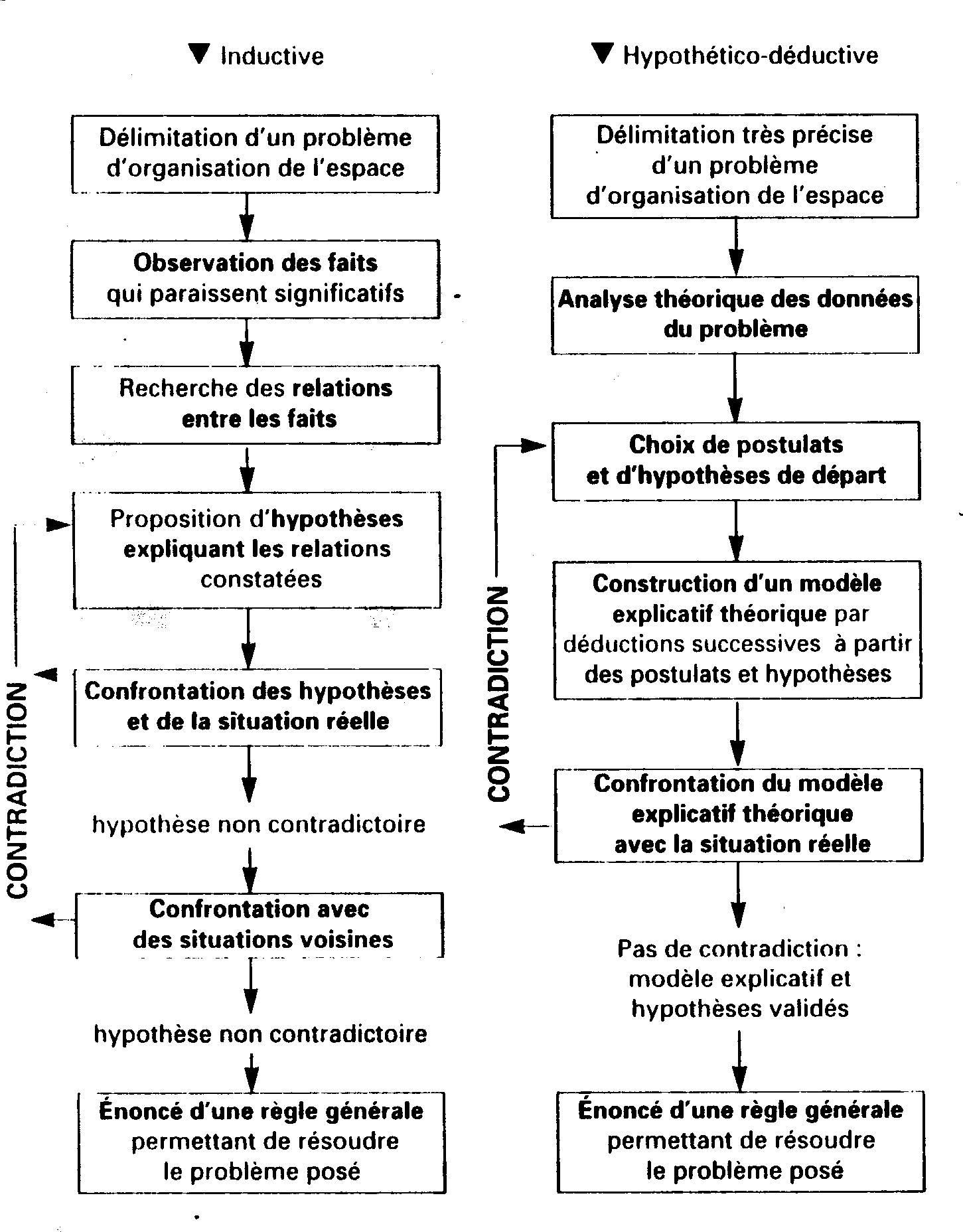
Document 3 : Démarche inductive et démarche hypothético-déductive en géographie

Source : Hugonie G., Géographie-Lycée. Aide à la mise en œuvre des programmes, CNDP/CRDP de Versailles, 1991, p. 15 |
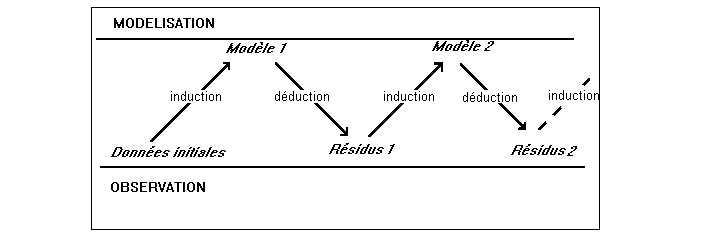
Source : Grasland C., 1995, "Modélisation et commentaire de documents", Feuilles de géographie, n°16.
Document 4 : Les étapes d'une démarche scientifique
Le savoir géographique, comme tout savoir scientifique, se construit à travers une série d'étapes. Ces étapes sont la description, la modélisation, la prévision et l'explication. Au cours de chacune de ces étapes sont mises en oeuvre différentes méthodes qui conditionnent la qualité des résultats obtenus. A travers deux exemples pris en géographie physique et en géographie humaine, nous allons montrer rapidement comment ces étapes s'enchaînent.
(1) La distribution de la taille des villes d'un pays.
(2) La répartition des températures dans
une région montagneuse
| Températures
:
L'analyse des températures à la surface du globe s'est longtemps limité à une appréhension qualitative des lieux : tel lieu fait partie des régions "froides", "tempérées" ou "chaudes" à l'échelle du globe. De même, on a repéré très tôt les étagements de végétation et de température des milieux montagnards Un premier progrès a été le passage du langage littéraire au langage cartographique qui a permis de localiser à la surface du globe les zones froides ou chaudes et de découvrir ainsi le rôle de la latitude et de l'altitude. La mise au point d'outils de mesure précis (thermomètres) a permis une analyse plus précise en utilisant le langage numérique pour quantifier les températures. Des cartes plus précises ont pu être établies en interpolant la situation de stations isolées. Finalement, l'apparition de satellites géostationnaires a permis de mesurer de façon continue l'évolution des températures en tout moment et en tout point du globe, et de les restituer sous forme d'images numériques. |
Taille des villes :
L'analyse de la distribution des tailles de villes est un problème plus complexe que le précédent car le concept de ville ne se laisse pas saisir aussi facilement que celui de température. La variété des définitions de
villes d'un pays à l'autre est éloquente (définitions
morphologiques, fonctionnelles, administratives, ...). Toute étude
de la distribution des villes doit donc partir d'une discussion critique
où l'on définit ce que l'on entend par ville et pourquoi.
La mesure ultérieure de la taille des villes est étroitement
liée aux choix initiaux qui auront été fait.
|
| Température & altitude
:
L'examen de la distribution des températures
en montagne laisse apparaître une diminution de celles-ci vers les
hautes latitudes et en altitudes. Dans le cas des altitudes, on constate
une diminution régulière de -0.6°C tous les 100 mètres.
|
Rang et population des villes :
L'examen de la distribution des tailles de villes montre que celle-ci est fortement dissymétrique : il y a beaucoup de petites villes et peu de petites. Sur un graphique rang-taille on voit se dessiner une courbe hyperbolique. L'examen de plusieurs pays montre l'existence d'une relation du type Pn=P1/n (la taille de la Nième ville est généralement égale à la taille de la plus grande ville divisée par n). |
A certains égards, la modélisation est une description plus synthétique qui permet de résumer un grand nombre d'observations à travers un petit nombre de paramètres. Le modèle n'est jamais parfait, mais il permet de résumer une plus ou moins grande partie du phénomène dans une formule très simple.
| Température :
L'établissement de la relation Tz=-0.6*z+T0 (avec z, altitude en centaine de mètres et T0 altitude au niveau de la mer) me permet par exemple de dire que s'il fait 10°C à Clermont Ferrand (400m d'altitude), alors, il fera un peu moins de 4°C au sommet du Puy de Dôme (1465 m d'altitude). Je n'ai pas besoin de connaître les mécanismes
physiques qui expliquent la diminution des températures en altitudes
puisque je connais la loi empirique.
|
Villes :
Sachant qu'en 1940 la plus grande ville des Etats-Unis, New-York, avait 11690000 habitant, je peux estimer que la 5e ville devait avoir environ P5=P1/5 soit 2338000 habitants. La prévision est bonne puisque Boston, 5e ville à cette époque avait 2351000 h. Il faut toutefois remarquer que l'application à la France serait moins bonne car la loi y est moins bien vérifié : ainsi, on s'attend à ce que la 2ème ville ait 4.5 millions d'habitants alors qu'elle en a à peine plus d'un million. Je ne puis cependant pas qualifier cet écart d'anormal car la loi P1/n n'est pas une "norme" mais une simple régularité observée dans beaucoup de pays. |
Des lois empiriques permettent donc de résumer
des ensembles d'informations à l'aide d'un petit nombre de paramètres
et, dans certains cas, de faire des prévisions en extrapolant
les résultats de ces lois empiriques aux situations pour lesquelles
on ne dispose pas d'information (ou d'une information lacunaire). La prévision
n'impose pas, a priori, la compréhension du phénomène
et de nombreux modèles "stupides" sont utilisés pour prévoir
sans comprendre (ex. cours de la Bourse).
| Température :
La diminution des températures avec l'altitude repose sur des phénomènes physiques clairement identifiables (diminution de la pression atmosphérique avec l'altitude et relation thermodynamique entre pression et température selon la loi PV=NRT). L'explication peut être plus ou moins complexe, elle n'en demeure pas moins unique et peu contestable. Les résidus que l'on peut observer (ex. adret/ubac) témoignent de l'intervention de facteurs secondaires tels que l'exposition, l'ensoleillement, … qui s'ajoutent au phénomène thermodynamique principal.
|
Villes :
Dans le cas des villes, au contraire, plusieurs théories s'affrontent pour rendre compte de l'inégale distribution des tailles. Sans entrer dans leur détail, on soulignera juste qu'il existe beaucoup de phénomènes ou une loi admise par tous fait l'objet d'interprétation divergentes. Le débat théorique ne doit pas être négligé, car il conditionne à certains égards la pratique. Ainsi, le géographe Christaller a voulu régulariser le réseau urbain polonais pendant la deuxième guerre mondiale, car il estimait que la distribution théorique qu'il proposait était la meilleure possible. Cf. aussi le programme de "systématisation" de Ceaucescu en Roumanie. |
Document 5 : La contrainte chorotaxique (H. Reymond)
GOOSE-CITY EN 1846 GOOSE-CITY EN 1851
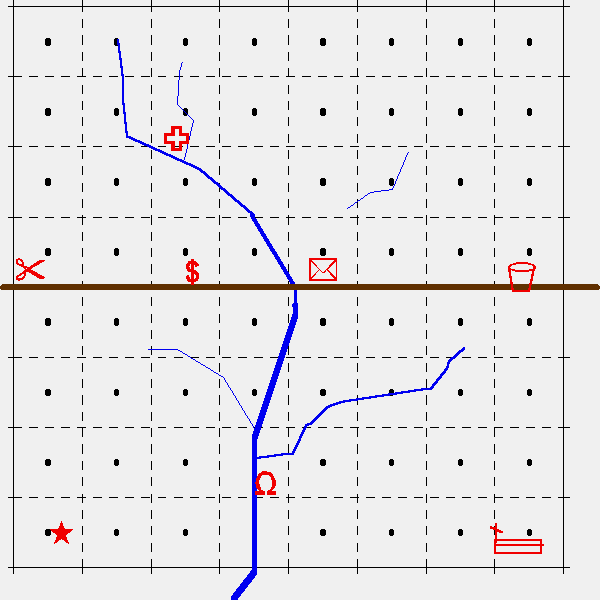
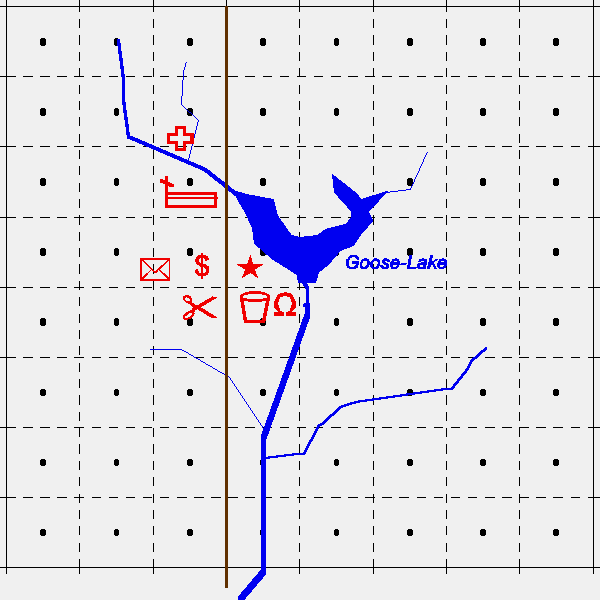

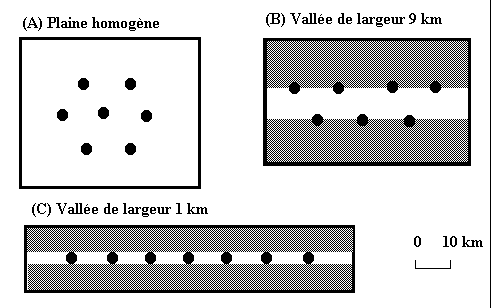
Document 5.b : Comment varient les contraintes spatiales ?
Document 6 : Deux points de vue sur les lois que l'espace impose aux sociétés.
Document 6.a : ROGER BRUNET
| La production de l'espace conserve […]une double détermination,
générale et locale. Tout le problème de la recherche
sur l'espace géographique est de faire le tri entre les lois et
les règles, ce qui vaut à l'échelle mondiale et ce
qui est propre à des modes de production, des cultures ou quoi que
ce soit d'équivalent qui régionalise l'espace - et le temps.
La géographie a d'abord vu le foisonnement de situations uniques,
c'était même sa fonction d'exploratrice. Puis elle a cherché,
à partir de là, à regrouper en types formels ce qui
semblait se ressembler; faute de méthode, ce fut sa période
ingrate. Elle a tendance maintenant à chercher des lois, et à
évaluer des écarts aux lois; c'est aussi pour retrouver l'unique
en l'appréciant mieux. Elle y reprend sel et miel. Ce faisant, elle
a cru pouvoir observer que, non seulement les sociétés ont
leurs lois, au sens strict et au sens large, mais encore l'espace a les
siennes propres. Ces lois sont de nature topologique ou, plus largement,
physique, même s'agissant de phénomènes sociaux. Leur
découverte a donné lieu à une abondante littérature,
et à d'infinis raffinements techniques. Au point qu'elles n'ont
pas échappé aux phénomènes classiques d'aliénation
et de réification, certains chercheurs s'acharnant autour des équations
en perdant de vue toute relation avec les processus réels. Comme
l'espace lui-même, les lois de l'espace n'ont de réalité
que dans la mesure où elles expriment des relations sociales, où
elles ont une logique sociale. Elles concernant des populations concrètes,
leurs échanges et leurs œuvres. La géographie se déploie
ici entre deux aliénations: chercher des lois sans s'interroger
sur les pratiques qu'elles recouvrent, des lois comme immanentes ou célestes;
ou nier toute loi de l'espace parce qu'il n'y aurait de loi que de la société,
ou même de l'économie, voire du politique, non moins réifiées
à leur tour. Mais on ne fait pas ce que l'on veut de et dans l'espace.
Densité, distance, diffusion et quelques autres phénomènes
sont spécifiquement phénomènes de l'espace. Bien entendu,
quand ils concernant l'espace géographique tout entier, et pas seulement
le relief ou la couverture végétale, ils n'existent qu'à
travers les relations sociales; ils n'en ont pas moins leurs lois et leurs
effets propres, dont les sociétés ont le plus grand intérêt
à tenir compte. Il est assez d'échecs d'implantation pour
le rappeler.
Source : R. Brunet, Mondes Nouveaux / Géographie Universelle tome I, Hachette-Reclus, 1990, p. 79 |
Document 6.b JACQUES LEVY
| Axiome 1 : L'espace est une catégorie correspondant,
selon la tradition marxiste, à un mode d'existence de la matière.
La spatialité ne peut être définie en soi, indépendamment
du "contenu" de réel qui l'organise.
Axiome 2 : L'espace social, c'est-à-dire la répartition des phénomènes sociaux selon les deux dimensions courbes de la surface terrestre ne pose pas forcément un problème intéressant à la société. Si les localisations sont rendues quasi impératives par l'absence de maîtrise des hommes sur leurs conditions de vie, on est en présence d'une société pré-spatiale ; si, à l'inverse, la liberté d'allouer des éléments de la société ici ou là est totale, si l'ubiquité matérielle (transports) ou immatérielle (télécommunications) génère une totale isotropie, on peut dire que la société est de nature post-spatiale. On posera donc que c'est dans la phase transitoire entre ces deux situations extrêmes que prend sens une approche scientifique de l'espace social. Axiome 3 : Une fois rejeté le primat de l'économique, du sociologique ou du politique dans l'explication des faits sociaux (on ne peut comprendre les rapports marchands sans se référer aux rapports sociaux, ni ces derniers sans reconnaître l'existence d'un pouvoir politique), force est de reconnaître qu'il ne peut y avoir de hiérarchie entre les sciences sociales dès lors que chacune d'entre elle est capable de prendre en compte l'ensemble du réel social, la généralité des phénomènes qui constituent une société. Axiome 4 : Il n'est pas possible d'isoler un ensemble de "choses" de la société telles que nous puissions comprendre leur fonctionnement sans faire entrer le reste de la société dans notre raisonnement. Toutes les sciences sociales sont donc à la fois totales et partielles ; elles représentent une dimension qui est aussi un problème - une liberté et des contraintes, des choix et un enjeu - pour la société qui pousse certains de ses membres à y réfléchir. Source : J. Lévy, "L’espace et le politique : quelles rencontres ? " in Brunet R., Auriac F., 1986, Espaces, jeux et enjeux, Fayard-Diderot, Paris, pp. 251-268 |
Document 7 : Analyse statistique des phénomènes géographiques
Matrice d’information géographique : ce terme inventé par le géographe américain B. Berry décrit un tableau à trois dimensions (cube) dans lequel les lignes (i) correspondent aux unités géographiques, les colonnes (j) correspondent aux caractères permettant de décrire ces unités géographiques, les plans étagés (t) correspondent aux dates ou périodes pour lesquelles ces attributs ont été mesurés.Un élément quelconque d’une matrice d’information géographique se note Xijtet désigne la " situation du lieu i, pour le caractère j au temps t ".
|
1980
|
Pop | Sup | Den | ||
|
1990
|
Pop | Sup | Den |
5
|
|
|
2000
|
Pop | Sup | Den |
10
|
16
|
| A |
1000
|
67
|
15
|
17
|
30
|
| B |
5000
|
19
|
19
|
31
|
8
|
| C |
2000
|
23
|
32
|
10
|
|
| D |
1000
|
46
|
23
|
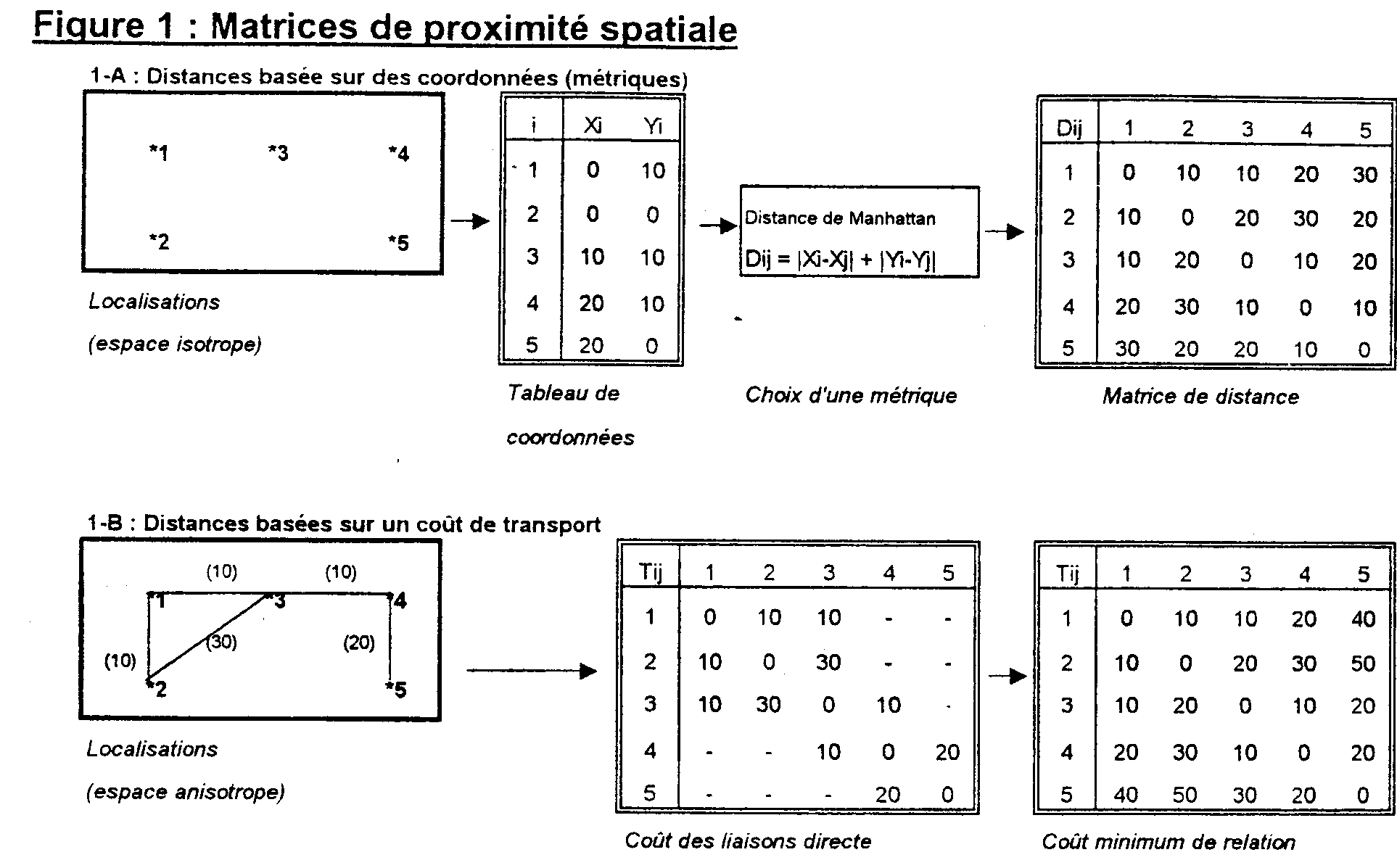
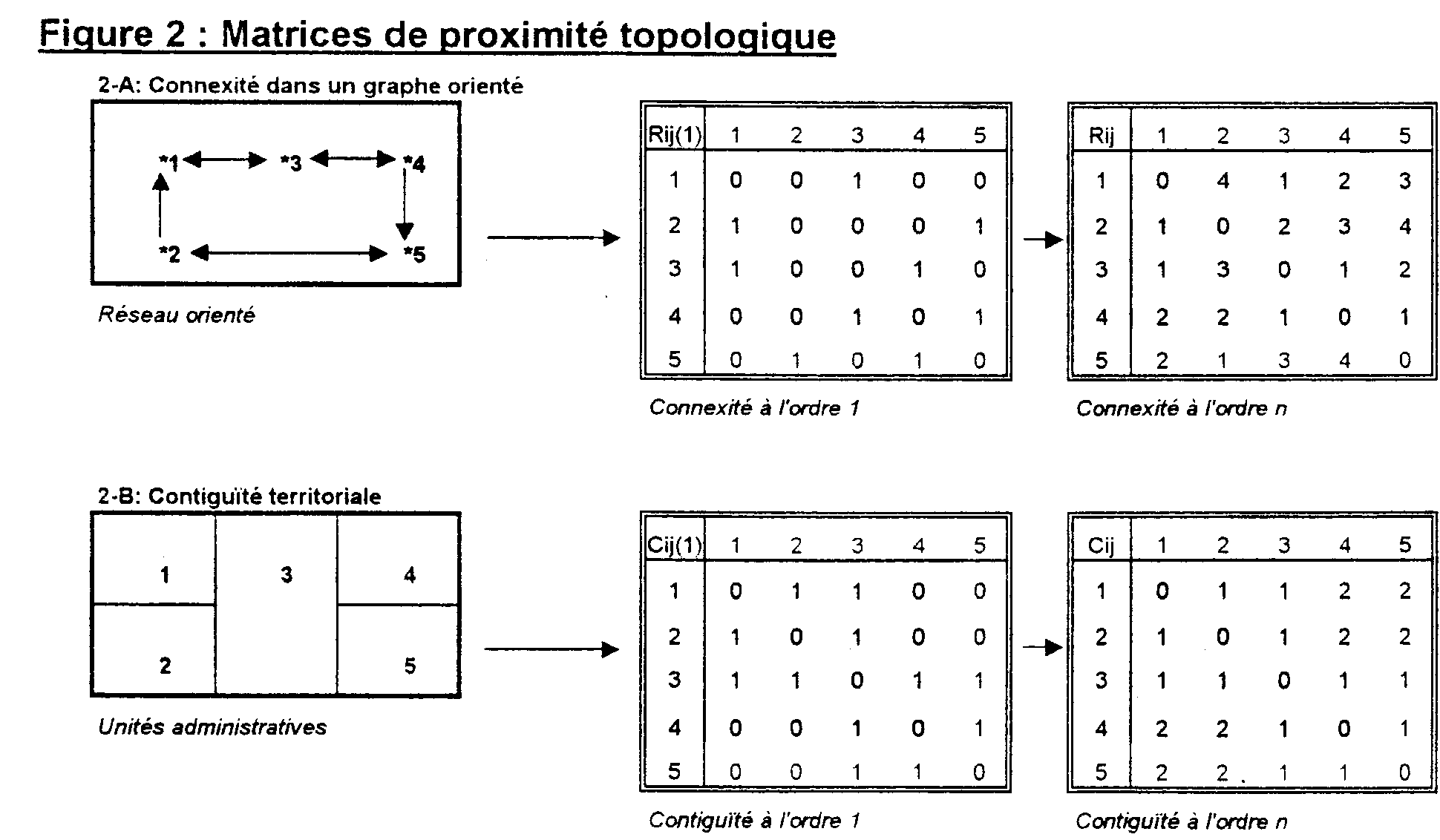
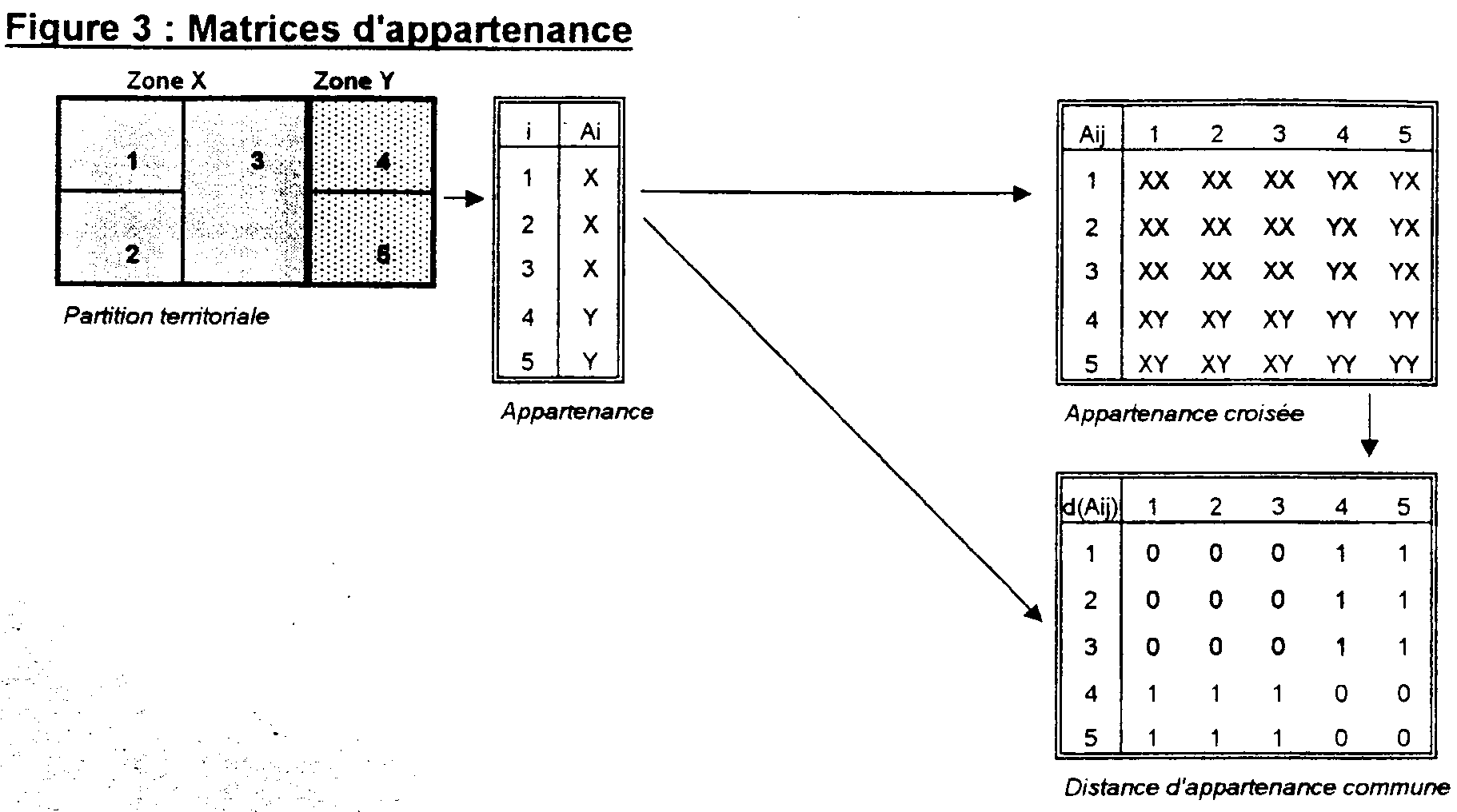
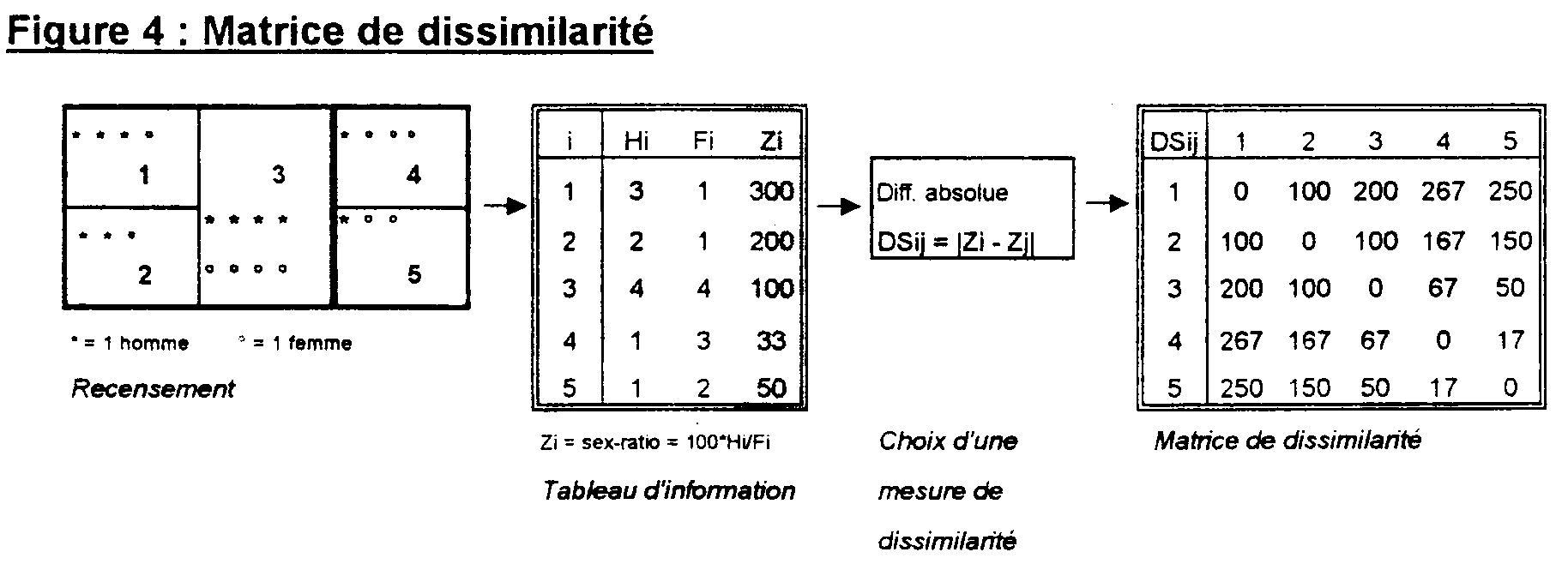
Matrice de relation spatiale : une matrice de relation spatiale correspond à un tableau ou les lignes et les colonnes correspondent à des lieux. A chaque couple de lieu (i,j) est associée une information décrivant un type de relations entre les lieux considérés.Une troisième dimension (t) correspond à l'évolution de ces relations au cours du temps. On peut distinguer plusieurs grandes familles de relations. Une typologie possible distingue 4 familles :
Document
9 : Types de matrices de relations entre lieux