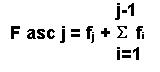Distribution statistique: pour un caractère
quantitatif, ensemble ordonné des modalités prises par le
caractère X par l'ensemble des éléments de E. Le
tableau de distribution statistique est un tableau élémentaire
dans lequel les valeurs du caractère X ont été ordonnées.
A chaque modalité Xi de ce tableau on peut donc associer un rang
qui est sa position dans le classement des valeurs de la plus petite.
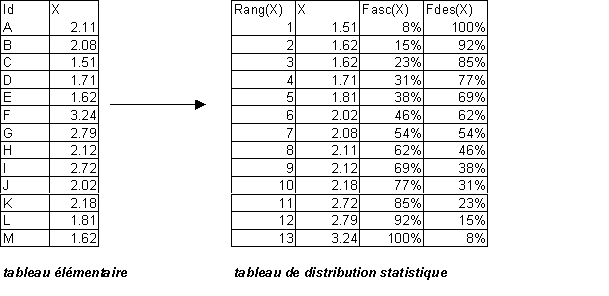
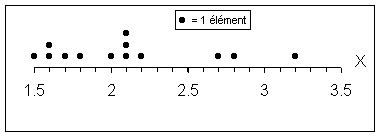
Diagramme de distribution : représentation
élémentaire et unidimensionnelle d’une distribution statistique,
consistant à représenter chaque élément de
la distribution par un point sur un axe gradué. Lorsque deux éléments
ont des modalités identiques ou très proche, on procède
à un " empilement " des points. Le diagramme de distribution correspond
alors à un histogramme utilisant de très petites classes
d’effectifs égaux.
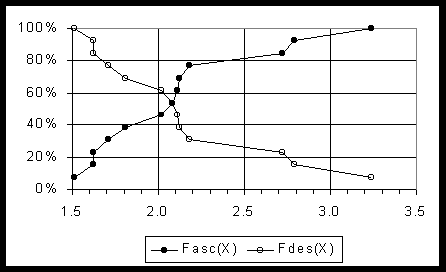
Courbes des fréquences cumulées (1)
: La construction élémentaire de la courbe des fréquences
cumulées consiste à associer à chaque modalité
du tableau de distribution statistique sa fréquence cumulée
ascendante
(% des éléments ayant des modalités de valeur inférieure
ou égale) et sa fréquence cumulée
descendante (%
des éléments ayant des modalités de valeur supérieure
ou égale)
F asc i = Ri / N
F des i = 1 – (Ri/N)
On représente alors sur le graphique le croisement
des modalités Xi (en abscisse) avec leur fréquence cumulée
ascendante ou descendante (en ordonnée).
- Zones de concentration- Zones de dispersion – discontinuités
: Diagramme de distribution et courbes des fréquences cumulées
permettent de repérer les zones de concentration de la distribution
(beaucoup
d’éléments sur un intervalle) et les zones de dispersion
(peu d’éléments sur un intervalle). On peut également
repérer des discontinuités, c’est-à-dire des
zones de dispersion séparant deux zones de concentration des éléments.
Sur la courbe des fréquences cumulées :
Les pentes fortes correspondent aux zones de concentration
des valeurs
Les pentes faibles correspondent aux zones de dispersion
des valeurs
Les " marches d’escalier " correspondent aux discontinuités
de la distribution
1- Les classes correspondent à une partition
de l'ensemble de l'intervalle de variation du caractère. (intervalle
allant de la valeur minimum prise par X dans l'ensemble étudié,
à la valeur minimum prise par X dans l'ensemble étudié).
Ces classes doivent être disjointes (l'intersection de deux classes
est nulle, un élément ne peut appartenir qu'à une
seule classe), et continues (la partition doit être exhaustive, elle
doit intégrer toutes les valeurs que pourrait prendre le caractère
dans l'intervalle de variation considéré. Chacune des k classes,
j étant une classe quelconque, est définie par une borne
inférieure Binf j et une borne supérieure, nj est le nombre
d'éléments compris dans l'intervalle [Binf j ; Bsup j[
2- l'effectif des classes nj est le nombre d'individus appartenant
à chaque classe j.
3- La fréquence simple des classes
:
fi = nj / N
4- L'amplitude des classe :
Aj = Bsup j -Binf j
5- Le centre de la classe :
Cj = [ Bsup j + Binf j ] / 2
6- La fréquence moyenne ou densité
d'effectif :
fmj = fj / Aj
7- La fréquence cumulée ascendante
de la classe j est la proportion d'éléments qui pour le caractère
X enregistrent une valeur inférieure à celle de sa
borne supérieure.
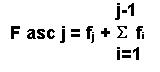
8- La fréquence cumulée descendante de
la classe j est la proportion d'éléments qui, pour le caractère
X enregistrent une valeur supérieure à celle de sa
borne inférieure
Fdesj = 1- Fascj
Elles sont au nombre de deux pour les caractères
continus :
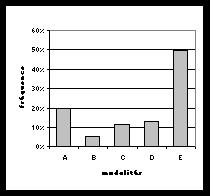
1- L'histogramme est établi à partir
d'un tableau de dénombrement. C'est une représentation bi-dimensionnelle
qui présente chaque classe sous la forme d'une rectangle dont la
base est proportionnelle à l'amplitude de la classe et la
hauteur à la fréquence moyenne de la classe. La surface
du rectangle est donc proportionnelle à l'effectif de la classe
(ou la fréquence simple de la classe) puisque :
Surface du rectangle = ( longueur x largeur) = ( fmj
x
Aj) = (fj / Aj) x Aj = fj
La légende d'un histogramme est constituée
par un élément de surface dont on indique la part des éléments
qu'il représente (exprimée en fréquence simple ou
en effectif).
L' histogramme permet une double lecture de la distribution
statistique:
1) La hauteur du rectangle (ordonnée) renseigne
sur la densité des éléments dans chaque classe. Une
forte fréquence moyenne indique une concentration des valeurs, une
faible fréquence moyenne indique une dispersion des valeurs.
2) La surface des rectangles renseigne sur l'effectif
de chaque classe.
2- Les courbe des fréquences cumulées
ascendantes et descendantes sont établies à partir du tableau
de distribution statistique ou à partir d'un tableau de dénombrement.
C'est un graphique bi-dimensionnel représentant en abscisse les
modalités du caractère X et en ordonnée, les fréquences
cumulées . Sa construction est la suivante :
- La fréquence cumulée ascendante
On porte en abscisse les valeurs correspondant aux bornes des classes de
la partition du caractère X et en ordonnée les fréquences
cumulées ascendantes correspondantes. On repère les points
correspondant à ces couples de valeurs auxquels on ajoute le point
qui a pour abscisse la borne inférieure de la première classe,
qui correspond à X min, et pour ordonnée 0 (en effet, 0 ou
0% des éléments enregistrent des valeurs inférieures
à X min). On procède à une extrapolation linéaire
entre ces points (hypothèse d'équirépartition des
éléments dans chaque classe), en reliant ces points par une
droite.
- La fréquence cumulée descendante On
procède de la même manière mais en sens inverse. Les
valeurs de fréquence cumulée descendantes sont égales
à (100% - valeur de la fréquence cumulées ascendante)
Les courbes obtenues se croisent au point de fréquence
cumulée ascendante ou descendante 0.5 ou 50%. La valeur du caractère
X correspondant à cette fréquence cumulée 0.5 ou 50%
et que l'on peut directement lire sur le graphique en ordonnée est
la médiane (50 % des éléments sont supérieurs
à cette valeur de X et 50 % lui sont inférieurs). On notera
ce point X méd