PLAN DU CHAPITRE STAT.5

INTRODUCTION :

1. LA DISCRETISATION

1.1 Dichotomie (2 modalités)

• Choix de la valeur de référence
• Transformation
• Mise en relation

• Amplitudes égales
• Effectifs égaux (quantiles)
• Utilisation de la moyenne et de l'écart-type

2. LA TRANSFORMATION EN RANGS

2.1 Définition des rangs en statistique

• Ordre ascendant ou descendant
• Problème des ex-aequo

• Elimination des valeurs exceptionnelles
• Elimination des zones de concentration et de dispersion

3. LA TRANSFORMATION EN INDICE

3.1 Indices fondés sur une valeur centrale

• Choix de la valeur de référence
• Exemple d'utilisation : les séries chronologiques

• Choix de l'intervalle de référence
• Exemples d'utilisation : l'IDH

4. LA STANDARDISATION

4.1 Centrage et réduction

• Centrage par rapport à la moyenne
• Réduction par rapport à l'écart-type

• Moyenne=0 / écart-type = 1
• Signification probabiliste.

5. UNE APPLICATION : LA MATRICE BERTIN

5.1 Du tableau élémentaire au tableau standardisé

5.2 Regroupement des colonnes (étude des corrélations)

5.3 Regroupement des lignes (classification)

VOCABULAIRE DU CHAPITRE STAT.5

La comparaison de plusieurs caractères quantitatifs ou bien celle de caractères quantitatifs et qualitatifs, n'est généralement pas possible à partir du tableau élémentaire car les caractères à comparer peuvent avoir :

- des unités de mesure différentes.

- des ordres de grandeur différents (valeurs centrales)

- des dispersions différentes (paramètres de dispersion).

- des modalités qualitatives

Tableau 1 : Indicateurs de santé de 9 pays développés en 1995
 

Pays	% fumeurs	% fumeurs	cons. Alcool	cas de Sida
	homme	femmes	(litres/hab.)	p. 100 000 h.
	1986-95	1986-95	1995	1995
	(V1)	(V2)	(V3)	(V4)
Canada	31	29	6.1	2.7
France	40	27	11.9	6.3
Norvège	26	36	3.9	1.0
Etats-Unis	28	23	6.6	13.8
Finlande	27	19	6.4	0.4
Pays-Bas	36	29	7.9	2.4
Japon	59	15	6.8	0.2
Nouvelle-Zélande	24	22	7.2	1.6
Suède	22	24	5.7	1.5
Moyenne	32.6	24.9	6.9	3.3
écart-type	10.8	5.8	2.0	4.1
Min	22	15	3.9	0.2
Médiane	28	24	6.6	1.6
max	59	36	11.9	13.8

Source : Rapport sur le développement humain, 1998, p. 210

=> Dans le tableau 1, il est difficile de comparer les valeurs des différentes colonnes car elles ont des ordres de grandeur différent (V1 et V2) ou des unités de mesure différentes (V2,V3,V4).
 
 

Il est donc généralement nécessaire de transformer les caractères quantitatifs à étudier avant de pouvoir les comparer les uns aux autres. Quatre types de transformations sont présentées.
 
 

1) La discrétisation,

La discrétisation consiste à transformer un caractère quantitatif continu en caractère discret. On parle de dichotomie lorsque le caractère discret n'a que deux modalités.

* dichotomie (2 modalités)

On fixe un seuil X_ref qui définit la limite entre les valeurs fortes et faibles de X_i. X_ref peut être une valeur centrale (moyenne, médiane) ou bien une valeur qui possède une signification particulière pour l'interprétation. On crée la variable qualitative X' ayant deux modalités (+ ou - ) selon procédure suivante :

X'_i = + si X _i est supérieur à X_ref

X' _i = - si X _i est inférieur ou égal à X_ref
 
 

Tableau 2 : Discrétisation en 2 classes fondées sur la médiane
 

Pays	(V1)	(V2)	(V3)	(V4)	nb. de +
Canada	+	+	-	+	3
France	+	+	+	+	4
Norvège	-	+	-	-	1
Etats-Unis	-	-	-	+	1
Finlande	-	-	-	-	0
Pays-Bas	+	+	+	+	4
Japon	+	-	+	-	2
Nouvelle-Zélande	-	-	+	-	1
Suède	-	-	-	-	0

=> On repère immédiatement les pays situés au dessus ou au dessous de la médiane pour chacun des critères. On peut également dénombrer le nombre de valeurs + ou - si les indicateurs sont de même nature (ici, des pathologies). On remarque que le Canada et la France ont des valeurs élevées pour 4 pathologies alors que la Suède et la Finlande ont régulièrement des valeurs faibles.

* autres méthodes de discrétisation :

On n'est évidemment pas obligé de se limiter à deux classes et l'on peut construire des discrétisations en 3, 4, 5 classes ou plus, en utilisant les méthodes de partition qui ont été apprises dans les chapitres précédents (effectifs égaux, amplitudes égales, utilisation de la moyenne et de l'écart-type, etc.). La seule règle à respecter est d'utiliser la même méthode de discrétisation pour tous les caractères du tableau, faute de quoi les comparaisons ne seraient pas valables.

2) La transformation en rangs

Chaque modalité du caractère X _i est transformée en une modalité d'un caractère qualitatif ordinal X' _i qui indique le rang pris par l'élément Xi dans la série X₁..X_n (n étant le nombre d'éléments de l'ensemble observé).

X'_i => rang de X _i dans la distribution statistique de X

La méthode ne pose pas de problème mais il faut faire attention à deux choses :

1) l'ordre de classement (croissant ou décroissant) doit être spécifié et être a priori le même pour les différents caractères que l'on veut comparer

2) lorsqu'il y a des ex-aequo, on leur attribue comme rang la moyenne des places qu'ils auraient occupées s'ils avaient été à la suite les uns des autres. On reprend ensuite le classement après les rangs virtuellement occupés. Si les rangs sont correctement construits, leur somme doit être égale à n(n+1)/2 .

La méthode des rangs donne de bons résultats mais il faut être conscient du fait que

1. Elle accroît les écarts dans les zones de concentration de la distribution
2. Elle réduit les écarts dans les zones de dispersion et élimine toute les discontinuités qui peuvent exister entre les valeurs (Cf. exemple)

• On remarquera que pour la variable V2, la France et le Canada sont ex-aequo à la deuxième place. On leur attribue donc la moyenne des rangs 2 et 3, soit la valeur 2.5.
• Dans le cas du SIDA (V4) il y a un gros écart entre la France (6.3) et les Etats-Unis (11.8) qui ne sont pourtant séparés que par un seul rang de différence. Il y a en revanche peu d'écarts entre la Norvège (1.0) et les Pays-Bas (2.4) qui sont pourtant séparés par 3 rangs.
• La moyenne des rangs permet de définir un indicateur de position globale sur l'ensemble des critères. : La France (2.3) et les Pays-Bas (2.9) sont lanterne rouge alors que la Suède et la Finlande (7.0) affichent la meilleure situation sanitaire.

Lorsque l'on veut comparer deux caractères quantitatifs ayant des ordres de grandeur ou des unités de mesure différentes, on peut les transformer en indices. Il existe deux méthodes, selon que l'on construit l'indice par rapport à une valeur de référence ou par rapport à un intervalle.

* Indices fondés sur une valeur de référence

1. On choisit une valeur de référence X_ref pour la distribution de X
2. On choisit une base B de l'indice (généralement 1 ou 100)

X'_i = B. X_i / X_ref

Le cas le plus fréquent est de choisir une valeur centrale comme base de l'indice ("indice 100 = moyenne" ou "indice 100 = médiane"). Dans le cas particulier des séries chronologiques (X1 . Xt désigne la valeur de X à différentes dates 1.t) on choisit souvent une année particulière (début, fin, milieu de la période, .) comme référence et on précise alors "Indice 100 = valeur de X au temps t".

Tableau 4 : transformation en indices 100 = moyenne
 

Pays	(V1)	(V2)	(V3)	(V4)	moyenne
Canada	95	117	88	81	95
France	123	108	171	190	148
Norvège	80	145	56	30	78
Etats-Unis	86	92	95	415	172
Finlande	83	76	92	12	66
Pays-Bas	111	117	114	72	103
Japon	181	60	98	6	86
Nouvelle-Zélande	74	88	104	48	78
Suède	68	96	82	45	73
Moyenne	100	100	100	100	100

* Indices fondés sur un intervalle de référence

On peut également utiliser une standardisation fondée sur l'emploi d'un intervalle de référence comprenant une valeur minimale (X_min) et une valeur maximale (X_max) Ces valeurs maximales et minimales peuvent être soit celles de la distribution proprement dite, soit celles du phénomène étudié (l'intervalle est dans ce cas plus large que les valeurs réellement observées de la distribution).

L'opération consiste à mesurer la position des valeurs X_i sur l'intervalle défini par les maximales et minimales, de manière à aboutir à une nouvelle variable X'_i strictement comprise entre 0 (minimum) et 1 (maximum) :

X'_i = (X_i - X_min) / (X_max - X_min)

Cette méthode est notamment utilisée par les Nations Unies pour définir l'indicateur de développement humain (IDH) qui exprime le degré de satisfaction des besoins essentiels (longévité, scolarisation, revenus) sur des échelles comprises entre 0 (pays les plus pauvres) et 1 (pays où les besoins minimums sont pleinement satisfaits).

Tableau 5 : transformation en indices fondées sur le minimum et le maximum

Pays	(V1)	(V2)	(V3)	(V4)	Moyenne
Canada	0.243	0.667	0.275	0.184	0.342
France	0.486	0.571	1.000	0.449	0.627
Norvège	0.108	1.000	0.000	0.059	0.292
Etats-Unis	0.162	0.381	0.338	1.000	0.470
Finlande	0.135	0.190	0.313	0.015	0.163
Pays-Bas	0.378	0.667	0.500	0.162	0.427
Japon	1.000	0.000	0.363	0.000	0.341
Nouvelle-Zélande	0.054	0.333	0.413	0.103	0.226
Suède	0.000	0.429	0.225	0.096	0.187

=> On a utilisé ici les valeurs minimum et maximum de la distribution des 9 pays comme référence. On aurait pu également utiliser les valeurs minimum et maximum à l'échelle de l'ensemble de la planète. En tout état de cause, la situation de la France demeure peu glorieuse à l'intérieur de l'échantillon de pays considéré.
 
 

4) La standardisation
 

La standardisation est sans doute la transformation la plus efficace quand on veut comparer deux variables quantitatives. Elle consiste à opérer une double transformation de centrage et de réduction.

Centrage : L'opération de centrage consiste à transformer un caractère X en un caractère X' qui exprime les écarts positifs ou négatifs par rapport à une valeur de référence qui est la moyenne arithmétique de la distribution
 

X' _i = X _i / s(X)

Dans la plupart des cas, on utilise l'écart-type pour effectuer la réduction.

Standardisation : une variable standardisée (on dit aussi centrée-réduite) a été centrée par la moyenne et réduite par l'écart-type :
 

X' _i = (X _i - moyenne de X)/s(X)

Une variable standardisée (centrée-réduite) possède une moyenne de 0 et un écart type de 1. Elle exprime l'écart d'un élément de la distribution à la moyenne, mesuré en écarts-types. L'unité de mesure de la variable d'origine a donc disparu et il est toujours possible de comparer deux variables standardisées.

L'interprétation des valeurs standardisées se fait par rapport au référentiel constitué par la courbe de Gauss (loi Normale) qui a été présentée dans le chapitre précédent (STAT.4). Compte tenu des probabilités associées aux déviations par rapport à la moyenne mesurées en écart-type, on peut proposer une grille d'interprétation qualitative des valeurs standardisées :
 

valeur standardisée	signification qualitative
-3 <	exceptionnellement faible
-3 à -2	très faible
-2 à -1	faible
-1 à 0	assez  faible
0 à +1	assez fort
+1 à +2	fort
+2 à +3	très fort
>  +3	exceptionnellement fort

Un tableau de valeur standardisées permet de repérer très facilement les valeurs exceptionnelles (inférieures à -2 ou supérieures à +2). Avec un peu d'habitude, il permet également de commenter très rapidement la position de chaque élément par rapport à un grand nombre de caractères.
 

Pays	(V1)	(V2)	(V3)	(V4)	moyenne
Canada	-0.14	0.70	-0.41	-0.15	0.00
France	0.69	0.36	2.43	0.73	1.05
Norvège	-0.61	1.90	-1.49	-0.57	-0.19
Etats-Unis	-0.42	-0.32	-0.17	2.57	0.41
Finlande	-0.51	-1.01	-0.27	-0.72	-0.63
Pays-Bas	0.32	0.70	0.47	-0.23	0.32
Japon	2.45	-1.69	-0.07	-0.77	-0.02
Nouvelle-Zélande	-0.79	-0.49	0.13	-0.42	-0.40
Suède	-0.98	-0.15	-0.61	-0.45	-0.55
moyenne	0.00	0.00	0.00	0.00	0.00
écart-type	1.00	1.00	1.00	1.00	1.00

• Une lecture rapide du tableau permet de repérer trois valeurs exceptionnelles : le fort tabagisme masculin au Japon (+2.45), le fort alcoolisme français (+2.43) et l'importance de l'épidémie de SIDA aux Etats-Unis (+2.57). En sens inverse, on notera le faible tabagisme des femmes japonaises (-1.69) et la tempérance des norvégiens face à l'alcool (-1.49) .
• Le profil d'un pays peut-être saisi très rapidement (examen des plus fortes déviations positives et négatives) et l'on peut opérer une synthèse en effectuant la moyenne des valeurs standardisées. On repère ainsi le caractère "moyen'" de la situation du Canada (0.0), la situation privilégiée de la Finlande (-0.63) et . la mauvaise situation sanitaire globale de la France (+1.05). Il convient toutefois de préciser que les conclusions dépendent du référentiel adopté (les 9 pays retenus dans l'étude).

5) Une application : la matrice BERTIN

Mises au point à l'époque où les méthodes statistiques étaient encore peu employées en sciences sociales et où les ordinateurs étaient difficiles d'accès, les méthodes de traitement graphique de l'information mises au point par Jacques Bertin ont été en parties supplantées par d'autres outils (analyse factorielle, classification automatique, ...). Elles demeurent cependant encore très utiles pour apprendre la statisique bivariée ou multivariée et pour présenter les résultats d'une analyse statistique. On se limitera ici à la présentation de la méthode d'analyse de la « Matrice Bertin » qui consiste à transformer un tableau numérique en tableau graphique pour ensuite examiner les relations entre les lignes et les relations entre les colonnes. Pour plus de détails, voir :

• Bertin J., 1977, La graphique et le traitement graphique de l'information, Paris, Flammarion
• Bonin S., 1975, Initiation à la graphique, Paris, Epi. Editeur.

A titre d'exemple, nous allons étudier un tableau relatif à la situation démographique en 1999 des 15 pays issus de l'Union Soviétique.

Liste des variables :

JEU = part des 0-14 ans dans la population totale (en % de la pop. Totale)

VIE = part des + de 60 ans dans la population totale (en % de la pop. Totale)

TMI  = taux de mortalité infantile (en décés de 0-1 an p. 1000 naissances)

DEN = Densité de population (en hab./km2)

URB = Taux d'urbanisation (en % de la pop. Totale)

ISF = Indice synthétique de fécondité (en nombre d'enfants par femme)

1ere étape : passage du tableau brut au tableau standardisé

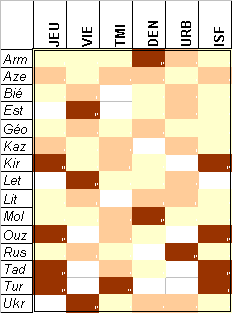
2e étape : passage du tableau standardisé au tableau graphique

On remplace les valeurs standardisées fortes et faibles par des trames allant du clair au foncé. Ici, on a utilisé les seuils min, moy-1 ect, moy, moy + 1 ect., max pour définir les quatre classes visuelles.

3e étape : Regroupement des colonnes

On réordonne les colonnes de la matrice pour rapprocher les colonnes qui se ressemblent et séparer celles qui sont différentes. On repère ainsi des corrélations positives (ex. JEU & TMI ou URB & VIE), des corrélations négatives (ex. TMI & URB) et des absences de corrélation (ex. VIE & DEN).

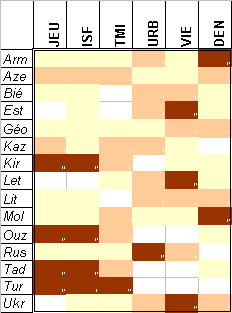
4e étape : Regroupement des lignes

On réordonne les lignes de la matrice pour rapprocher les individus qui se ressemblent et séparer ceux qui sont différentes. On repère ainsi des groupes d'individus ressemblants (ex. Tur-Ouz-Tad-Kir ) ou absolument opposés (Tur & Ukr)

5e étape : Synthèse des résultats

On peut cartographier les résultats de la typologie puis fournir une interprétation générale du tableau en combinant l'étude des lignes et des colonnes.

EXEMPLES DU CHAPITRE STAT.5