Chapitre 5 : TRANSFORMATION ET COMPARAISON DE CARACTERES QUANTITATIFS
INTRODUCTION
5.1 DISCRETISATION
5.2 TRANSFORMATION EN RANGS
5.3 TRANSFORMATION EN INDICE
5.4 STANDARDISATION
CONCLUSION
|
|
|
|
INTRODUCTION
L'étude d'un ensemble d'individus se fait généralement
à travers la prise en compte simultanée de plusieurs indicateurs.
En se limitant au cas où ces caractères sont quantitatifs,
nous allons examiner comment il est possible d'évaluer simultanément
la position d'un individu sur plusieurs distributions. Par exemple,
le même indicateur à différentes dates ou des indicateurs
différents à une même date.
Le problème est que la comparaison des valeurs de deux indicateurs pour un même individu n'est généralement pas possible à partir du tableau brut car les caractères à comparer peuvent avoir :
- des unités de mesure différentes.
- des ordres de grandeur différents (valeurs centrales)
- des dispersions différentes (paramètres de dispersion).
Il est donc généralement nécéssaire de transformer
les caractères à étudier avant de pouvoir les comparer
les uns aux autres.
Pour illustrer le problème, on se limitera à un exemple simple qui est la comparaison de deux caractères décrivant 25 villes françaises au début des années 1990 en fonction des variables suivantes :
X : population de l'agglomération urbaine au recensement de 1990
Y : nombre de fautes d'orthographes commises par les quatre meilleurs
candidats de la ville au concours des "Dicos d'Or" organisé par
B. Pivot sur France 3 en 1993. Les données correspondantes sont
présentées dans le tableau 1 ci dessous.
Tableau
1 : Population de 25 villes françaises en 1990 et résultats
au concours d'orthographe de France 3 en 1993
| Ville | Code | Popul. (X) | Fautes (Y) |
| Besançon | Bn |
121
|
18
|
| Bordeaux | Bo |
640
|
8
|
| Beauvais | Bs |
51
|
13.5
|
| Caen | Ca |
184
|
14
|
| Clermont-Ferrand | Cl |
256
|
8.5
|
| Dijon | Di |
216
|
11
|
| Fort-de-France | Fo |
100
|
33
|
| Lannion | La |
15
|
9.5
|
| Le Mans | Le |
191
|
10
|
| Lille | Li |
936
|
9.5
|
| Limoges | Lm |
172
|
21.5
|
| Lyon | Ly |
1221
|
9.5
|
| Marseille | Ma |
1111
|
9
|
| Montpellier | Mo |
221
|
16
|
| Meaux | Mx |
56
|
8
|
| Metz | Mz |
186
|
11
|
| Nantes | Na |
465
|
9.5
|
| Nice | Ni |
449
|
9
|
| Orléans | Or |
220
|
12.5
|
| Paris | Pa |
8707
|
8
|
| Poitiers | Po |
103
|
19.5
|
| Reims | Re |
199
|
9.5
|
| Rouen | Ro |
380
|
12.5
|
| Strasbourg | St |
373
|
8
|
| Toulouse | To |
541
|
7
|
On a par ailleurs calculé les paramètres principaux de chacune des deux distributions (Tableau 2)
Tableau 2 : paramètres principaux des deux distributions
| Popul. | Fautes | |
| Moyenne |
685
|
12.2
|
| écart-type |
1668
|
5.7
|
| Q1 |
172
|
9
|
| Médiane |
220
|
9.5
|
| Q3 |
465
|
13.5
|
La question soulevée par le tableau 1 est la suivante : "Existe-t-il une relation entre la taille des villes et leur succès au concours d'orthographe de France 3" ou, si l'on préfère, "les champions représentant des petites agglomérations ont-ils commis en moyenne plus (ou moins) de fautes que ceux des grandes agglomérations ?"
L'examen des lignes du tableau
1 ne permet pas d'apporter une réponse aisée à
cette question car les ordres de grandeur et la dispersion des variables
X et Y sont différents et il faut sans cesse se reporter au
tableau
2 pour déterminer si les valeurs de X et de Y peuvent être
considérer comme fortes, moyennes ou faible, par référence
au reste de la distribution des villes. Il est donc nécessaire de
trouver une solution plus pratique pour effectuer ces comparaisons et pour
examiner la position de chaque ville.
5.1 DISCRETISATION
La solution la plus simple, mais aussi la plus brutale consiste à discrétiser les deux variables quantitatives X et Y c'est-à-dire à les ramener à des modalités qualitatives qui pourront être ensuite facilement comparées entre elles.La méthode dichotomique (discrétisation en deux classes)
La discrétisation en deux classes (dichotomie) consiste
à fixer une valeur de référence pour chaque
distribution puis à attribuer à chaque individu une
modalité '+' ou '-' selon qu'il se trouve en dessus ou en dessous
de la valeur de référence.
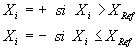 |
La valeur de référence correspond dans la plupart des cas à une valeur centrale (mode, moyenne, médiane) et on doit, pour que la comparaison soit valable, prendre la même valeur centrale pour chacune des distributions que l'on veut comparer. Cette valeur centrale doit être la plus représentative possible de l'ensemble des ditributions, de sorte que le choix de la moyenne n'a rien d'évident puisque l'on sait que cette valeur centrale n'est véritablement pertinente (n'offre un bon résumé) que pour les distributions unimodales symétriques. Le mode présente également de sérieux inconvénients (il peut y en avoir plusieurs). Aussi, dans la plupart des cas, c'est la médiane qui offre la meilleure solution lorsque l'on veut comparer plusieurs valeurs centrales à l'aide de cette méthode.
Dans l'exemple étudié (taille des villes et nombre de faute d'orthographe) le choix de la médiane s'impose de lui-même car les deux distributions X et Y sont fortement dissymétriques et la moyenne (surtout pour ce qui concerne la population) n'est pas du tout représentative (en raison de la valeur exceptionnelle de Paris).
Tableau 3 : discrétisation des caractères X et Y
| Code | X' | Y' |
| Bn | - | + |
| Bo | + | - |
| Bs | - | + |
| Ca | - | + |
| Cl | + | - |
| Di | - | + |
| Fo | - | + |
| La | - | - |
| Le | - | + |
| Li | + | - |
| Lm | - | + |
| Ly | + | - |
| Ma | + | - |
| Mo | + | + |
| Mx | - | - |
| Mz | - | + |
| Na | + | - |
| Ni | + | - |
| Or | - | + |
| Pa | + | - |
| Po | - | + |
| Re | - | - |
| Ro | + | + |
| St | + | - |
| To | + | - |
| + | : supérieur à la médiane | |
| - | : inférieur à la médiane | |
A l'aide du tableau 3, il est désormais beaucoup plus
facile de comparer les résultats de chaque ville et l'on voit se
dessiner une relation très claire entre la taille des villes et
leurs succès au concours d'orthographe. L'abondance des couples
(+,-) ou (-,+) et la rareté des couples (-,-) et (+,+) indique en
effet clairement que :
- plus les villes sont grandes moins leurs champions ont commis de fautes d'orthographes (+,-)
- plus les villes sont petites, plus elles ont commis de faute d'orthographe (-,+)
- il est rare qu'une petite ville ait commis peu de fautes d'orthographe (-,-)
- il est rare qu'une grande ville ait commis beaucoup de fautes d'orthographe (+,+)
Tableau 4 : distribution croisée des variables dichotomiques X et Y
| Fautes | |||
| Popul. | - | + | Total |
| - |
3
|
10
|
13
|
| + |
10
|
2
|
12
|
| Total |
13
|
12
|
25
|
La distribution des fréquences n'a apparemment rien d'aléatoire,
ce que l'on apprendra ultérieurement à démontrer sur
le plan statistique à l'aide du test d'indépendance du Chi-2
(Cf. Mise en relation de deux caractères qualitatifs).
Critique de la méthode dichotomique
Les résultats de la méthode dichotomique sont cependant
très simplifiés. Ainsi, deux villes ayant des valeurs très
proches peuvent apparaître classées différemment dans
le tableau de synthèse finale tandis que deux unités
éloignées peuvent être classées ensembles. De
plus, les résultats peuvent changer fortement selon le seuil retenu
comme valeur de référence. Si l'on avait utilisé la
moyenne plutôt que la médiane comme critère de discrétisation,
la relation entre la taille des villes et leur nombre de faute d'orthographe
serait apparu beaucoup moins nettement, comme le lecteur pourra le vérifier
par lui-même en repartant des données du tableau
1
et en reconstruisant des tableaux 3 et 4 établis par rapport
à la moyenne et non plus à la médiane.
Elargissement de la méthode dichotomique
Au lieu de ne faire que deux classes pour X et Y, on peut en faire plusieurs.
Il est cependant très important d'employer la même méthode
pour X et Y. Par exemple, on peut utiliser une discrétisation en
quatre modalités basée sur moyenne et écart-type.
Le tableau de contingence croisant les deux variables aura alors 16 cases.
On peut également utiliser les quartiles de la distribution pour
établir une discrétisation en quatre classes d'effectifs
égaux. L'essentiel est d'employer la même méthode
pour les deux caractères X et Y à comparer, faute de quoi
la comparaison des résultats ne serait plus valable.
5.2 TRANSFORMATION EN RANG
Une méthode aussi simple que la précédente
mais beaucoup plus robuste consiste à rendre les distributions comparables
en les transformant en classements (rangs) ce qui permet d'éliminer
les unités de mesure, les ordres de grandeur et les différences
de dispersion.
L'application de cette méthode ne soulève pose pas
de difficultés particulières mais il faut faire attention
à deux choses :
- l'ordre de classement (croissant ou décroissant) doit être spécifié et être si possible le même pour les deux caractères.
- lorsqu'il y a des ex-aequo, on leur attribue comme rang la moyenne des places qu'ils auraient occupé s'ils avaient été à la suite les uns des autres. On reprend ensuite le classement après les rangs virtiuellement occupés.
La question des ex-aequo ne se pose pas pour le caractère X (toutes les villes ont des population différentes) mais elle apparaît à plusieurs reprises pour le caractère Y. Ainsi, 5 villes ont commis 9.5 fautes d'orthographes et occupent implicitement les rangs de 13e, 14e, 15e, 16e et 17e. Plutôt que de leur attribuer toutes le rang de 13e (ce que l'on ferait dans une compétition sportive), le statisticien leur attribuera la moyenne des rangs c'est-à-dire la place de 15e à toutes les cinq. On remarquera incidemment que cette manière de procéder est plus rigoureuse que la méthode "sportive". Enfin, on prendra garde lorsque l'on passera à la ville suivant les cinq précédentes de lui attribuer le rang de 18e et non pas de 16e car d'un point de vue statistique, il est essentielle que la somme des rangs attribués à N individus soit bien égale à la somme des N premiers entiers soit 1+2+3+....+N = N(N+1)/2.
Tableau 5 : Transformation ordinale des caractères X et Y
| Code | Popul. | Fautes |
| Bn |
20
|
4
|
| Bo |
5
|
22.5
|
| Bs |
24
|
7
|
| Ca |
18
|
6
|
| Cl |
11
|
20
|
| Di |
14
|
10.5
|
| Fo |
22
|
1
|
| La |
25
|
15
|
| Le |
16
|
12
|
| Li |
4
|
15
|
| Lm |
19
|
2
|
| Ly |
2
|
15
|
| Ma |
3
|
18.5
|
| Mo |
12
|
5
|
| Mx |
23
|
22.5
|
| Mz |
17
|
10.5
|
| Na |
7
|
15
|
| Ni |
8
|
18.5
|
| Or |
13
|
8.5
|
| Pa |
1
|
22.5
|
| Po |
21
|
3
|
| Re |
15
|
15
|
| Ro |
9
|
8.5
|
| St |
10
|
22.5
|
| To |
6
|
25
|
Le tableau 5 obtenu en transformant le tableau 1 en classement est simple à interpréter et beaucoup plus précise que celui qui avait été obtenu par la méthode de discrétisation dichotomique (tableau 3). Quelle que soit la ville choisie, on peut immédiatement savoir si les classements sont identiques ou différents sur les deux critères retenus. En règle général on observe de très forts écarts entre les deux classements sauf pour les individus situés en position médiane. Ceci confirme l'hypothèse d'une relation négative entre les deux variables X et Y : plus une ville est grande, moins ses champions ont commis de fautes d'orthographe et, réciproquement, plus une ville est petite, plus ses champions ont commis de fautes d'orthographe au concours de France 3.
On verra au chapitre suivant que cette hypothèse d'une relation
statistique entre les rangs des individus pour deux caractères quantitatifs
peut être testée à l'aide du coeffcient de corrélation
de Spearman qui est précisément fondé sur l'analyse
des différences de rang et permet de détecter des relations
linéaires ou non-linéaires monotones entre deux caractères
quantitatifs.
Cette méthode de comparaison est sans conteste l'une des meilleures
voire la meilleure lorsque les distributions étudiées ne
sont pas unimodales et symétriques. Mais elle possède
tout de même l'inconvénient d'éliminer totalement l'ordre
de grandeur des caractères étudiés. deux individus
proche sur un caractère peuvent se retrouver très éloignés
en terme de rangs, s'ils se trouvent situés dans une zone de la
distribution ou les valeurs sont très rapprochées. Ainsi,
Le Havre (10 fautes) et Clermont-Ferrand (8.5 fautes) ont une différence
de classement considérable (respectivement 12e et 20e) simplement
parce que beaucoup de villes ont commis 9 ou 9.5 fautes. Inversement Fort-deFrance
et Limoges occupe des rangs successifs (1er et 2e) alors que leur différence
absolue de fautes est considérable (respectivement 33 et 21.5).
5.3 TRANSFORMATION EN INDICE
La méthode des indices semble de prime abord plus satisfaisante
que la précédente puisque précisément elle
conserve l'ordre de grandeur des caractères tout en les ramenant
à une base commune appelée indice et dont la valeur est généralement
fixée à 100.
Très employée en économie, cette méthode
consiste à définir une valeur de référence
et à exprimer toutes les variables dans une unité de mesure
commune (appelée base de l'indice) exprimant l'écart à
la valeur de référence sous la forme d'un rapport. On choisit
en général le moyenne comme valeur de référence
et la valeur 100 comme base de l'indice.
Le tableau des indices permet immédiatement de voir la position
des individus par rapport à la valeur de référence
choisie. Ainsi, si cette valeur est la moyenne :
- un indice 110 signifie que l'individu est situé 10% au dessus de la moyenne
- un indice 80 signifie que l'individu est situé 20% au dessous de la moyenne
- etc.
ex. de 1950 à 1980, la France passse de 42 à 54 millions d'habitants et l'Albanie de 1.2 à 2.7 millions d'habitants. Si l'on prend comme indice 100 la population en 1950, on trouve qu'en 1980 la France est à l'indice 129, tandis que l'Albanie est à l'indice 225.
Mais on doit prendre garde au fait que le choix de la date de référence
(indice 100) exerce une grande influence sur les résultats et qu'un
accroissement de 10% (passage de l'indice 100 à l'indice 110) ne
compense pas une baisse de 10% (passage de l'indice 100 à l'indice
90). Pour plus de détails sur ce point, se reporter au chapitre
sur les séries chronologiques.
Malgré les habitudes paresseuses de beaucoup de journalistes
et d'économistes, on ne doit pas privilégier obligatoirement
la moyenne dans le calcul des indices et il peut souvent s'avérer
beaucoup plus pertinent de prendre la médiane comme valeur de référence.
Dans l'exemple étudié, il est beaucoup plus pertinent de
choisir la médiane pour comparer le nombre de fautes d'orthographe
et la taille des villes (Cf. remarques sur
le choix d'un seuil de discrétisation). On construira donc un
indice 100 égal à la médiane des distributions et
non pas à leur moyenne (Tableau
6).
Tableau
6 : Transformation des caractères X et Y
en indice 100 par rapport à la médiane
| Code | Popul. | Fautes |
| Bn |
55
|
189
|
| Bo |
291
|
84
|
| Bs |
23
|
142
|
| Ca |
84
|
147
|
| Cl |
116
|
89
|
| Di |
98
|
116
|
| Fo |
45
|
347
|
| La |
7
|
100
|
| Le |
87
|
105
|
| Li |
425
|
100
|
| Lm |
78
|
226
|
| Ly |
555
|
100
|
| Ma |
505
|
95
|
| Mo |
100
|
168
|
| Mx |
25
|
84
|
| Mz |
85
|
116
|
| Na |
211
|
100
|
| Ni |
204
|
95
|
| Or |
100
|
132
|
| Pa |
3958
|
84
|
| Po |
47
|
205
|
| Re |
90
|
100
|
| Ro |
173
|
132
|
| St |
170
|
84
|
| To |
246
|
74
|
Avec un peu d'habitude la lecture des tableaux d'indice est rapide et performante. Ainsi on voit immédiatement que Lyon est au moins 5 fois plus peuplée que la moitié des villes étudiées (indice 505 pour la population) mais que son niveau d'orthographe (indice 100 pour les fautes) se situe dans une honnête médiane sans plus. Ou bien, Poitiers apparaît comme une ville assez petite dans l'échantillon d'étude (indice 47) et avec un nombre de faute très élevé (indice 205) tandis que Toulouse à des caractéristiques paratiquement inverse.
En fait, la transformation en indice (tableau
6) peut être considéré comme une variante plus
précise de la discrétisation dichotomique (tableau
3) puisque dans l'un et l'autre cas l'idée est de positionner
les valeurs par rapport à une valeur de référence
et de mesurer les écarts de façon discrète ('+' /
'-') ou de façon continue et relative (indice supérieur ou
inférieur à 100.
Critique
Intéressante à certains égards, la méthode
des indices n'est cependant pas à recommander d'un point de vue
statistique car elle n'est pas très objective et permet toutes sortes
de manipulations. Le choix de la valeur de référence est
en effet crucial et peut considérablement modifier les résultats
(comme dans le cas de la discrétisation). De plus, cette méthode
possède le grave inconvénient de ne pas tenir compte de la
dispersion des caractères et elle ne fait que corriger l'ordre de
grandeur. Or, il existe une méthode beaucoup plus efficace, la standardisation,
qui tient compte des deux paramètres à la fois et assure
des comparaison de qualité nettement supérieure.
5.4 STANDARDISATION
La standardisation est la méthode la plus efficace
de comparaison de deux variables lorsque ces dernières sont unimodales
et symétriques. Elle consiste à opérer une double
transformation de centrage et de réduction (les variables standardisées
sont aussi appelées variables centrées-réduites).
- Le centrage consiste à ramener l'ordre de grandeur (valeur centrale) de la distribution des valeurs à une valeur de référence fixée par l'utilisateur et que l'on choisit en général égale à 0. L'intérêt d'un centrage sur 0 est de pouvoir immédiatement repérer à l'aide du signe (+/-) les individus situés en dessus ou en dessous de la valeur de référence.
- La réduction consiste à ramener l'hétérogénéité (paramètre de dispersion) de la distribution des valeurs à une seconde valeur de référence, également fixée par l'utilisateur, et que l'on choisit en général égale à 1. L'intérêt de la réduction est de rendre immédiatement comparable les écarts positifs ou négatifs par rapport à la valeur de référence qui a été fixée et de raisonner toutes choses égales quant à la dispersion de chaque distribution.
La solution la plus fréquemment employée en matière
de standardisation est le centrage par rapport à la moyenne
et la réduction par rapport à l'écart-type.
Lorsque l'on parle de standardisation sans autre précision, cela
signifie implicitement que l'on a employé la formule suivante
:
Une variable X' standardisée par rapport à la moyenne
et à l'écart-type sera donc caractérisée par
le fait que sa moyenne est égale à 0 et son écart-type
est égal à 1. Cette double propriété faculite
considérablement l'interprétation de la position des individus
puisque l'on peut désormais raisonner par rapport à une distribution
de référence (la distribution gaussienne) et savoir immédiatement
:
- si un individu est situé en dessus ou en dessous de la moyenne (signe de la valeur standardisée positif ou négatif)
- si un individu est caractérisé par une valeur du caractère banale ou exceptionnelle (valeur absolue de la variable standardisée proche de 0 ou éloignée de 0).
| Code | Popul. | Fautes |
| Bn |
-0.3
|
1.0
|
| Bo |
0.0
|
-0.7
|
| Bs |
-0.4
|
0.2
|
| Ca |
-0.3
|
0.3
|
| Cl |
-0.3
|
-0.6
|
| Di |
-0.3
|
-0.2
|
| Fo |
-0.4
|
3.6
|
| La |
-0.4
|
-0.5
|
| Le |
-0.3
|
-0.4
|
| Li |
0.2
|
-0.5
|
| Lm |
-0.3
|
1.6
|
| Ly |
0.3
|
-0.5
|
| Ma |
0.3
|
-0.6
|
| Mo |
-0.3
|
0.7
|
| Mx |
-0.4
|
-0.7
|
| Mz |
-0.3
|
-0.2
|
| Na |
-0.1
|
-0.5
|
| Ni |
-0.1
|
-0.6
|
| Or |
-0.3
|
0.1
|
| Pa |
4.8
|
-0.7
|
| Po |
-0.3
|
1.3
|
| Re |
-0.3
|
-0.5
|
| Ro |
-0.2
|
0.1
|
| St |
-0.2
|
-0.7
|
| To |
-0.1
|
-0.9
|
En se rappelant ce qui a été dit sur l'écart-type et la distribution gaussienne au chapitre précédent on voit immédiatement que ce tableau permet de positionner chaque individu par rapport à une grille de lecture commune à l'ensemble des variables et qu'il devient alors très facile de décrire de façon qualitative mais objective les positions relatives des individus sur chaque variable (par référence à la distribution gaussienne).
Tableau 8 : grille de lecture qualitative des valeurs standardisées
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Appliquée au tableau 7, cette grille de lecture permet de commenter facilement la position de chaque ville sur les deux critères considérés. Ainsi, on peut dire que Le Mans a une population assez faible par rapport aux autres villes de l'échantillon considérée (-0.3) et un nombre de fautes d'othographe élevé (+1.6).
Mais les résultats sont dans l'ensemble assez décevant car on remarque vite que la plupart des villes ont des valeurs standardisées comprises entre -1 et +1 sur chacun des deux critères. Ce résultat tient à la présence de deux valeurs exceptionnellement fortes, l'une dans la distribution de spopulations (Paris : + 4.8) et l'autre dans la distribution des fautes d'orthographe (Fort-de-France : + 3.6). Ces deux valeurs exceptionnelles rendent les distributions fortement dissymétriques et, du coup, rendent peu pertinent le choix de la moyenne et de l'écart-type comme critère de standardisation.
Critique
La standardisation est en théorie la méthode la plus puissante
pour comparer différentes distributions, mais elle n'est pleinement
valable (dans sa forme classique) que lorsqu'elle est appliquée
à des distributions unimodales et symétriques. Si ce n'est
pas le cas il vaut mieux :
- Soit procéder à une standardisation utilisant la médiane comme valeur de référence et l'intervalle interquartile (divisé par deux) comme paramètre de dispersion.
- Soit utiliser la méthode des rangs qui est plus robuste face à la présence de valeurs exceptionnelles.
CONCLUSION
La standardisation et les autres méthodes permettent de comparer la distribution de plusieurs caractères quantitatifs continus, même si ceux-ci possèdent des unités de mesure différente, des valeurs centrales différentes, des paramètres de dispersion différents. Le choix de la méthode la meilleure dépend de l'objectif, du destinataire et des propriétés de la distribution.
Dans le cas où l'on étudie deux variables quantitatives
continues X et Y, la standardisation permet de détecter la présence
de relations entre les variables, que celles-ci soit positives ou négatives.
Elle constitue donc le préalable indispensable au test d'hypothèses
sur l'existence de relations statistiquement significatives (corrélation)
ou à la mise en place de modèles d'estimation des valeurs
d'une variable par rapport à une autre (régression) que nous
verrons dans les chapitres suivants.