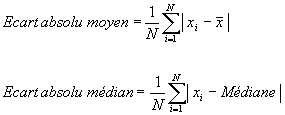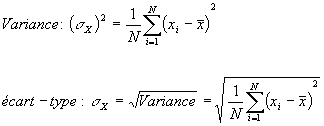Le résumé d'une distribution que donne une valeur centrale ne nous renseigne pas sur la dispersion des valeurs autour de cette valeur centrale, c'est-à-dire sur la tendance qu'elles-ont à se concentrer ou se disperser autour de celle-ci.
Exemple : Si l'on considère deux professeurs X et Y chargés de noter 9 élèves, peut-on apprécier leur manière de noter simplement en regardant la moyenne, la médiane ou le mode de leurs notes ?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=> A s'en tenir à l'analyse des valeurs centrales, on serait amené à conclure que les deux Pr X et Y notent rigoureusement de la même manière (moyenne=médiane=mode=10) mais on sent bien intuitivement que ce n'est pas le cas et qu'il existe une différence dans leur style de notation. Cette différence tient au fait que le professeur X "concentre" ses notes autour de 10 alors que le professeur Y "disperse" davantage ses notes autour de la valeur de référence.Il est donc utile de compléter les valeurs centrales par un paramètre de dispersion absolue qui donne un ordre de grandeur de l'écart des valeurs entre elles ou, ce qui revient au même, de l'écart des valeurs à la valeur centrale de référence.
On appelle dispersion statistique, la tendance qu'ont les valeurs de la distribution d'un caractère à s'étaler de part et d'autre d'une valeur centrale et/ou à s'éloigner les unes des autres. Ce calcul n'a évidemment de sens que pour les caractères quantiatifs.
On distingue les paramètres
de dispersion absolue (mesurée dans l'unité de mesure
du caractère) et les paramètres
de dispersion relative (mesurée par un nombre sans dimension).
4.2 LES PARAMETRES DE DISPERSION ABSOLUE
Les paramètres de dispersion absolue indiquent de
combien les valeurs d'une distribution s'écartent en général
de la valeur de référence. Un paramètre de dispersion
absolue s'exprime toujours dans l'unité de mesure de la variable
considérée. Ainsi, si l'on étudie la densité
de population des régions européennes, l'unité de
mesure de la dispersion de ce caractère sera exprimée en
habitants par km2.
Les quatre paramètres de dispersion absolue les plus courants sont l'étendue, l'intervalle interquartiles, l'écart absolu moyen et l'écart type.
4.2.1 Etendue
Définition : l'étendue d'une distribution est égale à la différence entre la plus grande et la plus petite valeur de la distribution :4.2.2 Quantiles
Etendue de X = Xmax-Xmin Exemple : Notation des professeurs X et Y :
- L'étendue des notes données par le professeur X est de (13-7)=6, ce qui signifie que l'écart maximum entre deux notes du professeur X est de 4.
- L'étendue des notes données par le professuer Y est de (20-0)=20 ce qui signifie que l'écart maximum entre deux notes du professeur Y est de 20
=> La dispersion des notes du professeur Y est donc beaucoup plus forte que celle des notes du professeur X.
L'inconvénient de l'étendue est qu'elle dépend uniquement des deux valeurs les plus extrêmes de la distribution. Elle indique donc la différence maximum entre deux valeurs mais pas la différence typique.
Exemple : Salaires de l'entreprise Zykosar
L'étendue de la distribution des salaires dans l'entreprise Zykosar est de (100000 - 1300) = 98700 CR $ ce qui semble considérable. Mais si l'on retirait le directeur et les sous-directeur, l'amplitude des salaires ne serait plus que de (5500-1300)=4200 CR $. En dehors des trois dirigeant, les salariés de l'entreprise Zykosar ont donc des salaires très peu différenciés.Conclusion : l'étendue est un paramètre de dispersion absolue qui est simple à calculer mais très fragile puisqu'il ne dépend que de deux valeurs de la distribution. Ce paramètre n'a guère de signification lorsqu'une distribution comporte des valeurs exceptionnelles.
Pour remédier aux inconvénients de l'étendue, on peut retirer les valeurs les plus extrêmes et calculer l'intervalle des valeurs restantes : c'est la base de la méthode des quantiles.4.2.3 Ecart absolu moyen / Ecart absolu médianOn appelle quantiles les bornes d'une partition en classes d'effectifs égaux. Attention, lorsqu'on utilise les quantiles, ce sont les effectifs qui sont égaux et non pas les amplitudes. (Cf. Dénombrement des caractères continus 2.2)
- Les quartiles par exemple, sont les trois valeurs qui permettent de découper la distribution en quatres classes d'effectifs égaux, on les note Q1, Q2 et Q3.
Classes fréquence simple [Xmin ; Q1 [ 25 % [Q1 ; Q2 [ 25 % [Q2 ; Q3 [ 25 % [Q3 ; Xmax ] 25 % - L'intervalle interquartile (Q3-Q1) est un paramètre de dispersion absolue qui correspond à l'étenude de la distribution une fois que l'on a retiré les 25% des valeurs les plus faibles et les 25% des valeurs les plus fortes. 50% des observations sont donc concentrées entre Q1 et Q3.
1ere méthode pour déterminer les quartiles (utilisation de la médiane)
On remarque que le second quartile (Q2) d'une distribution X est égale à la médiane Med(X) de cette distribution. On détermine cette valeur à l'aide des méthodes exposées précédemment (Cf. calcul des valeurs centrales) puis on découpe la distribution X en deux demi-distributions X' et X" correspondant respectivement aux valeurs supérieures ou inférieures à la médiane.
On remarque alors que Q1 est égal à la médiane de la distribution X' et que Q3 est égal à la médiane de la distribution X", valeurs qui peuvent être obtenues sans difficultés.
Le seul problème de cette méthode concerne l'établissement des deux demi-distributions X' et X" lorsque le nombre d'observation est impair. La médiane correspondant alors à une valeur du caractère, on devra la placer dans chacune des demi-distributions pour trouver ensuite Q1 et Q3.
Exemple : Notation des professeurs X et Y :
Pour le professeur X, on calcul la médiane qui est la valeur du 5e élément de la distribution (10) et on construit les deux distributions X'={7,8,9,10,10} et X"={10,10,11,12,13} qui correspondent aux 50% des valeurs les plus faibles et aux 50% des valeurs les plus fortes. Q1 est égal à la médiane de X', soit 9. Q3 est égal à la médiane de X", soit 11. L'intervalle interquartile est donc égal à (Q3-Q1)=2.
=> on en déduit que 50 % des élèves ont des notes concentrées entre 9 et 11, c'est-à-dire sur un intervalle de 2 points.Le même calcul effectué pour les notes du professeur Y aboutit aux même valeurs Q1=9, Q3=11 et (Q3-Q1)=2. Pour le critère retenu, la dispersion des deux distributions X et Y est donc la même puisque, pour le professeur X comme pour le professeur Y on constate que 50% des notes sont concentrées sur un intervalle de 2 points.
2e méthode pour déterminer les quartiles (utilisation des fréquences cumulées)
Une seconde méthode plus générale pour déterminer n'importe quel quantiles (et pas seulement les quartiles) consiste à utiliser la courbe des fréquences cumulées ascendantes .
Par définition, les fréquences cumulées correspondant aux quartiles sont en effet les suivantes :
Fcum(Q1) = 25%
Fcum(Q2) = 50 % (médiane)
Fcum(Q3) = 75 %Il suffit donc de lire sur la courbe des fréquences cumulées les valeurs approximatives correspondant à Q1, Q2 et Q3 ou à procéder à une interpolation linéaire entre les bornes d'une partition en classes pour trouver les valeurs exactes.
Exemple : Salaires de l'entreprise Zykosar
Après avoir établi la courbe des fréquences cumulées des salaires de l'entreprise Zykosar, à l'aide du tableau élémentaire (Cf. Chapitre 2, Figure 6), on détermine graphiquement les valeurs de Q1=2000 CR$, Q2=2800 CR$ et Q3=4750 CR$. On remarque toutefois que la précision serait beaucoup plus médiocre si l'on avait utilisée la courbe des fréquences cumulée établie à l'aide d'une partition en classes. En effet la partition en classe introduit une perte d'information (on ignore la répartition des individus dans les classes) et l'interpolation linéaire peut surestimer ou sous-estimer la valeur réelle des paramètres (l'estimation de Q3 serait ainsi de 40000 CR$ à l'aide de la courbe des fréquences cumulées établie à partir de la partition en classes).
Au total, on aboutit à la conclusion que la dispersion des salaires de l'entreprise Zykosar est relativement faible puisque la moitié des salariés sont concentrés sur un intervalle de salaire de 2750 CR$ (Q3-Q1) une fois que l'on a retiré les 25% des salaires les plus faibles (moins de 2000 CR$) et les 25% des salaires les plus forts (plus de 4750 CR$).
Bien que les quartiles soient les plus utilisés, on peut également utiliser d'autres découpages d'effectifs égaux :
- les quintiles partagent une distribution en cinq classes d'effectifs égaux et sont très utilisés en cartographie.
- les déciles partagent une distribution en dix classes d'effectifs égaux. L'intervalle compris entre le premier décile et le dernier décile est l'intervalle interdéciles (D9-D1). L'intervalle interdéciles est l'amplitude de la distribution une fois retirée les 10% de valeur les plus fortes et les 10% de valeurs les plus faibles.
Exemple : Salaires de l'entreprise Zykosar
Caculer l'intervalle interdécile revient à déterminer l'entreprise de la distribution une fois que l'on a retiré les 10% des salariés qui gagnent le plus et les 10% des salariés qui gagnent le moins. Dans l'exemple considéré les valeurs respectives de D1 et D9 sont de 1400 CR$ et 25000 CR$. L'intervalle décile (tranche de salaire regroupant 80% des salariés) est donc de 23100 CR$.
Définition : l'écart absolu moyen est la moyenne de la valeur absolue des écarts à la moyenne. Autrement dit, c'est la distance moyenne à la moyenne. Bien qu'il soit moins utilisé, on peut calculer de la même manière l'écart absolu médian qui est la moyenne des écarts à la médiane.4.2.4 Ecart-typeFormules de l'écart absolu moyen et de l'écart absolu médian
L'intérêt de ces deux valeurs centrales est d'être faciles à calculer et simples à interpréter. Malheureusement, elles ne sont pas fournies par la plupart des logiciels de statistiques et l'écart-type est beaucoup plus utilisé, bien que son interprétation soit beaucoup moins évidente.
Exemple : Notation des professeurs X et Y :
Le calcul de l'écart absolu moyen des notes du Pr X est obtenues en effectuant la moyenne de la valeur absolue des écarts à la moyenne :
Calcul de l'écart absolu moyen des notes du Pr X
i xi A 7 3 B 8 2 C 9 1 D 10 0 E 10 0 F 10 0 G 11 1 H 12 2 I 13 3 total 90 12 moyenne 10 12/9 = 1.33 L'écart absolu moyen de la notation du professeur X est donc de 1.3, ce qui signifie que les notes s'écartent en moyenne de 1.3 de la moyenne. Il n'y a donc pas, en moyenne, de gros écarts à la moyenne. Si on effectue le même calcul pour le professeur Y, on trouve un écart absolu moyen de 3.6, ce qui signifie que ses notes s'écartent généralement beaucoup plus de la moyenne. On peut donc conclure que la dispersion des notes du Pr Y est plus forte que celle du Pr X.
4.2.5 Paramètres de dispersion absolue et valeurs centrales.
Définition : l'écart-type est la racine carrée de la variance, elle-même définie comme la moyenne du carré des écarts à la moyenne :Formules de la variance et de l'écart-type
La variance n'est pas à proprement parler un paramètre de dispersion absolue mais plutôt une mesure globale de la variation d'un caractère, c'est-à-dire de la quantité moyenne d'information contenue dans les différentes valeurs de ce caractère : cette quantité d'information serait évidemment nulle si toutes les valeurs étaient égales et elle est d'autant plus élevée que ces valeurs sont différentes les unes des autres. On observera que dans la perspective de la théorie de l'information, la formule précédente de la variance est incorrecte car elle ne tient pas compte de l'information connue (moyenne). Une formulation plus exacte de la variance consiste à diviser la somme des carrés des écarts (SCE) par le nombre de degrés de liberté, c'est-à-dire le nombre d'observations (N) moins le nombre de paramètre (1). Il conviendrait donc, dans cette perspective, de remplacer le terme 1/N par le terme 1/(N-1) dans les équations précédentes. Cette correction qui est indispensable lorsque l'on procède à des tests statistiques (Fischer, Student), n'est pas indispensable dans une perspective de statistique purement descriptive.
L'écart-type est le paramètre de dispersion absolue le plus utilisé en statistique et il est fourni par tous les logiciels d'analyse des données, y compris les plus simples (calculatrice de poche). Sa signification est cependant loin d'être évidente (moyenne quadratique des écarts à la moyenne) et de nombreuses personnes le confondent avec l'écart absolu moyen qui est quant à lui d'interprétation simple (moyenne des écarts à la moyenne).
Sans entrer dans des détails théoriques qui dépassent le cadre de cet enseignement, les utilisateurs de l'écart-type doivent être conscient que l'utilisation de celui-ci n'est pleinement justifié que dans le cas ou la distribution des valeurs de la distribution observé est de forme gaussienne ou, à tout le moins, symétrique et unimodale.
En effet, dans le cas où la forme de la distribution observée est de type gaussien (mais dans ce cas seulement !) l'écart-type peut revêtir une signification probabiliste et servir à définir des intervalles de confiance autour de la moyenne.
intervalle % des valeurs d'une distribution gaussienne moyenne + ou - 1 68.3% moyenne + ou - 2 95.5% moyenne + ou - 3 99.7%
Exemple : Notation des professeurs X et Y :
Pour déterminer l'écart-type des notes du Pr X, il convient tout d'abord de calculer leur variance, c'est-à-dire la moyenne du carré des écarts à la moyenne :
Calcul de la variance des notes du Pr X
i xi A 7 9 B 8 4 C 9 1 D 10 0 E 10 0 F 10 0 G 11 1 H 12 4 I 13 9 total 90 12 moyenne 10 var = 26/9 = 3.11 La variance des notes du Pr X étant de 3.11, on en déduit la valeur de l'écart-type (1.8) en calculant la racine carré de cette variance. Cette valeur de 1.8 peut être considérée comme une mesure de l'ordre de grandeur de la dispersion des notes autour de la moyenne. Si la distribution des notes du Pr X était gaussienne (ce qui est difficile à affirmer au vu de la faiblesse de l'échantillon) on devrait trouver environ deux tiers des notes dans l'intervalle [8.2 ; 11.8] qui correspond à la moyenne plus ou moins un écdart-type et 95% des notes dans l'intervalle [6.4 ; 13.8] qui correspond à la moyenne plus ou moins deux écarts-type.
Le même calcul effectué sur les notes du Pr Y aboutit à un écart-type de 5.3 qui est beaucoup plus importante que celui des notes du professeur X. On retrouve la conclusion obtenue à l'aide de l'écart absolu moyen : les notes du Pr Y sont beaucoup plus dispersées que celles du Pr X.
4.2.6 Valeurs centrales, paramètres de dispersion et choix d'une partition en classes
Le résumé d'une distribution par une valeur centrale est souvent trompeur parce qu'il est incomplet : on connaît l'ordre de grandeur des valeurs mais on ignore la dispersion des valeurs autour de la valeur centrale de référence. Le premier rôle des paramètres de dispersion est donc d'accompagner et de préciser les résumés de distribution effectués à l'aide des valeurs centrales.Exemple : Salaires de l'entreprise Zykosar
Nous avons vu dans le chapitre précédent que la moyenne (10000 CR$) offrait un résumé très trompeur des salaires de l'entreprise Zykosar et que la médiane ou le mode étaitent beaucoup plus représentatives de la réalité de la distribution. Mais les inconvénients de la moyenne auraient été sensiblement réduits si elle avait été accompagnée d'un paramètre de dispersion tel que l'écart absolu moyen (20500 CR$) ou l'écart-type (46500$). Ces derniers auraient en effet montré d'emblée les fortes inégalités de salaire existant dans l'entreprise et auraient permis à l'observateur d'en déduire immédiatement l'existence d'une minorité de salaires très supérieurs à la moyenne et d'une majorité de salaires inférieurs à la moyenne.
Un bon résumé statistique doit donc toujours comporter au moins deux paramètres : une valeur centrale et un paramètre de dispersion. L'appariement des valeurs centrales et des paramètres de dispersion ne peut toutefois pas s'effectuer de n'importe quelle manière et certaines associations peuvent se faire de façon privilégée.
- la moyenne peut-être accompagnée soit de l'écart-type, soit de de l'écart absolu moyen (puisque ces paramètres sont calculés par rapport à la moyenne)
- la médiane peut-être accompagnée soit de l'écart absolu médian, soit de l'intervalle interquartile ou de l'intervalle interdécile.
- Le mode, qui n'est véritablement utile que dans le cas des distributions multimodales, peut être accompagnée de l'étendue (qui est le seul paramètre de dispersion conservant une signification dans le cas des distributions multimodales).
Pour des raisons pédagogique, nous avons placé le chapitre consacré au dénombrement et aux représentations graphiques (Chap.2) avant ceux consacrés aux valeurs centrales (Chap.3) et aux paramètres de dispersion (Chap.4). Nous avons été ainsi amener à proposer un certain nombre de méthodes de partitions d'un caractère quantitatif continu en classes indépendantes du calcul des valeurs centrales et des paramètres de dispersion (seuils naturels, effectifs égaux, amplitudes égales).Il convient de revenir brièvement sur ce point car, dans la pratique et notamment lorsque l'on veut comparer plusieurs distributions (cartes, histogrammes) on établit des méthodes de partitions en classes fondées sur les valeurs centrales ou les paramètres de dispersion absolue des distributions.
Ainsi, la méthode de découpage des classes à l'aide des seuils naturels convient bien lorsque l'on veut étudier une seule distribution.Mais lorsque l'on veut comparer deux distributions, il est préférable de recourir à des principes de découpage qui soient les mêmes pour les deux distributions. Comme les seuils naturels respectent les particularités de chacune des deux distributions, ils ne permettent pas la comparaison.
Les paramètres de dispersion absolue et les valeurs centrales permettent au contraire d'établir des partitions comparables pour différents caractères.
Classes d'amplitudes égales établies à partir de l'étendue
- On fixe a priori le nombre K de classes que l'on souhaite établir, puis l'on divise la distribution en K classes dont l'amplitude est égale à (Etendue/K) en allant du minimum au maximum.
Exemple : si une distribution va de 10 à 170 (amplitude=160) et que l'on souhaite établir 4 classes, celles-ci auront une amplitude de 160/4=40 et seront donc [10;50[,[50;90[,[90;130[, [130;170]
Il est à noter que les valeurs centrales peuvent se trouver dans n'importe laquelle des classes et n'interviennent pas dans la détermination de celles-ci. On peut donc avoir des surprises désagréables sous la forme de classes vides successives.
Exemple : dans l'exemple ci-dessus, si les valeurs de la distribution étaient 10,10,20,20,30,30,40,170, les deuxième et troisième classes seront vides.
Classes d'amplitudes inégales mais d'effectifs égaux (quantiles)
- Comme précédemment, on fixe a priori le nombre de classe, mais au lieu de faire des classes d'amplitudes égales ont fait des classes d'effectifs égaux dont les bornes sont les quantiles correspondant au nombre K de classes choisis. L'effectif de chaque classe sera évidemment N/K.
Exemple : si l'on reprend la distribution précédente, l'établissement de 4 classes d'effectifs égaux se fait à partir des quartiles de la distribution soit [10;15[,[15;25[,[25;35[ et [35;170].
Classes utilisant l'écart-type et la moyenne
Le principe général est que l'amplitude des classes est égales (sauf pour les classes extrèmes) et qu'elle dépend de l'écart-type. Par exemple, on décidera que toutes les classes auront une amplitude de 1 écart-type.
La moyenne quant à elle sert à caler la position des classes. On distingue deux cas :
* la moyenne sert de centre de classe : le nombre de classe est alors généralement impair. Un cas très fréquent est celui de la partition en cinq classes d'amplitude établies sur le modèle suivant :
[xmin ;
- 1.5
[
[- 1.5
;
- 0.5
[
[- 0.5
;
+0.5
[
[+0.5
;
+1.5
[
[+ 1.5
; x max]
* la moyenne sert de limite de classe : le nombre de classe est alos généralement pair. Un cas fréquent est celui de la partition en 6 classes (les classes extrêmes pouvant être vides) :
[xmin ;
- 2
[
[- 2
;
-
[
[-
;
[
[;
+
[
[+
;
+2
[
[+ 2
; x max]
Classes utilisant la moyenne et l'écart absolu moyen
Le principe est le même que pour les classes établies à partir de la moyenne et de l'écart-type, si ce n'est que l'on utilise l'écart absolu moyen à la place de l'écart-type.
Classes utilisant la médiane et l'écart absolu médian
Le principe est le même que pour les classes établies à partir de la moyenne et de l'écart-type, si ce n'est que l'on utilise l'écart absolu médian à la place de l'écart-type et la médiane à la place de la moyenne.
N.B. : il existe encore d'autres solutions, par exemple en combinant la médiane et l'écart absolu moyen ou en réalisant des classes équiprobables ...
Ce qu'il faut retenir :
- Lorsque l'on veut comparer deux distributions, les seuils naturels ne sont pas adaptés et il faut un même principe de partition pour les deux distributions.
- Les classes établies en fonction de la moyenne et de l'écart-type sont les plus utilisées et les plus performantes, à condition que les distributions soient unimodales et symétriques.
- Les classes établies en fonction des quantiles sont bien adaptées au cas des distributions fortement dissymétriques.
- Les classes sont aussi le reflet d'une problématique. Dans certains cas, on fixera les classes en fonction de la connaissance que l'on a du phénomène et non selon des considérations statistiques. Ainsi, pour un indice de fécondité, la valeur 2.1 enfant par femme est une borne pertinente car elle correspond au niveau de remplacement des générations. De même,pour un taux d'accroissement, la valeur 0 est pertinente car elle sépare croissance et décroissance. On peut donc être amené à retenir ces bornes, même si elles ne correspondent pas à un paramètre statistique.
- Toute partition est accepatable a priori si les choix sont explicités et justifiés !