Chapitre 6 : LA CORRELATION

 

 

INTRODUCTION
6.1 TYPES DE RELATION
6.2 CALCUL DES COEFFICIENTS DE CORRELATION
6.3 SIGNIFICATIVITE D'UNE RELATION
6.4 CORRELATION ET CAUSALITE
 
 

Menu général

Chapitre précédent

Chapitre suivant

 

INTRODUCTION

 Relation et dépendance

Soit deux caractères quantitatifs X et Y, décrivant le même ensemble d'unités. On dit qu'il existe une relation entre X et Y si l'attribution des modalités de X et de Y ne se fait pas au hasard, c'est à dire si les valeurs de X dépendent des valeurs de Y ou si les valeurs de Y dépendent des valeurs de X. Dire que Y dépend de X signifie que la connaissance des valeurs de X permet de prédire, dans une certaine mesure, les valeurs de Y. En d'autres termes, si Y dépend de X, on peut trouver une fonction f telle que :

Y=f(X)
 

Exemple : il existe une relation entre la température et l'altitude. La dépendance entre la température et l'altitude est exprimée par la relation :

Tz = -0.6*Z + T0

avec
Tz : température à l'altitude z
Z : altitude en centaines de mètres
T0 : température au niveau de la mer.
 

La notion de dépendance n'est pas symétrique :

Lorsque l'on écrit Y=f(X), on postule que Y est la variable dépendante (à expliquer) et que X est la variable indépendante (explicative). Celà signifie que les valeurs de X permettent de prédire les valeurs de X, mais il n'est pas certain que la réciproque soit vraie.

Exemple : La théorie de l'optimum de taille des villes
 

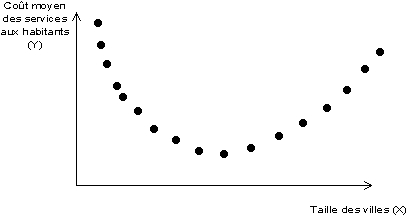
D'après cette théorie, il existe une taille optimale des villes qui minimise les coûts d'équipement : les villes trop petites ne permettent pas de réaliser d'économies d'échelles, les villes trop grandes entraînent des surcôuts liés à la congestion des réseau et à la durée des déplacements quotidiens.
=> Si cette théorie est vraie, on peut montrer que les côuts dépendent de la taille (la connaissance de X permet de prédire la valeur de Y).
=> en revanche, la taille ne dépend pas des coûts ( des coûts élevés peuvent correspondre soit à des grandes villes soit à des petites villes : la connaissance des coûts ne permet pas de prévoir la taille).
 
 

LES TYPES DE RELATIONS ENTRE DEUX CARACTERES QUANTITATIFS

En amont de toute mesure de corrélation à l'aide de coefficients appropriés, il est nécessaire de définir la forme d'une éventuelle relation entre deux caractères à l'aide d'une représentation graphique appropriée. En effet, selon la forme de la relation observée, on ne fera pas les mêmes hypothèses et on n'utilisera pas les mêmes outils de mesure.

Le diagramme de corrélation

Pour savoir s'il existe une relation entre deux caractères, on établit un diagramme de corrélation, c'est à dire un diagramme croisant les modalités de X et de Y. Chaque élément i est représenté par le point de coordonnées (X_i,Y_i). L'ensemble des points forme un nuage de points dont la forme permet de caractériser la relation à l'aide de trois critères :
 

- intensité de la relation
- forme de la relation
- sens de la relation
 
 

L'intensité de la relation

Une relation est forte si les unités ayant des valeurs voisines sur X ont également des valeurs voisines sur Y, c'est à dire si l'on a la relation suivante
 

Xi proche de Xj => Yi proche de Yj

=> le nuage de point prend alors la forme d'une ligne ou d'une courbe dont les points s'écartent peu.
 

Une relation est faible si les unités ayant des valeurs voisines sur X peuvent avoir des valeurs éloignées sur Y, c'est à dire si deux valeurs proches de X peuvent correspondre à deux valeurs très différentes de Y

=> le nuage de point n'a pas la forme d'une ligne ou d'une courbe, ou seulement de façon très grossière.
 

Une relation est nulle si les valeurs de X ne permettent aucunement de prédire les valeurs de Y

=> le nuage de point a le forme d'un carré, d'un cercle, d'une "patate" sans véritables lignes directrices.
 
 
 

absence de relation

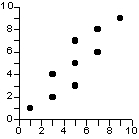
relation faible

relation forte

 
 

La forme de la relation

Une relation est linéaire si l'on peut trouver une relation entre X et Y de la forme Y=aX+b, c'est à dire si le nuage de point peut s'ajuster correctement à une droite.

Une relation est non-linéaire si la relation entre X et Y n'est pas de la forme Y=aX+b, mais de type différent (parabole, hyperbole, sinusoïde, etc). Le nuage de point présente alors une forme complexe avec des courbures.

Une relation non-linéaire est monotone si elle est strictement croissante ou strictement décroissante, c'est-à-dire si elle ne comporte pas de minima ou de maxima. Toutes les relations linéaires sont monotones.
 
 

relation non-linéaire et non-monotone

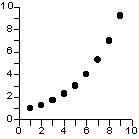
relation non-linéaire et monotone

relation linéaire (toujours monotone)

 

Le sens de la relation

Une relation monotone (linéaire ou non) est positive si les deux caractères varient dans le même sens, c'est à dire si l'on observe en général que :
 

Xi  > Xj => Yi > Yj

- les valeurs fortes de X correspondent généralement aux valeurs fortes de Y
- les valeurs moyennes de X correspondent généralement aux valeurs moyennes de Y
- les valeurs faibles de X correspondent généralement aux valeurs faibles de Y
 

Une relation monotone est négative si les deux caractères varient en sens inverse, c'est à dire si l'on observe en général que
 

Xi  > Xj => Yi < Yj

- les valeurs fortes de X correspondent généralement aux valeurs faibles de Y
- les valeurs moyennes de X correspondent généralement aux valeurs moyennes de Y
- les valeurs faibles de X correspondent généralement aux valeurs fortes de Y
 
 
 

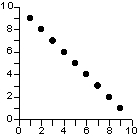
relation linéaire positive	relation linéaire négative
relation non-linéaire positive	relation non-linéaire négative

 
 
 

LE CALCUL DES COEFFICIENTS DE CORRELATION

Les coefficients de corrélation permettent de donner une mesure synthétique de l'intensité de la relation entre deux caractères et de son sens lorsque cette relation est monotone. Le coefficient de corrélation de Pearson permet d'analyser les relations linéaires et le coefficient de corrélation de Spearman les relations non-linéaires monotones. Il existe d'autres coefficients pour les relations non-linéaires et non-monotones, mais ils ne seront pas étudiés dans le cadre de ce cours.
 

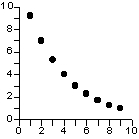
Pour illustrer l'usage de ces coefficients, on partira de l'exemple (fictif) d'une étude de psychosociobiologie visant à examiner s'il existe une relation entre la taille des pieds des enfants et leur intelligence. Partant d'un échantillon de 10 enfants (notés A, B, ...J) on examinera s'il existe une corrélation, linéaire ou non, entre la pointure de leurs chaussures (X) et leur quotient intellectuel (Y). Les données de l'analyse sont rassemblées dans le tableau 1, ci-dessous

Tableau 1 : Pointure des chaussures (X) et quotient intellectuel (Y) de 10 enfants d'âge scolaire
(données fictives)

enfant	X	Y
A	31	50
B	31	55
C	32	52
D	33	56
E	33	63
F	34	65
G	35	69
H	36	90
I	37	110
J	38	150
moyenne	34	76
écart-type	2.4	32

On se propose d'examiner s'il existe une relation entre la capacité à épeler et la taille des pieds : il y a quatre réponses possibles :

- plus la taille des pieds est importante, plus la capacité à épeler est importante (RELATION POSITIVE)
- plus la taille des pieds est importante, moins la capacité à épeler est important (RELATION NEGATIVE)
- la taille des pieds est liée au quotient intellectuel par une relation complexe comportant au moins un maximum et un minimum (RELATION NON MONOTONE)
- la taille des pieds n'est pas liée à la capacité à épeler (RELATION NULLE)
 
 
 
 

Le coefficient de corrélation linéaire de Bravais-Pearson

Ce coefficient permet de détecter la présence ou l'absence d'une relation linéaire entre deux caractères quantitatifs continus. Pour calculer ce coefficient il faut tout d'abord calculer la covariance. La covariance est la moyenne du produit des écarts à la moyenne.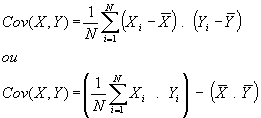
 
 

Le coefficient de corrélation linéaire de deux caractères X et Y est égal à la covariance de X et Y divisée par le produit des écarts-types de X et Y
 

Remarque : lorsque deux caractères sont standardisés, leur coefficient de corrélation est égal à leur covariance puisque leurs écarts-types sont égaux à 1.
 

Propriétés et interprétation de r(XY)
 

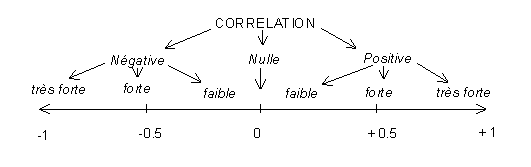
On peut démontrer que ce coefficient  varie entre -1 et +1. Son interprétation est la suivante :

- si r est proche de 0, il n'y a pas de relation linéaire entre X et Y
- si r est proche de -1, il existe une forte relation linéaire négative entre X et Y
- si r est proche de 1, il existe une forte relation linéaire positive entre X et Y

Le signe de r indique donc le sens de la relation tandis que lala valeur absolue de r  indique l'intensité de la relation c'est-à-dire la capacité à prédire les valeurs de Y en fonctions de celles de X.
 

Exemple : Calcul de la corrélation linéaire entre taille des pieds et intelligence de 10 enfants d'âge scolaire (Cf. tableau 1).
 

Tableau 2 : Exemple de calcul du coefficient de corrélation de Bravais-Pearson

enfant (i)	Xi	Yi	(Xi -mX)	(Yi -mY)	(Xi-mX)(Yi-mY)
A	31	50	-3	-26	78
B	31	55	-3	-21	63
C	32	52	-2	-24	48
D	33	56	-1	-20	20
E	33	63	-1	-13	13
F	34	65	0	-11	0
G	35	69	1	-7	-7
H	36	90	2	14	28
I	37	110	3	34	102
J	38	150	4	74	296
moyenne	34	76	0	0	64.1
écart-type	2.4	32

La covariance de X et Y étant égal à 64.1, on obtient le coefficient de corrélation de X et de Y en divisant la covariance par le produit de l'écart-type de X et de l'écart-type de Y :

r(X,Y) = 64.1 / (2.4 * 32) =  +0.83

Nous sommes en présence d'une corrélation positive forte, qui semble indiquer qu'il existe une relation linéaire (de type Y=aX+b) reliant le quotient intellectuel des enfants et la taille de leurs pieds. Toutefois, le coefficient de corrélation ne nous indique pas (1) si la relation observée est significative (fruit du hasard ou non) et (2) si elle correspond à une relation de cause à effet entre les deux facteurs X et Y étudiés. De plus, l'importance de la corrélation linéaire ne préjuge pas de l'existence d'un meilleur ajustement, qui serait quant à lui de type non-linéaire.

Limites du coefficient de Pearson

En principe, le coefficient de Pearson n'est applicable que pour mesurer la relation entre deux variables X et Y ayant une distribution de type gaussien et ne comportant pas de valeur exceptionnelles. Si ces conditions ne sont pas vérifiées (cas fréquent ...) l'emploi de ce coefficient peut aboutir à des conclusions erronées sur la présence ou l'absence d'une relation.

On notera également que l'absence d'une relation linéaire ne signifie pas l'absence de toute relation entre les deux caractères étudiés.
 

Le coefficient de corrélation de rang de Spearman.

Le coefficient de corrélation de rang (appelé coefficient de Spearman) examine s'il existe une relation entre le rang des observations pour deux caractères X et Y, ce qui permet de détecter l'existence de relations monotones (croissante ou décroissante), quelle que soit leur forme précise (linéaire, exponentiel, puissance, ...).  Ce coefficient est donc très utile lorsque l'analyse du nuage de point révèle une forme curviligne dans une relation qui semble mal s'ajuster à une droite. On notera également qu'il est préférable au coefficient de Pearson lorsque les distributions X et Y sont dissymétriques et/ou comportent des valeurs exceptionnelles.

Le coefficient de Spearman est fondé sur l'étude de la différence des rangs entre les attributs des individus pour les deux caractères X et Y :
 
 

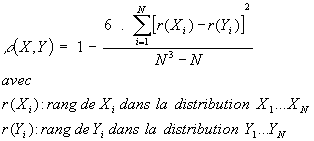Ce coefficient varie  entre -1 et +1. Son interprétation est la même que celui de Pearson, mais il permet de mettre en évidence des relations non-linéaires lorsqu'elles sont positives ou négatives.

Exemple : Calcul de la corrélation de rang  entre taille des pieds et intelligence de 10 enfants d'âge scolaire (Cf. tableau 1).

Tableau 3 : Exemple de calcul du coefficient de corrélation de Bravais-Pearson

enfant	X	Y	X'	Y'	(X'-Y')	(X'-Y')2
A	31	50	1.5	1	0.5	0.25
B	31	55	1.5	3	-1.5	2.25
C	32	52	3	2	1	1
D	33	56	4.5	4	0.5	0.25
E	33	63	4.5	5	-0.5	0.25
F	34	65	6	6	0	0
G	35	69	7	7	0	0
H	36	90	8	8	0	0
I	37	110	9	9	0	0
J	38	150	10	10	0	0
somme	340	760	55	55	0	4

La somme du carré des différences de rang étant égale à +4, et le nombre d'individus étudiés étant égal à 10, on en déduit la valeur du coefficient de corrélation de Spearman :

R =1- [(6*4)/(1000-10)] =+ 0.98

Le fait que la valeur du coefficient de Spearman soit positive confirme les résultats précédents (plus les enfants ont des grands pieds, plus leur quotient intellectuel est important). Mais le fait que la corrélation soit beaucoup plus forte en valeur absolue suggère l'existence d'une relation non-linéaire entre les deux variables. Cette hypothèse est confirmée par le diagramme de corrélation

 
 
 
 

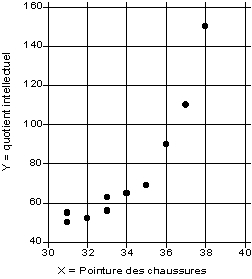
SIGNIFICATIVITE D'UNE RELATION

Le calcul d'un coefficient de corrélation ne constitue qu'une première étape dans l'analyse de la relation entre deux caractères. Il s'agit tout au plus d'une étape exploratoire qui doit être validée par un test de la significativité de la relation et par une vérification de la validité de la relation (absence de biais).
 

Test de la significativité d'une relation

Les coefficient de corrélation de Pearson ou de Spearman ne renseignent pas sur le degré de significativité d'une relation car celle-ci dépend également du nombre d'observation.
 

Exemple : on veut étudier le lien entre cancer et tabagisme.
- Un r de + 0.6 établi sur un échantillon de 10 personnes n'est pas significatif au seuil de 5%  (il peut s'agir d'un hasard).
- Un r de + 0.2 établi sur un échantillon de 200 personnes est  significatif au seuil de 5%  (la taille de l'échantillon fait que la relation, bien que faible  a peu de chances d'être due au hasard).

Pour déterminer si une relation est significative, il faut procéder à un test d'hypothèse en procédant de la façon suivante :

(1) H0 : il n'y a pas de relation entre les deux caractères X et Y
(2) On se fixe un risque d'erreur pour le rejet de H0 (exemple alpha=5%)
(3) On calcule la valeur absolue du coefficient de corrélation r(X,Y) dans la table correspondante (Pearson ou Spearman)
(4) On calcule la valeur théorique r(alpha, N.) de ce coefficient qui n'est dépassé que dans alpha % des cas
(5) On teste H0 vraie si r(alpha, d.d.l.) > abs[ r(X,Y) ]
(6) On accepte ou rejette H0

Exemple : Pour 10 observations, les valeurs critiques du coefficient de Spearman sont 0.564 au seuil de 5% et 0.746 au seuil de 1%. La valeur observée étant de +0.98, on peut rejeter H0 et affirmer avec moins de 1% de chances de se tromper que la relation observée entre la taille des pieds et le quotient intellectuel des enfants n'est pas le fruit du hasard.
 

Vérification de l'absence de biais

Le fait que le test de significativité permette de rejeter l'hypothèse d'indépendance ne doit pas amener à conclure trop vite à l'existence d'une relation. Celle-ci peut souvent être la conséquence de biais liés à un mauvais respect des conditions d'utilisation des coefficients de corrélation. Quelques exemples fréquents de corrélation biaisée sont indiquées ci-dessous.
 
 

Conclusion erronée sur l'absence de relation

Dans l'exemple présenté ci-dessus les deux coefficients de corrélation (Pearson, Spearman) sont nuls, mais pourtant il existe bel et bien une relation (non-linéaire et non-monotone) entre les deux variables X et Y. Un simple examen des coefficients sans avoir tracé le nuage de points ferait manquer un résultat essentiel.

Influence d'une valeur exceptionnelle

 

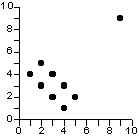
Dans l'exemple présenté ci-dessus, le calcul du coefficient de corrélation de Pearson aboutirait à l'idée qu'il existe une corrélation positive (+0.54) mais non significative (au seuil de 5%) entre les deux variables. Or, cette corrélation positive résulte uniquement de l'influence du point exceptionnel (9,9). Si l'on retire ce dernier, on obtient une corrélation négative (-0.67) et significative (au seuil de 5%) entre les deux variables, soit une conclusion doublement inverse de la précédente !

Emboîtement de relations et composante d'échelle

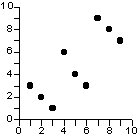
Dans l'exemple ci-dessus il n'est pas faux de conclure à l'existence d'une relation positive significative (+0.75) mais celle-ci est le résultat des différences de comportement de trois sous-population à l'intérieur desquelles la relation est au contraire rigoureusement négative. Il existe donc une composante d'échelle dans la relation observée et les conclusions seront très variable selon l'échantillon considéré.

Une astuce utile : la comparaison des coefficients de Pearson et Spearman

La plupart des biais peuvent être assez facilement détectés à travers l'analyse du nuage de point. Malheureusement cette méthode n'est pas applicable lorsque l'on veut calculer les corrélations entre de nombreuses variables prises 2 à 2.

Dans ce cas, un truc utile consiste à calculer systématiquement les deux coefficients de corrélation (Pearson et Spearman) et à vérifier s'ils donnent des résultats conformes. Si ce n'est pas le cas, c'est probablement qu'il y a anguille sous-roche ...

signif(Pearson) > signif(Spearman) : ceci indique fréquemment la présence de valeurs exceptionnelles qui augmentent la valeur du coefficient de Pearson mais ne modifient pas celle du coefficient de Spearman, beaucoup plus robuste.

signif(Spearman) > signif(Pearson) : ceci indique fréquemment l'existence d'une relation non-linéaire, mieux prise en compte par le coefficient de Spearman que par celui de Pearson.

Evidemment, il y a toujours des cas vicieux où les deux coefficients donnent le même résultat et où pourtant la relation est biaisée...
 

CORRELATION ET CAUSALITE

UNE CORRELATION N'IMPLIQUE PAS NECESSAIREMENT UNE CAUSALITE !!!!
 
 
 

Quelques familles d'explications d'une corrélation

 

 
 
 

Exemple : Analphabétisme des femmes (TAN) et mortalité des garçons avant 5 ans en Afrique (TMO).
 

* Causalité directe :
TAN => TMO : Les femmes qui ne savent pas lire ne peuvent pas soigner les enfants car elles n'ont pas lu Freud, Brazelton et Laurence Pernoud.
TMO => TAN : La mortalité des jeunes enfants désespère les femmes qui renoncent à lire Freud, Brazelton et Laurence Pernoud.
 

* Chaînes causales linéaires :
En réalité, les deux exemples ci-dessus correspondent moins à des causalité directe qu'à des chaînes causales :
TAN => lecture impossible => Pas d'information sur Freud => Enfant mal soigné => TMO

* Chaînes causales arborescente :
L'un des caractères peut n'être qu'un facteur parmi d'autre qui influence le second :
TAN                         => TMO
Malnutrition                 => TMO
Climat                         => TMO
Sous-médicalisation     =>TMO
 
 

* Présence d'une cause commune :
sous-développement => TMO
                                => TAN

* Présence de causalités circulaires (boucles de rétroaction)
sous-développement  <=> TAN
 

* Finalement, le cas général est l'existence d'un système causal au sein duquel sont placés les deux caractères étudiés. La découverte d'une corrélation ne permet pas de conclure à l'existence d'une relation de cause à effet mais doit inciter à construire un système causal rendant compte de la corrélation observée
 
 

Corrélation et prédiction : le paradoxe de la Grenouille d'Albert Simon.

Bien que cela soit plutôt humiliant pour l'esprit, il n'est pas toujours nécéssaire de comprendre pour agir. Supposons que l'on observe une corrélation de +0.98 entre le comportement de la grenouille d'Albert Simon sur son échelle et le temps du lendemain. On peut chercher quel système causal rend compte de la liaison observée entre le comportement de la bestiole et le temps (hygrométrie, pression, etc). Mais ignorerions nous tout ceci, nous ne pourrions pas moins prévoir le temps avec une bonne certitude si la corrélation est effectivement de +0.98.
 

Tous les proverbes du type "Noël au balcon, Pâques au tisons" ou "Noël au scanner, Pâques au cimetierre" (P. Desproges) sont des corrélations empiriques qui ne sont pas toujours explicables mais qui peuvent être utiles pour la prévision si elles s'avèrent fortes.
 

Un danger spécifique à la géographie : l'erreur écologique.

En géographie, l'étude des corrélations se fait souvent à travers l'analyse d'un ensemble de lieux. Lorsque les variables décrivant ces lieux sont des attributs sociaux décrivant les habitants il faut toujours faire attention au fait qu'une corrélation établie au niveau des lieux n'implique pas forcément une corrélation au niveau des individus.
 

Exemple : Criminalité et étrangers à Trifouilly.
 

=> l'étude menée au niveau des individus (sociologique) montre que le taux de criminalité est plus élevé chez les autochtones (36%) que chez les étrangers (17%).
=> pourtant, l'étude menée au niveau des quartiers (géographique) montre une corrélation parfaite (+1) entre la proportion d'étrangers des quartiers et leur taux de criminalité.
 

Il n'y a aucun paradoxe : la présence d'une corrélation au niveau des lieux signifie simplement que là où il y a beaucoup d'étrangers il y à aussi beaucoup de criminels, mais elle ne prouve pas que les étrangers soient la cause de la criminalité.

Ce type d'erreur est appelé erreur écologique car elle consiste à penser que la présence de deux phénomènes au même endroit (écosystème) implique l'existence d'une relation causale entre ces deux phénomènes.
 
 

 

Menu général

Chapitre précédent

Chapitre suivant