Chapitre 1 : INTRODUCTION GENERALE - DEFINITIONS

1.1) DEFINITION DE LA STATISTIQUE

1.2) COLLECTE DE L'INFORMATION

1.3) TYPES DE CARACTERES
 
 

Menu général

Chapitre suivant

 

Qu'elle soit définie comme l'angle spatiale des sciences sociales, l'analyse des relations entre l'homme et la nature ou l'étude de la surface de la terre, la géographie est perpetuellement confrontée au nombre et à la mesure. Quel que soit l'angle d'étude choisi, le point de départ de la géographie est toujours la localisation et la mesure d'une catégorie de phénomènes sociaux dans l'espace.

La statistique est au géographe ce que la pratique des langues étrangères est au diplomate : ce n'est pas l'objet même de la discipline mais c'est un outil indispensable sans lequel on se trouve gravement handicapé. De même qu'un diplomate ignorant des langues étrangères peut faire appel à un interprète, le géographe ignorant de la statistique peut faire appel à un spécialiste du traitement des données. Mais dans l'un et l'autre cas, la présence d'un intermédiaire risque de réduire l'efficacité voire d'introduire des erreurs : erreurs de traduction pour l'interprète qui ne maîtrise pas la complexité d'une situation diplomatique, erreur d'interprétation pour le statisticien qui ne connaît pas précisément la problématique du géographe.

La géographie est plus que la mesure mais il n'y a pas de géographie sans mesure.
 

1.1) DEFINITION DE LA STATISTIQUE

Le terme statistique désigne à la fois :

1) l'ensemble des données numériques concernant une catégorie de faits (sens très ancien). Le mot a été introduit à l'origine pour caractériser les études méthodiques des faits sociaux par des procédés numériques destinés à renseigner et aides les gouvernants (classements, recensements, dénombrements, inventaires).Il s'agit de l'expression dans sa signification la plus usuelle :

- "la statistique du chômage en 1990"
- "la statistique des investissements japonais en France"

2) l'ensemble des méthodes mathématiques permettant :

a) de résumer quantitativement l'information recueillie sur un ensemble d'éléments au moyen d'une investigation exhaustive. C'est la statistique descriptive, qui fait l'objet de ce cours.

b) de généraliser à de grands ensembles d'éléments les conclusions tirées des résultats obtenus avec des ensembles beaucoup plus restreints appelés échantillons. C'est la statistique inférentielle ou probabiliste, qui n'est pas abordée dans ce cours.
 

1.2) COLLECTE DE L'INFORMATION

 
Le tableau élémentaire

Toute collecte de données commence par la définition de l'ensemble observé et par l'établissement de la liste de ses éléments. Quand on construit le tableau, chaque élément est inscrit progressivement sur une des lignes de ce qui va devenir le tableau élémentaire des données. C'est un tableau à simple entrée où les lignes correspondent aux éléments étudiés et les colonnes aux caractères (ou variables) décrivant ces éléments. La première colonne est en principe réservée à un identificateur permettant de différencier les éléments.
 
 
 
 

N°	Identificateur	Caractère
1
2
...
i
...
N

L'ensemble observé

C'est la collection, le plus souvent finie en géographie, d'unités (ou d'éléments ou d'individus) sur laquelle vont porter nos observations. Cette collection constitue l'ensemble observé. Pour que l'ensemble soit bien défini, il faut que, pour chaque unité (ou élément ou individu), on puisse répondre par oui ou par non à la question : l'unité (ou l'élément, ou l'individu) est-il élément de l'ensemble observé ?

En géographie, l'ensemble observé est dans la plupart des cas un ensemble d'unités spatiales, c'est à dire d'éléments très précisément localisés à la surface de la terre, et donc susceptibles d'être cartographiés. Ceci explique le lien entre les enseignements de statistique et de cartographie dans le cadre de cet enseignement.

On peut distinguer trois grands types d'unités spatiales :

• les unités de type aréal ou zonal (départements, régions, Etats, affleurement géologique, zone climatique ...)
•  les unités de type ponctuel (villes, établissements industriels, points géodésiques, volcan, station météorologique, ... ).
•  les unités de type linéaire (rue, tronçon ferroviaire, ligne de faille, front climatique, etc).

Le titre du tableau élémentaire doit définir l'ensemble étudié avec un libellé très précis qui ne comporte aucune ambiguité (i.e. deux personnes utilisant la même définition doivent aboutir à la même liste d'éléments).

Exemple :
"Les Etats africains représentés à l'ONU  en 1980" est précis alors que
"Les pays africains" est ambïgu et peu clair.

L'ensemble étudié sera désigné par E.

L'élément (ou individu)
 

C'est l'un des objets constitutifs de l'ensemble observé. Nous appellerons n le nombre d'éléments de l'ensemble E. Chaque élément de l'ensemble E aura son propre identificateur (nom, code) mais pourra être également désigné par sa position dans la liste des éléments, notée à l'aide d'un indice i dont la valeur est comprise entre 1 et n.

Le caractère

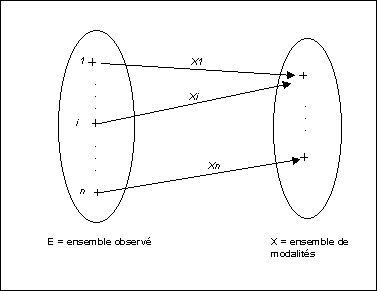
En fonction de la question posée, les éléments de l'ensemble observé sont décrits ou caractérisés par un ou plusieurs caractères. Définir un caractère revient à établir une correspondance entre chaque élément i de l'ensemble E (appelé ensemble de départ de l'application) et un é lément et un seul, noté  x_i d'un ensemble X (dit ensemble d'arrivée de l'application).
 

 
 

Exemple : E = Les Etats et territoires Americains avec E = { Honduras, Belize, Brésil, ...}

X = Statut politique en 1989 avec X = { "dépendant"; "indépendant"}

Pour chaque élément de E on peut établir une application dans l'ensemble du caractère Statut Politique
 

Modalités d'un caractère

Les situations où les éléments peuvent se trouver à l'égard du caractère considéré sont les différentes modalités de ce caractère. Attention, les modalités sont les valeurs possibles et pas uniquement les valeurs effectivement observés. Ainsi, 3 333 333 hab. est une modalité possible du caractère population, même si aucun élément de l'ensemble observé ne prend cette valeur.
 

Les modalités d'un caractères doivent être à la fois :
 

•  incompatibles : un élément ne doit pas correspondre à plus d'une seule modalité d'un caractère.
• exhaustives : chaque élément de l'ensemble observé doit recevoir une modalité du caractère considéré.

Exemple : si l'ensemble observé est l'ensemble des rues du XIIIe arrondissement.

•  le caractère "Type de circulation automobile" (rues à sens unique, rue à double sens, rues en impasse) a des modalités qui ne sont pas incompatibles car une rue peut être à la fois en double sens et en impasse (ce qui vaut mieux ... car sinon comment en sortir ?).

•  le caractère "Type de circulation automobile" (rues à sens unique, rue à double sens) a des modalités qui ne sont pas exhaustives car certaines rues peuvent être interdites à la circulation et ne sont donc ni à double sens, ni à sens unique (ex. la rue Student est une rue piétonnière)

• le caractère est correctement défini si on lui donne les trois modalités ("double sens", "sens unique", "autres cas") qui sont à la fois incompatibles et exhaustives. Il vaut mieux utiliser "autres cas" que "circulation interdite" car il peut toujours subsister des cas particuliers et imprévus (rue en travaux, circulation possible uniquement à certaines heures, etc.).

1.3) TYPES DE CARACTERES

On distingue deux grandes familles de caractères : les caractères qualitatifs et les caractères quantitatifs. Un critère commode est le suivant : la moyenne d'un caractère quantitatif a un sens alors que la moyenne d'un caractère qualitatif est impossible à réaliser ou bien n'a aucune signification.

Caractère qualitatif

Un caractère est qualitatif si la moyenne de ses modalités est impossible (caractère nominal) ou triviale (caractère ordinal).
 
•  échelle nominale : chaque modalité est exprimée par un nom ou un code. Les différentes modalités ne sont pas ordonnables.
•  échelle ordinale : chaque modalité est explicitement significative du rang pris par chaque individu pour le caractère considéré. Si E possède N éléments, les modalités seront 1er, 2eme, 3eme, ...Neme. Comme on possède juste l'ordre des individus, on ne sait rien de l'intervalle des valeurs. Le calcul d'une moyenne est absurde. Il s'agit bien d'un caractère qualitatif.

Caractère quantitatif

Un caractère est quantitatif si ses modalités s'expriment par des nombres (condition nécéssaire mais pas suffisante), et si la moyenne de ces nombres a un sens.

repérable ou mesurable

On distingue les caractères quantitatif s repérables sur une échelle d'intervalle et les caractères quantitatifs mesurables selon que la valeur 0 est arbitraire ou selon qu'elle a un sens concret.

•  quantitatif repérable sur une échelle d'intervalle. Ces caractères permettent de repérer la position de chaque individu par rapport àune origine arbitraire. La valeur 0 est donc conventionnelle et ne signifie pas l'absence du phénomène. (Ex. : Latitude, longitude, température, altitude, ...)
• quantitatif mesurable sur une échelle numérique . Le 0 signifie bien l'absence du phénomène (Ex. : population, taux de fécondité, précipitations)

stock ou intensité

On peut par ailleurs distinguer les caractères quantitatifs de stock et les caractères quantitatifs d'intensité (taux) selon que la somme des modalités a un sens ou non. .

• les caractères quantitatifs de stock expriment des quantités concrètes : la somme des modalités des éléments a un sens.( Ex. La population est un caractère de stock car la somme de plusieurs populations a un sens)
• les caractères quantitatifs d'intensité expriment des caractéristiques des individus mais leur total n'a pas de signification. (Ex. la densité de population est un caractère de rapport car la somme de plusieurs densités de population n'a aucun sens)

Remarque : le fait qu'un caractère soit exprimé en % ne signifie pas qu'il s'agit d'un taux. En effet, si les départements français sont décrits par leur part de la population française (en %), le total a un sens (100 %) et il s'agit donc d'un stock exprimé en % du total.
 

discret ou continu

Enfin, on peut distinguer les caractères quantitatifs discrets et les caractères quantitatifs continus selon que leurs modalités sont définies sur un intervalle continu de l'ensemble des réels (modalités en nombre infini) ou selon qu'elles correspondent à un ensemble fini et dénombrable de valeurs entières ou réelles.
 

• les caractères quantitatifs discrets sont des caractères dont les modalités sont des nombres isolés, pas nécessairement entiers. (Ex. Soit le caractère prix décrivant un ensemble E de N oranges. La marchande peut choisir de classer ces oranges en trois classes (grosses, moyennes, petites) qui sont vendues respectivement 1.50 F, 1.10 F et 0.75 F. Le caractère "prix" est discret et prend trois modalités qui ne sont pas des entiers)

•  les caractères quantitatifs continus sont des caractères dont les modalités sont définies sur un intervalle (continu) de valeur donné appelé domaine de variation et défini par les valeurs Xmin et Xmax. (Ex. Si la marchande décide de vendre ses oranges au poids, mettons 10 F le kilog, il y a une infinité de modalités possibles pour le caractère prix d'une orange. Si le poids minimum d'une orange est 50 g et le poids maximum 250 g, les modalités du caractère "prix d'une orange" sont définies sur l'intervalle [0.5F; 2.5 F])

• Il faut toutefois observer que certains caractères discrets peuvent être assimilés à des caractères continus lorsqu'ils prennent un très grand nombre de modalités (Ex. la population des départements français est un caractère discret puisque les modalités sont des nombres isolés : on peut avoir 253334 h ou 253335 h mais pas 253334.5 h. Dans la pratique, on pourra appliquer à ce caractère des traitements statistiques qui sont en principe réservés aux caractères continus).

combinaisons de critères
 

Les typologies précédentes  se combinent lorsque l'on veut définir le type d' un caractère quantitatif :

• le caractère densité de population est un caractère quantitatif, mesurable, de rapport, continu.
•  le caractère population est un caractère quantitatif, mesurable, de stock, discret (mais assimilable dans certains cas à un caractère continu).

Il est très important de savoir définir le type d'un caractère car les outils statistiques ou les représentations graphiques ne sont pas les mêmes selon le type de caractère à étudier. Par exemple, l'étude de la relation entre deux caractères discrets se fait à l'aide d'un tableau de contingence  alors que la mise en relation de deux caractères quantitatifs continus se fait à l'aide de la corrélation et de la régression  et que la relation entre un caractère qualitatif et un caractère quantitatif se fait à l'aide de tests (Student) ou par décomposition de la variance (Fischer).
 
 

Menu général

Chapitre suivant