AGREGATION DE GEOGRAPHIE
Préparation à l'épreuve écrite de commentaire de documents

Claude Grasland
Université Paris VII / UFR GHSS / Année 2001-2002 

Module n°6
ANALYSE D'UNE MATRICE DE FLUX
(Les modèles d'interaction spatiale)

Cours  Exercices  Bibliographie  Menu précédent

Cours

Objectifs
 

1- Apprendre à décrire une matrice de flux (soldes, volumes, échanges, flux dominants) et à cartographier les éléments les plus significatifs.
2- Repérer les principaux facteurs explicatifs des flux (Emission, Reception, Proximité spatiale ou territoriale)
3- Savoir interpréter les résidus d'un modèle d'interaction spatiale
 

A. LA DESCRIPTION D'UNE MATRICE DE FLUX

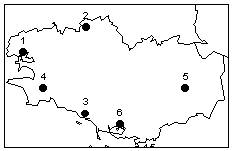
On partira d'un exemple très simple ne comportant que 6 lieux, pour mettre en évidence les différentes étapes de description d'une matrice de flux.
 

A partir d'une enquête effectuée par la Direction des Etudes et de la Prospective (DEP) du ministère de l'Education Nationale et de l'Enseignement Supérieur (MESR), on peut connaître l'évolution de la localisation des étudiants français du supérieur entre les rentrées de 1993 et 1994. Même si cette localisation est connue avec une certaine incertitude (un étudiant peut être inscrit à l'Université de Rennes mais suivre les cours dans une antenne universitaire située dans une autre ville de Bretagne), l'enquête permet de reconstituer assez bien les déplacements des étudiants entre les villes françaises au cours de la période 1993-1994, surtout si on se limite aux plus grandes d'entre elles.
 
 
n° Ville Population de l'agglomération en 1991

(en hab.)
1
 BREST 
201 000
2
 LANNION 
20 000
3
 LORIENT 
115 000
4
 QUIMPER 
66 000
5
 RENNES 
245 000
6
 VANNES 
46 000


 
vers (j)
Fij
BRE
LAN
LOR
QUI
REN
VAN
Oi
BRE
-
19
10
54
369
14
466
LAN
40
-
4
0
48
6
98
de
LOR
19
0
-
2
6
2
29
(i)
QUI
67
0
0
-
29
9
105
REN
190
62
5
21
-
70
348
VAN
8
1
0
0
56
-
65
Dj
324
82
19
77
508
101
1111

A.1 Analyse des marges (solde, volume)

La première étape de l'analyse consiste à étudier les marges de la matrice (sommes en ligne ou sommes en colonnes) pour en déduire un certain nombre d'indicateurs de base sur les lieux.
 
i Ville Départs Arrivées Volume Solde Attractiv.
(O) (D) V=(O+D) S=(D-O) A=(S/V)
1
 BREST 
466
324
790
-142
-18%
2
 LANNION 
98
82
180
-16
-9%
3
 LORIENT 
29
19
48
-10
-21%
4
 QUIMPER 
105
77
182
-28
-15%
5
 RENNES 
348
508
856
160
19%
6
 VANNES 
65
101
166
36
22%

Une manière simple et efficace de résumer l'information consiste à combiner sur une seule carte le volume migratoire (taille) et l'indice d'attractivité (rapport solde/volume). On peut alors reprérer les pôles les plus importants (Rennes, Brest) et distinguer les centres attractifs (Rennes, Vannes) ou répulsifs (Brest, Lorient).

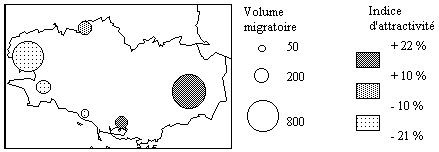
A.2 Analyse des origines-destinations (solde, volume)

Pour cartographier les flux, il est nécessaire de se fixer un seuil assez restrictif faute de quoi la carte sera difficilement lisible. L'utilisation de seuils (classes de flux) est parfois préférable aux variations proportionnelles.

Cartographie des 10 principaux flux migratoires

 

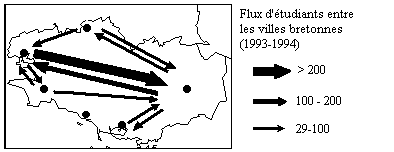
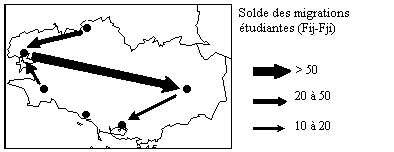
Il est toutefois préférable d'établir deux cartes séparées, l'une qui représente le volume des flux (F+) et l'autre qui représente le solde des flux (F-) pour chaque couple d'origine-destination. On peut ainsi mieux repérer les composantes symétriques et dissymétriques de l'échange.
 
F+ BRE LAN LOR QUI REN VAN Tot
BRE
0
59
29
121
559
22
790
LAN
59
0
4
0
110
7
180
LOR
29
4
0
2
11
2
48
QUI
121
0
2
0
50
9
182
REN
559
110
11
50
0
126
856
VAN
22
7
2
9
126
0
166
Tot
790
180
48
182
856
166
2222
F- BRE LAN LOR QUI REN VAN Tot
BRE
0
-21
-9
-13
179
6
142
LAN
21
0
4
0
-14
5
16
LOR
9
-4
0
2
1
2
10
QUI
13
0
-2
0
8
9
28
REN
-179
14
-1
-8
0
14
-160
VAN
-6
-5
-2
-9
-14
0
-36
Tot
-142
-16
-10
-28
160
36
0


 

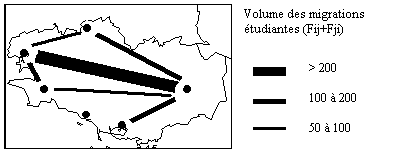
A.3 Analyse des flux dominants

Dans une autre optique, on peut établir des profils d'émigration et des profils d'immigration en divisant chaque ligne ou colonne par son total. Ceci permet de mieux repérer les spécificités de chaque lieu et les dissymétries liées aux différences de tailles.

Profils d'émigration
Fij/Oi BRE LAN LOR QUI REN VAN tot
BRE
0%
4%
2%
12%
79%
3%
100%
LAN
41%
0%
4%
0%
49%
6%
100%
LOR
66%
0%
0%
7%
21%
7%
100%
QUI
64%
0%
0%
0%
28%
9%
100%
REN
55%
18%
1%
6%
0%
20%
100%
VAN
12%
2%
0%
0%
86%
0%
100%

Profils d'immigration
Fij/Dj BRE LAN LOR QUI REN VAN
BRE
0%
23%
53%
70%
73%
14%
LAN
12%
0%
21%
0%
9%
6%
LOR
6%
0%
0%
3%
1%
2%
QUI
21%
0%
0%
0%
6%
9%
REN
59%
76%
26%
27%
0%
69%
VAN
2%
1%
0%
0%
11%
0%
tot
100%
100%
100%
100%
100%
100%

Une façon astucieuse de mettre en évidence la hiérarchie migratoire des centres consiste à utiliser la méthode des flux dominants proposée par Nyusten & Dacey ou une variante de celle-ci.
 

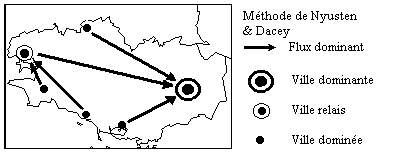
METHODE NYUSTEN & DACEY : i est dominé par j si :
(1) i envoie son flux le plus important vers j
(2) La somme des arrivées de j est plus importante que la somme des arrivées de i

VARIANTE DE LA METHODE NYUSTEN & DACEY : i est dominé par j si :
(1) i envoie k % de ses migrants vers j
(2) La somme des arrivées de j est plus importante que la somme des arrivées de i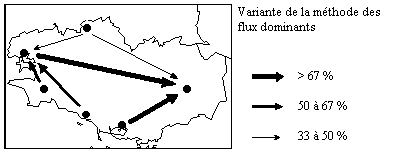
 

B. LES MODELES D'INTERACTION SPATIALE

Il est impossible de résumer ce chapitre fondamental de la géographie en quelques lignes. On rappellera donc juste quelques éléments historiques sur la mise en place du modèle gravitaire :
 

B.1) FIN XIXe : LES LOIS DE RAVENSTEIN
 
 
(Ravenstein E., 1885 & 1889, "The Laws of Migration", Journal of Royal Statist. Society, London)
  1. Le nombre de migrants diminue quand la distance augmente; la plupart ne vont pas très loin ; ceux qui se déplacent sur de grandes distances se dirigent de préférence vers les grands centres commerciaux et industriels.
  2. Le processus se fait de la façon suivante : une ville à croissance rapide attire les gens des régions environnantes ; les vides ainsi créés sont comblés par les migrants de districts plus éloignés ; la force d'attraction des grandes villes dynamiques se fait donc sentir de proche en proche en diminuant d'intensité. Le nombre de migrants de la zone d'accueil est donc proportionnel à la population de la zone d'origine et inversement proportionnel à la distance qui les sépare.
  3. Chaque courant principal de migration suscite un contre-courant compensatoire.
  4. Les citadins ont une mobilité plus faible que les ruraux
  5. Les femmes ont une mobilité plus forte que les hommes, au moins à courte distance.
  6. L'intensité des migrations augmente avec le développement du commerce, de l'industrie et des transports.
  7. Les facteurs déterminant la migration sont nombreux mais le plus important est le facteur économique
D'après Noin D., 1988, Géographie de la Population, Masson, Paris, pp. 273-274

B.2) DEBUT XXe : L'ANALOGIE GRAVITAIRE (PARETO, STEWART)

Sous des formes voisines, plusieurs auteurs proposent de transposer aux migrations humaines la loi de la gravitation universelle de Newtown :
 
Modèle de Newtown

Aij = g . Mi . Mj / Dij 2

Aij : force d'attraction entre i et j
g : constante gravitaire universelle
Mi, Mj : masse des planètes
Dij : distance entre les planètes

 Modèle de Stewart

Fij = k . Pi . Pj / Dij 2

Fij : nombre de migrants de i vers j
k : niveau global de mobilité
Pi, Pj : population des lieux i et j
Dij : distance entre les lieux i et

Les auteurs suivants introduisent des modification et proposent plusieurs variantes
 

Fij = k . (Pi)b1 . (Pj)b2 . (Dij) -a: modèle gravitaire généralisé (Paréto)
Fij = k . (Pi)b1 . (Pj)b2 . exp -a Dij : modèle gravitaire généralisé (exponentiel)
Fij = ai.Oi. bj. Dj. -a Tij : modèle entropique de Wilson
Fij = (Ai+Bj)/Dij : modèle additif de Tobler
 

B.3)  FIN XXe : LA REMISE EN CAUSE DE L'ANALOGIE GRAVITAIRE

De nombreux auteurs n'acceptent pas la transposition au comportement humain des lois de la physique et tentent d'expliquer autrement la décroissance des interactions avec la distance :
 
  • L'explication économique (ZIPF) : L'effet de la distance doit s'interpréter comme l'ajustement de l'offre et de la demande de mobilité en fonction du coût de déplacement. La distance n'agit que si elle est proportionnelle au coût de mise en relation. Les acteurs obéissent au principe du moindre effort (rationalité économique).
  • L'explication sociologique (S. STOUFFER) : Plus la distance augmente, plus le nombre d'occasions interposées (intervening opportunities) est élevé. Ce n'est donc pas la distance qui agit directement mais la population du fait que le migrant trouve d'autres occasions de migrer entre son lieu de départ et son lieu d'arrivée.
  • L'explication psychologique (T. HAGERSTRAND) : Toute migration est précédée d'un flux d'information (connaissance du lieu de destination). La décroissance des migrations avec la distance est liée à l'ignorance des migrants sur les lieux de destination éloignés.

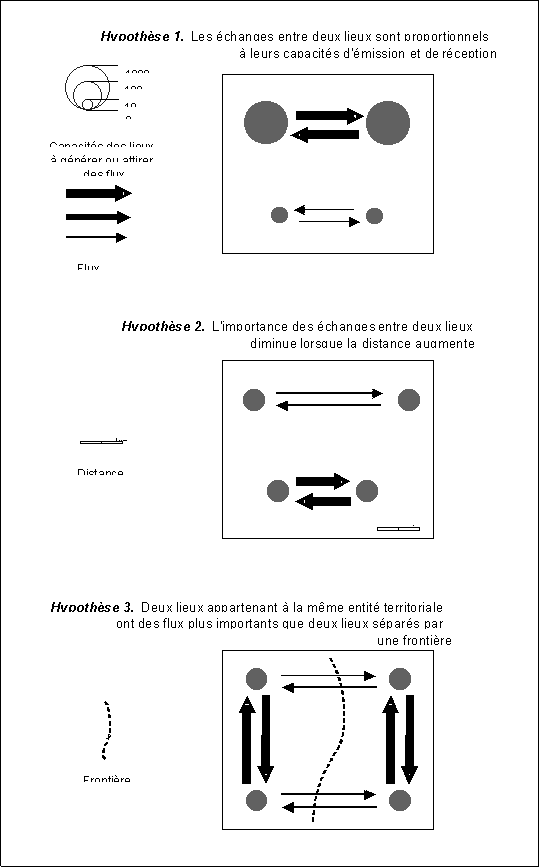
B.4) TROIS HYPOTHESES A RETENIR POUR LE COMMENTAIRE DE DOCUMENT.

Même si l'on n'est pas capable de maîtriser toutes les subtilités théoriques du modèle gravitaire, il faut toujours garder présentes à l'esprit les trois hypothèses suivantes lorsque l'on cherche à rendre compte des différences de flux entre les lieux. Un bon commentaire de document devra toujours examiner dans quelle mesure elles sont vérifiées et se combinent entre elles.


 

C. L'ANALYSE DES RESIDUS D'UN MODELE D'INTERACTION SPATIALE

S'il est exclu de demander à un candidat à l'agrégation de procéder à l'ajustement d'un modèle gravitaire, il est en revanche tout à fait possible que le jury lui propose de commenter les résidus d'un modèle gravitaire dont les paramètres ont été calculés (flux observés, flux théoriques, flux résiduels). Considérons par exemple les documents suivants :

(A) Description des données

Carte 1 : Organisation administrative de la Tchécoslovaquie en 1989

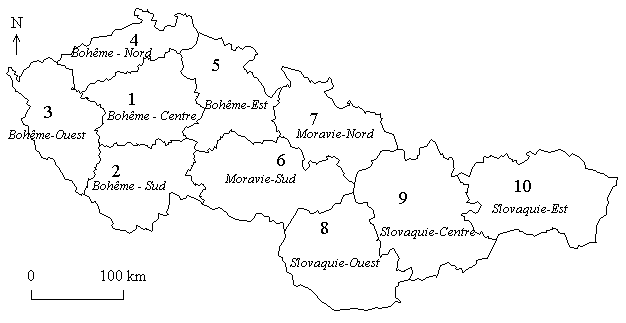
Tableau 1 : Population des régions de Tchécoslovaquie en 1989
 
i Code Région République
Population
1 BC Bohême-Centre Tchèque
2 333 670
2 BS Bohême-Sud Tchèque
698 568
3 BO Bohême-Ouest Tchèque
869 445
4 BN Bohême-Nord Tchèque
1 190 781
5 BE Bohême-Est Tchèque
1 239 979
6 MS Moravie-Sud Tchèque
2 058 234
7 MN Moravie-Nord Tchèque
1 971 580
8 SO Slovaquie-Ouest Slovaque
2 164 548
9 SC Slovaquie-Centre Slovaque
1 611 930
10 SE Slovaquie-Est Slovaque
1 499 708
    Tchécoslovaquie  
15638443

Tableau 2 : Migrations inter-régionales de population en Tchécoslovaquie en 1989
 
            vers            
    BC BS BO BN BE MS MN SO SC SE Total
  BC  
2096
1792
3025
2411
1110
793
395
284
282
12188
  BS
2420
  
756
543
360
853
348
153
91
106
5630
  BO
2635
1081
  
1312
399
553
369
213
211
146
6919
  BN
4120
1073
1542
  
1406
648
535
220
183
292
10019
de BE
3530
610
471
1275
  
1210
781
211
141
122
8351
  MS
2187
1337
669
702
1267
  
2643
707
338
239
10089
  MN
1852
593
662
682
1017
3143
  
599
623
370
9541
  SO
668
177
249
225
226
737
559
  
3126
732
6699
  SC
524
168
266
251
188
396
801
3839
  
1229
7662
  SE
769
206
292
534
302
444
689
1567
1487
  
6290
Total
18705
7341
6699
8549
7576
9094
7518
7904
6484
3518
83388

Carte 2 : Principaux flux migratoires entre les régions tchécoslovaques en 1989


 
 
 
 

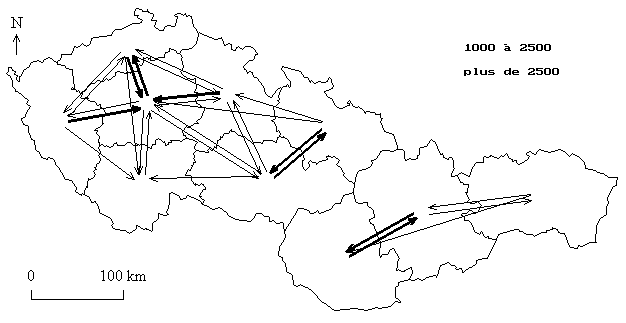
(B) Mise en évidence de la relation entre intensité des flux et distance

(a) Graphique arithmétique (b) Graphique bi-logarithmique


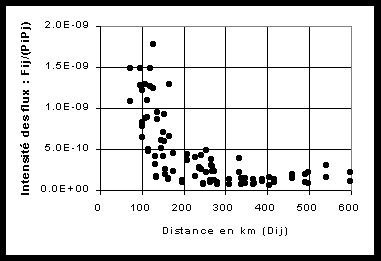
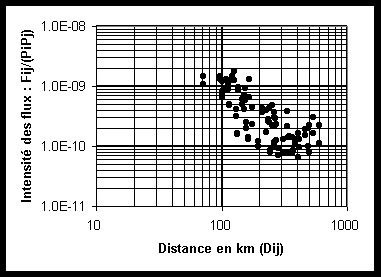
On remarque que l'intensité des flux est une fonction non-linéaire de la distance. Une modélisation permet de montrer que les flux (Fij) dépendent de la population de la région d'origine (Pi), de la population de la région d'arrivée (Pj) et de la distance entre ces deux régions (Dij) :

Fij = 3.34 . 10-7 . Pi . Pj . Dij -1.31

(C) Calcul des flux théoriques et des flux résiduels

Tableau 3 : Migrations estimées par le modèle gravitaire
 
F*ij BC BS BO BN BE MS MN SO SC SE Total
BC  
1389
1498
3548
2344
1874
1279
944
560
347
13782
BS
1389
  
366
352
413
668
355
345
179
106
4172
BO
1498
366
  
662
335
407
290
260
154
102
4075
BN
3548
352
662
  
806
649
529
378
241
159
7327
BE
2344
413
335
806
  
1725
1396
673
422
243
8357
MS
1874
668
407
649
1725
  
3250
2479
1120
512
12685
MN
1279
355
290
529
1396
3250
  
1840
1450
646
11034
SO
944
345
260
378
673
2479
1840
  
2415
778
10112
SC
560
179
154
241
422
1120
1450
2415
  
1205
7747
SE
347
106
102
159
243
512
646
778
1205
  
4097
Total
13782
4172
4075
7327
8357
12685
11034
10112
7747
4097
83388

On peut alors calculer la matrice des résidus du modèle d'interaction spatiale en effectuant la différence entre flux observés et flux théoriques : Rij=Fij-F*ij

Tableau 4 : Résidus des migrations estimées par le modèle gravitaire
 
Rij BC BS BO BN BE MS MN SO SC SE Total
BC
0
707
294
-523
67
-764
-486
-549
-276
-65
-1594
BS
1031
0
390
191
-53
185
-7
-192
-88
0
1458
BO
1137
715
0
650
64
146
79
-47
57
44
2844
BN
572
721
880
0
600
-1
6
-158
-58
133
2692
BE
1186
197
136
469
0
-515
-615
-462
-281
-121
-6
MS
313
669
262
53
-458
0
-607
-1772
-782
-273
-2596
MN
573
238
372
153
-379
-107
0
-1241
-827
-276
-1493
SO
-276
-168
-11
-153
-447
-1742
-1281
0
711
-46
-3413
SC
-36
-11
112
10
-234
-724
-649
1424
0
24
-85
SE
422
100
190
375
59
-68
43
789
282
0
2193
Total
4923
3169
2624
1222
-781
-3591
-3516
-2208
-1263
-579
0

Le candidat dispose de tous les résultats de la modélisation et il ne lui reste plus qu'à tenter d'interpréter les écarts entre les flux observés et les flux estimés. Ceci peut le conduire à trois types d'analyses :

C.1 Mobilité résiduelle et attractivité résiduelle

L'analyse des marges de la matrice des résidus permet de repérer les régions qui ont globalement reçu ou envoyés plus (ou moins) de migrants que ce que laissait prévoir le modèle. On peut en déduire des coefficients de mobilité résiduelle ou d'attractivité résiduelle.Une typologie des régions peut également être envisagée.

Tableau 5 : Analyse des marges de la matrice des résidus
i
Emissions
Reception
Mobilité
Attractivité
BC
-1594
4923
3328
6517
BS
1458
3169
4626
1711
BO
2844
2624
5468
-220
BN
2692
1222
3915
-1470
BE
-6
-781
-786
-775
MS
-2596
-3591
-6187
-995
MN
-1493
-3516
-5010
-2023
SO
-3413
-2208
-5620
1205
SC
-85
-1263
-1347
-1178
SE
2193
-579
1613
-2772

C.2 Flux résiduels
 

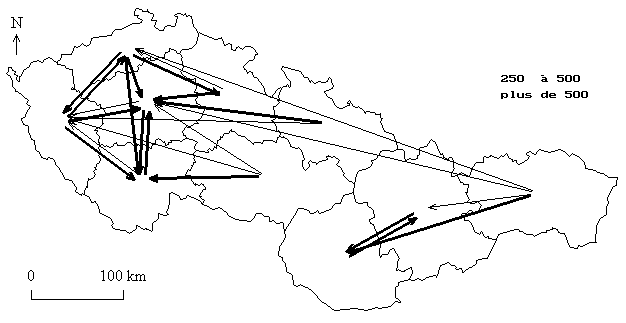
L'analyse des flux résiduels proprement dit permet de repérer les régions qui entretiennent des relations préférentielles (résidus positifs) et celles qui sont au contraire séparées par des effets de barrière (résidus négatifs). Une cartographie est indispensable pour bien reprérer les configurations spatiales des résidus et en déduire le rôle de nouveaux facteurs explicatifs à introduire dans le modèle.

Carte des plus forts résidus positifs


Carte des plus forts résidus négatifs

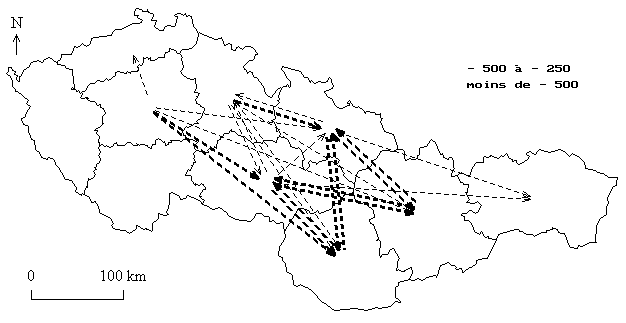
C.3 Evaluation d'un effet de barrière

Les cartes précédentes suggèrent l'existence d'une barrière migratoire entre les deux républiques, barrière dont on peut évaluer l'effet en procédant à la totalisation des flux observés et estimés dans le cadre des deux républiques :

Flux observés (Fij) et estimés (F*ij)  agrégés par républiques
Fij S T Total   Aij Fij
S
11980
8671
20651
  
1
68791
T
5926
56811
62737
  
0
14597
Total
17906
65482
83388
   Total
83388
             
F*ij S T Total   Aij F*ij
S
8794
13161
21955
  
1
57065
T
13161
48271
61433
  
0
26323
Total
21955
61433
83388
   Total
83388
             
Fij/F*ij S T Total   Aij Fij/F*ij
S
1.36
0.66
0.94
  
1
1.21
T
0.45
1.18
1.02
  
0
0.55
Total
0.82
1.07
1.00
   Total
1.00

On constate alors que les flux intra-républiques sont augmentés de 21% (coefficient multiplicateur 1.21) tandis que les flux inter-républiques sont réduits de 45% (coefficient multiplicateur 0.55). On en déduit la valeur de l'effet de barrière qui est la réduction des flux inter-républiques par rapport aux flux intra-république :

Effet de barrière = coeff intra/ coeff. inter = 1.21 / 0.55 = 2.2

Ceci permet de conclure que la limite des deux républiques correspond à une division par plus de deux des échanges, par rapport à la situation observée à l'intérieur de la république tchèque ou de la Slovaquie.

Pour plus de détails sur cet exemple, voir :

A RETENIR :
 
  • Une description complète d'une matrice de flux comporte plusieurs étapes (étude des marges, étude des couples origines-destinations, flux dominants)
  • Il faut bien distinguer la composante symétrique des flux (volume) et leur composante dissymétrique (solde). 
  • Les modèles d'interaction spatiale permettent de filtrer des effets banaux (capacité d'émission, capacité d'attraction, proximité spatiale) pour mettre à jour des effets spécifiques (préférences territoriales, barrières, …).
  • La cartographie des flux (observés ou résiduels) est difficile. Il faut être très sélectif.

Exercices

EXERCICE N°10
   Cartographie d'une matrice de flux
     sujet : Les migrations des étudiants dans la France de l'Ouest en 1993-1995

EXERCICE N°11
   Analyse des résidus d'un modèle d'interaction spatiale
     sujet : Les migrations entre les provinces de Belgique en 1989


 

Bibliographie