Tout le raisonnement développé dans la partie précédente pour mesurer les effets de barrière à l'aide des résidus d'un modèle d'interaction spatiale est fondé sur l’hypothèse que le principal déterminant géographique des échanges est la distance (interaction spatiale) et que les effets de barrière ou d’appartenance (interaction territoriale) ne sont qu’un déterminant secondaire, une composante résiduelle.
Or, cette hypothèse du primat de la distance sur l’appartenance
n’a rien d’évident sur le plan théorique et que, du coup,
l’évaluation des effets de barrière ou d’appartenance à
l’aide des résidus d’un modèle d’interaction spatiale peut
apparaître incorrecte sur le plan méthodologique. Un examen
rapide des principales théories permettant de rendre compte de la
décroissance des probabilités de relation avec la distance
(interaction spatiale) montre qu’elles pourraient s’appliquer tout aussi
bien à la décroissance des probabilités de relation
en fonction de l’appartenance (interaction territoriale).
Le paradigme économique : distance, coût, utilité.
L’explication économique de la mobilité, tout d’abord, se fonde sur l’hypothèse d’une relation entre la probabilité de relation et le coût de déplacement. Quelle que soit la mesure du coût de déplacement retenue (monétaire, psychologique, temporel), on suppose que le migrant est un être rationnel qui cherche à optimiser le rapport entre les avantages apportés par la mobilité et son coût. Si les opportunités de mobilité localisées en différents points de l’espace présentent les mêmes avantages pour le migrant, celui-ci cherchera uniquement à minimiser la fonction d’utilité constituée par le coût de déplacement. A priori, chaque migrant devrait donc choisir la destination qui correspond au coût de déplacement le plus faible, mais il se trouve en concurrence avec d’autres acteurs ce qui produit des effets de déséquilibre entre l’offre et la demande de mobilité pour certaines destinations. Il peut donc être amené, par le jeu de la concurrence à accepter une destination correspondant à un coût plus élevé ou à renoncer à son déplacement si le coût dépasse les avantages escomptés. Au total, la régulation opérée entre l’offre et la demande de mobilité doit conduire à un équilibre qui se traduit par une décroissance de la probabilité de relation en fonction du coût de déplacement. Ainsi formalisée, l’explication économique ne préjuge pas de la nature du coût de déplacement et de sa relation avec la localisation géographique des individus. Il faut donc introduire une hypothèse supplémentaire pour transformer le déterminant économique (coût de déplacement) en déterminant géographique.
Dans le cas des modèles d’interaction spatiale, on introduit l’hypothèse que les coûts de déplacement supportés par le migrants sont proportionnels à une certaine distance qui est supposé résumer un ensemble de contraintes pesant sur la décision de mobilité. Ainsi, dans le cas d’un changement de domicile, le choix d’une destination éloignée entraîne un coût monétaire (prix du déménagement), un coût psychologique (rupture des relations sociales avec les personnes du lieu d’origine), un coût relationnel (temps de déplacement entre le lieu d’origine et le lieu de destination, si le migrant décide d’y revenir périodiquement), etc. Dans le cas de transports de marchandises, le coût principal est l’énergie dépensée et le prix du transport en tonnes par kilomètres.
Or, ces différentes hypothèses peuvent tout aussi bien
s’appliquer à un modèle d’interaction territoriale où
le coût dépend non pas du nombre de kilomètres parcourus
mais du franchissement de limites de mailles territoriales. Ceci est particulièrement
évident pour les flux de marchandises ou le franchissement d’une
frontière politique entraîne le payement de taxes (coût
monétaire) et un délai d’attente plus ou moins long au poste
frontière (coût temporel). Mais on peut montrer qu’il en va
de même pour la mobilité des personnes. Une personne qui change
de régions ou de pays doit souvent s’acquitter d’un certain nombres
de formalités administratives qui impliquent des dépenses
de temps, d’énergie ou d’argent.. Enfin, si les limites de mailles
territoriales correspondent à des territoires auxquels les personnes
s’identifient, le fait de quitter son territoire d’appartenance implique
un coût psychologique non négligeable (attachement du migrant
à son lieu d’origine, hostilité éventuelle des habitants
du lieu de destination, etc.). On voit donc que les explications économique
de la mobilité par le coût de déplacement peuvent s’appliquer
indifféremment à des modèles d’interaction spatiale
ou à des modèles d’interaction territoriale.
Le paradigme de la circulation imparfaite de l’information
La théorie de la diffusion de l’information proposée par Hägerstrand permet de compléter l’explication économique en s’interrogeant sur l’information dont disposent les acteurs sur les différentes opportunités de destination. Le paradigme économique classique suppose en effet que chaque acteur est rationnel et pleinement informé, ce qui suppose qu’il connaît le coût et les avantages de chacune des relations qu’il peut éventuellement nouer. Or, dans les situations concrètes, ce paradigme n’est jamais vérifié. Tout flux matériel est en effet précédé par un contre-flux d’information qui permet à l’acteur d’opérer un choix rationnel entre plusieurs destinations mais dans un contexte d’information limitée. L’hypothèse centrale d’Hägerstrand est donc que la probabilité de relation matérielle entre deux personnes ou deux groupes dépend de la quantité d’information qui circule entre ces personnes ou ces groupes. Cette théorie permet par exemple de rendre compte du phénomène de l’auto-entretien des filières migratoires à longue distance. L’installation des premiers migrants génère un flux d’information entre le lieu d’origine et le lieu de destination, ce qui facilité l’arrivée de nouveaux migrants qui vont eux-mêmes générer à leur tour un flux d’information plus important, etc. Tout comme dans le cas du paradigme économique, l’existence d’une relation entre les flux de relation matérielles et les flux d’information ne préjuge pas du rôle des déterminants géographiques dans la circulation de l’information.
Dans le cas des modèles d’interaction spatiale, c’est
l’hypothèse d’une dégradation de l’information en fonction
de la distance qui permet de comprendre la décroissance des probabilités
de relation avec la distance. Ainsi, la personne qui souhaite changer de
domicile est beaucoup mieux informé des opportunités de migration
dans son environnement proche que dans son environnement éloigné.
A courte distance, elle peut disposer de relais locaux (parents, amis,
journaux, petites annonces, ...) qui facilitent son choix. A longue distance,
elle doit au contraire consentir une dépense plus ou moins importante
pour acquérir de l’information sur les opportunités de destination.
Confronté à deux opportunités équivalentes
de relation (e.g. deux opportunités d’emploi correspondant au même
salaire), l’acteur choisira souvent la plus proche car il dispose de plus
d’information à son sujet et pense ainsi pouvoir lever un certain
nombre d’incertitudes et agir " en connaissance de cause ".
La théorie de la circulation de l’information d’Hägerstrand
permet d’expliquer dans une certaine mesure la décroissance des
probabilités de relations avec la distance, mais elle s’applique
autant si ce n’est mieux aux modèles d’interaction territoriale.
C’est en effet Hägerstrand (1952, 1953) qui a formalisé le
premier la notion de barrière faisant obstacle à la diffusion
des innovations et à la circulation de l’information . Les obstacles
à la vie de relation, qu’ils soient physiques (chaîne de montagne,
lacs, fleuves), politiques (frontières, limites administratives)
ou sociaux (limite linguistique, discontinuité socio-culturelle)
se traduisent en effet souvent par une réduction des échanges
d’information entre les habitants situés de part et d’autre. Les
effets de ces barrières sur la circulation des informations peuvent
être multiples. Parmi les barrières qui empêchent totalement
la circulation des messages entre deux entités territoriales, on
peut distinguer des barrières super-absorbantes, qui détruisent
le message et l’émetteur, des barrières absorbantes,
qui détruisent simplement le message, et des barrières
réfléchissantes qui renvoient le message dans sa direction
d’origine mais sans le détruire. Mais ces situations de barrière
hermétique sont relativement rare. En général, on
a plutôt affaire à des barrières perméables
qui laissent passer une part plus ou moins importante des messages en fonction
de leur perméabilité . L’effet des barrières est donc
d’une part une concentration des messages et de l’information à
l’intérieur des mailles territoriales et d’autre part une faiblesse
relative des échanges d’information entre les mailles territoriales.
Concrètement, cela signifie qu’à distance égale, un
acteur dispose de plus d’information sur les opportunités de relation
avec les habitants de sa propre maille territoriale qu’avec ceux de mailles
territoriales différentes. Il aura donc tendance à privilégier
ces relations, même si elles se traduisent par un coût de relation
plus élevé. En outre, si la limite territoriale correspond
à un obstacle à l’acquisition de l’information (langues différentes),
le migrant doit dépenser une énergie plus importante pour
acquérir des renseignements sur les opportunités de mobilité
dans ce nouvel environnement. Le paradigme économique et le paradigme
de la circulation de l’information tendent donc à se renforcer et
à se compléter dans la justification des hypothèses
des modèles d’interaction territoriale.
Le paradigme sociologique des opportunités interposées
- Parmi les nombreuses critiques qu’a suscité l’application du
paradigme économique à l’étude des relations sociales,
l’une des plus importantes porte sur la nature de la distance utilisée
pour décrire les probabilités de relation. La plupart des
modèles d’interaction spatiale recourent à une mesure
continue de la distance, censée refléter l’influence
du coût de déplacement sur la décision d’établir
ou non une relation. L’utilisation d’une fonction de décroissance
de la probabilité de relation en fonction de la distance laisse
supposer que la perception du coût de la distance est la même
pour tous les habitants ou, à tout le moins, qu’il existe un comportement
moyen décrivant de façon continue la mobilité en fonction
de la distance. Or, cette hypothèse n’est valable que si les opportunités
de relation sont disposées de façon homogène dans
l’espace, c’est-à-dire si chaque acteur dispose d’autant d’opportunités
de relation à courte, moyenne ou longue distance. En général,
ce n’est pas le cas, ce qui signifie que les personnes situées dans
des zones à faible potentiel de relation doivent soit accepter un
coût de relation plus élevé, soit réduire leur
mobilité. Il est toutefois évident que lorsque la mobilité
répond à un besoin minimum de relations, c’est la
première solution qui sera adoptée et non pas la seconde.
La solution proposée par Stouffer pour lever cette difficulté consiste à modifier le rôle de la distance et à ne la faire intervenir que comme un critère ordinal permettant à l’acteur de classer les opportunités de relations. D’une manière générale, l’acteur procède donc à un classement des destinations possibles en fonction de leur rapport avantage/coût, puis il les examine de façon séquentielle. La probabilité de nouer une relation à longue distance ne dépend donc pas de la valeur absolue de cette distance mais du nombre d’opportunités situées à une distance inférieure. En effet, plus il y a d’opportunités interposées (situées à une distance plus courte), plus il est probable que le migrant aura déjà obtenu satisfaction et renoncé à examiner les opportunités éloignées.
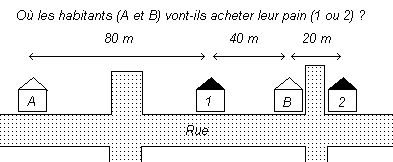
On peut illustrer la solution de Stouffer à l’aide de l’exemple présenté sur la Figure 1. Deux personnes localisées en des points A et B doivent aller acheter leur pain dans l’une des deux boulangeries localisées en 1 et en 2. Si l’on appliquait strictement la logique gravitaire, on serait amené à dire que la personne localisée en B a une plus forte probabilité de fréquenter la boulangerie 1 que la personne localisée en A, car elle est située à une distance deux fois plus faibles. Mais la personne localisée en B dispose d’une opportunité de relation plus proche et, si elle décide de minimiser son coût de déplacement, elle choisira de préférence la boulangerie n°2. Au contraire, la personne localisée en A ne dispose pas d’alternatives et la boulangerie n°1 est la plus proche de son domicile (pas d’opportunités interposées). Sauf à renoncer à manger du pain, elle acceptera donc un coût de déplacement plus élevé. Au total, contrairement à ce que laisserait présager le modèle gravitaire, la personne localisée en A a une plus forte probabilité de fréquenter la boulangerie n°1 que la personne localisée en B, si les deux acteurs adoptent une stratégie de minimisation de la distance. En fait, si l’on remplace la distance à vol d’oiseau par la distance ordinale (rang des opportunités) le comportement des acteurs apparaît bien conforme à la logique du modèle d’interaction spatiale.
Figure 1 : Un exemple d'application du problème de Stouffer
Le modèle de Stouffer permet donc non seulement d’améliorer les modèles d’interaction spatiale mais aussi de les rendre plus réalistes en démystifiant le rôle de la distance. La décroissance des probabilités de relation avec la distance ne correspond en effet pas nécessairement à un effet mécanique mais peut-être interprétée à l’aide d’une hypothèse psychologique de comportement. La critique de Stouffer porte d’ailleurs essentiellement sur les modèles de type gravitaire mais elle ne remet pas véritablement en cause les modèles à double contrainte. Ceux-ci incorporent en effet une situation de concurrence pour les destinations qui permet de prévoir des situations du type de celle qui est présentée sur la Figure 1. En effet, si l’on suppose que chaque habitant fréquente une seule boulangerie et que chaque boulangerie a un seul client (double contrainte), la situation la plus probable dans une perspective de minimisation du coût de déplacement est bien que l’habitant A fréquente la boulangerie n°1 et que l’habitant B fréquente la boulangerie n°2.
Le modèle de Stouffer permet donc de valider les hypothèses des modèles d’interaction spatiale et de les dédouaner de l’accusation de projeter des hypothèses mécanistes sur le comportement spatial des individus. Toutefois, il reste à démontrer la validité de l’hypothèse de comportement des acteurs qui est sous-jacente à la théorie de Stouffer. Les modèles d’interaction spatiale postulent en effet que les acteurs ordonnent les opportunités de relation en fonction de la distance, supposée refléter le coût de réalisation des relations. Ceci revient donc à reprendre le paradigme économique dont nous avons vu précédemment qu’il s’appliquait tout aussi bien aux modèles d’interaction territoriale. Ceci suppose également que l’acteur est pleinement informé de l’ensemble des opportunités de relation et que le classement qu’il opère tient compte de l’ensemble de l’information. Or, comme nous l’avons montré à propos du modèle d’Hägerstrand, il n’est pas obligatoire que l’acteur dispose d’une information exhaustive et le classement des opportunités qui sert de base à son choix peut être le résultat d’une information incomplète. Toutes choses égales quant à la distance, l’acteur peut disposer sur une information plus complète concernant les opportunités de relation situées à l’intérieur de sa propre maille territoriale que sur les opportunités de relation situées dans des mailles territoriales différentes. Il peut donc effectuer un classement qui dépende non seulement de la distance mais aussi de l’appartenance, ce qui le conduira à adopter un comportement à la fois spatial et territorial. Il peut aussi arriver que le migrant choisisse délibérément de privilégier l’appartenance territoriale comme critère de choix dans ses destinations. Ainsi, on peut imaginer des formes de classement emboîtés ou un migrant décide (1) de migrer si possible à l’intérieur de sa maille d’appartenance et (2) de prendre la destination la plus proche, toutes choses égales quant à l’appartenance.
Dans l’exemple de la Figure 1 on peut imaginer que ce sont les
enfants qui vont chercher le pain et que les parents souhaitent éviter
qu’ils traversent des rues. La règle de décision fixée
par les parents est donc bien un choix emboîté qui consiste
(1) à traverser le moins de rues possibles (effet territorial) et
(2) à choisir la boulangerie la plus proche, toutes choses égales
quant au nombre de rues traversées. Dans ce cas, les habitants de
la maison B se rendront de préférence à la boulangerie
n°1 qui, bien que plus éloigné, à l’avantage de
se trouver dans le même pâté de maison (appartenance)
et d’éviter d’avoir à traverser une rue (limite territoriale).
Pour les habitants de la maison A, il faudra de toute manière franchir
au moins une rue pour aller chercher le pain, et il sera peut-être
même nécessaire de se rendre à la boulangerie n°2
car les habitants de A, qui sont plus proche, auront pu plus facilement
saisir les opportunités situés dans la boulangerie n°1
(baguette).
Les modèles d’interaction géographique.
- L’examen des fondements théoriques des modèles d’interaction
spatiale montre donc que les hypothèses théoriques qui justifient
leur emploi en sciences sociales s’appliquent tout aussi bien au modèle
d’interaction territoriale. Il n’y a donc pas de raison théorique
valable de privilégier la distance par rapport à l’appartenance
dans la recherche des déterminants géographiques des relations
sociales. Bien au contraire, il apparaît que dans chacune des théories
proposées, les deux facteurs sont complémentaires et étroitement
imbriqués sur le plan conceptuel. Analyser séparément
les deux effets de distance et d’appartenance, comme nous l’avons fait
dans la partie précédente, risque donc de faire manquer une
dimension fondamentale du phénomène et de conduire à
des conclusions incorrectes sur les rôles respectifs de la proximité
spatiale et de l’appartenance territoriale dans le comportement des acteurs.
Aussi, nous proposons de rassembler sous le terme général de modèles d’interaction géographique l’ensemble des modèles qui proposent de décrire l’intensité des relations sociales en fonction de la proximité spatiale ou de l’appartenance territoriale. Les modèles d’interaction géographique regroupent donc les modèles d’interaction spatiale (probabilité de relation en fonction de la distance), les modèles d’interaction territoriale (probabilité de relation en fonction de l’appartenance) et les modèles d’interaction spatiale et territoriale qui prennent simultanément en compte les deux effets de distance et d’appartenance.
4.3.2 Estimation déductive des effets de barrière (test d'une partition connue)
En nous limitant au cas des modèles multiplicatifs d’interaction
migratoire à double contrainte et à diagonale vide, nous
allons essayer de définir une famille de modèle d’interaction
géographique comprenant des modèles d’interaction spatiale
(vus au chapitre précédent), des modèles d’interaction
territoriale et des modèles d’interaction spatiale et territoriale.
Nous nous limiterons dans un premier temps au cas des modèles d’interaction
territoriale les plus simples, c’est-à-dire ceux qui étudient
l’effet de l’appartenance commune et ne dépendent que d’un seul
paramètre (le coefficient de perméabilité des limites
territoriales). Les autres formes de modèles d’interaction territoriale
seront brièvement évoquées mais ne seront pas développées.
Les modèles d’interaction territoriale
Si l’on repart du modèle d’interaction à double contrainte défini au chapitre précédent, on voit que le passage d’un modèle d’interaction spatiale à un modèle d’interaction territoriale consiste simplement à modifier l’hypothèse faite sur le facteur d’éloignement (matrices I) et sur la fonction d’interaction f(Iij) s’appliquant à ce facteur d’éloignement.
Si l’on suppose connue l’appartenance des unités territoriales
à différentes mailles territoriales, la manière la
plus simple de définir un modèle d’interaction territoriale
est de supposer que l’intensité des relations dépend de la
distance d’appartenance commune, c’est-à-dire de l’appartenance
des unités territoriales à une même maille territoriale
(Aij=0)
ou à deux mailles territoriales différentes
(Aij=1).
Le facteur d’éloignement comportant deux modalités, on peut
donc définit un modèle à deux paramètres indiquant
l’accroissement relatif des flux intra-maille (b
0)
et la réduction relative des flux inter-mailles (b
1)
:
(1) Fij = ai.Oi.bj.Dj.
b
0(1-Aij)
. b
1Aij
Toutefois, dans la mesure où le modèle est à double contrainte, l’un des deux paramètres va être absorbé par les contraintes de conservation des lignes et des colonnes et il est plus simple d’introduire un seul paramètre correspondant à la valeur de l’effet de barrière (g ) ou du coefficient de perméabilité (1/g ):
(2) Fij = ai.Oi.bj.Dj. (1/g )Aij
Le modèle postule donc simplement que les flux dépendent des capacités d’émission et de réception des lieux d’origine et de destination et que les flux franchissant une limite de maille territoriale subissent une réduction moyenne correspondant à une division par g . L’hypothèse sous-jacente à ce modèle est l’existence d’un effet de barrière complet et homogène, c’est-à-dire d’une réduction de tous les flux qui franchissent une limite territoriale par un même facteur.
On peut naturellement construire des modèles d’interaction territoriale
plus complexe. Ainsi, si l’on suppose que l’effet d’appartenance ne correspond
pas nécessairement à un effet de barrière complet,
il faudra définir autant de paramètres qu’il y a de couples
d’appartenances possibles. Par exemple, si l’on a défini une partition
en 3 classes d’appartenance X, Y et Z, on doit théoriquement estimer
neuf coefficients d’interaction b
XX,
b
XY,
b
XZ,
b
YX,
b
YY,
b
YZ,
b
ZX,
b
ZY,
b
ZZ.
En réalité, certains de ces paramètres seront absorbés
par les contraintes de conservation des flux imposées aux modèles
et, dans le cas d’une partition en k mailles territoriales, il n’y aura
que (k-1)2 paramètres à estimer.
Ainsi, dans le cas d’une partition en trois classes, il suffit d’ajuster
les quatre paramètres b
XX,
b
XY,
b
YX
et b
YY
pour
obtenir un ajustement optimal du modèle. On définira donc
quatre matrices XX, YY, XY et XY composées de 0 et de 1 et telles
que (par exemple) XX(i,j) =1 si i appartient à X et j appartient
à X. Le modèle d’interaction territoriale sera alors de la
forme :
(3) Fij = ai.Oi.bj.Dj.
b
XXXXijj.
b
XYXYijj.
b
YXYXijj.
b
YYYYij
On peut remarquer que, dans le cas d’un modèle à double contrainte et d’une partition en deux classes, le calcul des coefficients d’appartenance est inutile puisqu’il suffit de calculer un seul paramètre pour que tous les autres soient absorbés par les contraintes du modèle. Il est donc plus intéressant de calculer la valeur de l’effet de barrière plutôt que celle d’un des quatre coefficients d’appartenance.
Une troisième possibilité d’enrichissement des modèles d’interaction territoriale consiste à prendre en compte l’effet simultané de plusieurs partitions. Ces partitions peuvent être indépendantes (par exemple une division nord-sud et une division est-ouest) ou bien correspondre à un emboîtement de maillages hiérarchisés (par exemple l’appartenance au républiques et aux régions). Dans ce dernier cas, les effets de barrière sont cumulatifs puisque tout effet de barrière concernant un niveau territorial supérieur (les républiques) implique nécessairement une valeur supérieur ou égale à l’effet de barrière subit au niveau territorial inférieur. Ainsi, si l’on définit par REPij l’appartenance de deux districts à une même république et par REGij l’appartenance de deux districts à une même région (les républiques étant composées de régions), le modèle d’interaction territoriale permettra d’estimer deux paramètres d’effet de barrière :
(4) Fij = ai.Oi.bj.Dj.
(1/g
REP)REPij.(1/g
REG)REGij
Le paramètre g
REG
correspondra à l’effet de barrière lié au franchissement
des limites régionales tandis que le paramètre g
REP
définira l’effet de barrière spécifique lié
au franchissement des limites de républiques. L’effet de barrière
global lié au franchissement des limites de républiques sera
égale au produit des deux effets (g
REG
. g REP) puisque
toute limite de république est aussi une limite de région
dans le cas d’un maillage strictement emboîté. On peut également
calculer un effet de barrière régional spécifique
en ne retenant dans le calcul de que les limites de régions situées
à l’intérieur de la même république. Il est
ainsi possible de décomposer les effets de barrière induits
par une hiérarchie de maillages emboîtés et de déterminer
à quel niveau d’organisation territoriale s’observent les plus forts
effets d’appartenance.
A titre d’exemple, nous avons pu montrer à travers l’étude
des migrations entre les 109 districts de Tchécoslovaquie en 1989
(Grasland C., 1994) que l’effet de barrière inter-république
était de 2.7 et l’effet de barrière inter-régional
était de 1.6. L’influence spécifique du franchissement de
la limite des deux républiques correspond donc à un effet
de barrière de 2.7/1.6 = 1.7. Par la suite, si on calcule l’effet
de barrière inter-régional à l’intérieur de
chacune des deux républiques, on voit qu’il est de 1.3 en république
tchèque et de 1.1 en Slovaquie .
Même dans leur formulation la plus simple (calcule d’un seul paramètre
mesurant l’effet de barrière associé à une partition),
les modèles d’interaction territoriale fournissent souvent des descriptions
des relations sociales dont la qualité est voisine de celle des
modèles d’interaction spatiale. Ainsi, dans le cas des migrations
entre les 10 régions de Tchécoslovaquie en 1985-90, le pouvoir
explicatif d’un modèle d’interaction territoriale fondé sur
l’appartenance aux deux républiques est de 71.6% (critère
r*2 mesurant le pouvoir explicatif du modèle
une fois pris en compte l'effet des marges) alors que les modèles
d’interaction spatiale sur la distance ont un pouvoir explicatif de 67.8%
(modèle exponentiel) ou 71.6% (modèle Paréto). Naturellement
cette équivalence des modèles d’interaction spatiale et des
modèles d’interaction territoriale n’est pas une règle absolue.
Le pouvoir explicatif de l’appartenance dépend de l’importance de
l’effet de barrière et peut donc varier au cours du temps. Ainsi,
si l’on considère les migrations entre les 10 régions de
Tchécoslovaquie en 1961-65, le pouvoir explicatif du modèle
d’interaction territoriale n’est que de 55 .7% alors que celui des modèles
d’interaction spatiale est nettement supérieur (64.4 % pour le modèle
exponentiel et 72.5 % pour le modèle Paréto). Ceci semble
indiquer que le pouvoir explicatif de la distance est demeuré relativement
stable au cours du temps, alors que l’influence de l’appartenance sur le
comportement des migrants s’est renforcée.
L’examen des coefficients de barrière calculés directement
à l’aide du modèle d’interaction territoriale ou indirectement
à l’aide des résidus des modèles d’interaction spatiale
confirme ce renforcement de l’effet de barrière en Tchécoslovaquie
entre 1961 et 1990, mais elle met en évidence un problème
particulièrement gênant : les coefficients de barrière
calculés directement à l’aide du modèle d’interaction
territoriale sont considérablement plus élevés que
ceux obtenus à l’aide des résidus des modèles d’interaction
spatiale. Ainsi, en 1961-65, l’effet de barrière estimé
par le modèle d’interaction territoriale est de 3.27 alors que celui
que nous avions estimé dans le chapitre précédent
à l’aide des résidus d’un modèle d’interaction spatiale
était deux fois plus faible (1.58). De même, en 1986-1990
l’effet de barrière estimé par le modèle d’interaction
territoriale est de 4.55 alors que celui estimé à l’aide
des résidus d’un modèle d’interaction spatiale n’est que
de 1.96.
Le fait que les effets de barrière calculés à l’aide des résidus d’un modèle d’interaction spatiale soient plus faible que les effets de barrière calculés directement à l’aide d’un modèle d’interaction spatiale s’explique par l’existence d’une forte corrélation entre la proximité et l’appartenance. Dans le cas de la Tchécoslovaquie, la disposition des deux républiques et l’allongement du territoire génèrent une forte dépendance entre la proximité de deux régions et leur appartenance à la même république ou, symétriquement, entre l’éloignement de deux régions et la probabilité qu’elles ont d’appartenir à deux républiques différentes. La faiblesse des flux à longue distance peut donc s’expliquer aussi bien par l’effet de la distance (interaction spatiale) que par l’effet de l’appartenance (interaction territoriale). Du coup, un modèle qui ne prend en compte qu’un seul des deux effets (la distance ou l’appartenance) risque de prendre en compte tout ou partie de ce qui est imputable à l’autre facteur. Le modèle d’interaction territorial génère des coefficients de barrière très élevés car il impute à l’appartenance territoriale (républiques différentes) des effets qui sont peut être simplement liés à l’éloignement. Quant au modèle d’interaction spatiale, il risque de surestimer l’effet de la distance en lui attribuant une partie des effets de l’appartenance. Les effets d’appartenance étant partiellement pris en compte par la distance, les résidus du modèle d’interaction spatiale auront donc tendance à sous-estimer l’effet de barrière.
On peut donc conclure que, lorsqu’il existe une corrélation entre la distance et l’appartenance, les deux effets d’interaction spatiale et d’interaction territoriale doivent être estimés simultanément et non pas séparément. Plus la corrélation entre les deux facteurs est importante, plus l’estimation séparée des paramètres de distance et d’appartenance risque de faire apparaître des biais et de conduire à des erreurs d’interprétation. Le cas des migrations entre les 11 provinces de Belgique en fournit d’ailleurs une preuve a contrario. Si l’on examine l’effet de barrière correspondant à une division entre les provinces néerlandophones et les provinces francophones de 1964 à 1989, on observe assez peu de différences entre les coefficients de barrière estimés à l’aide du modèle d’interaction territoriale et ceux déduits de l’analyse des résidus d’un modèle d’interaction spatiale. Cette stabilité s’explique par la configuration particulière du pays (allongement dans le sens des unités linguistiques) et par la très faible dépendance entre la proximité spatiale et l’appartenance territoriale.
Le cas de la Belgique est cependant très particulier et, dans
l’immense majorité des cas, il existe une forte corrélation
entre la distance séparant deux unités spatiales et le fait
qu’elles appartiennent à une même maille territoriale ou à
deux mailles territoriales différentes. Cette corrélation
s’explique très simplement par la contrainte de contiguïté
politico-administrative, c’est-à-dire par le fait que les unités
composant une maille territoriale forment en général un ensemble
connexe et sont donc en moyenne plus proches les unes des autres que deux
unités spatiales prises au hasard.
Les modèles d’interaction spatiale et territoriale
Les modèles d’interaction spatiale et territoriale partent de l’hypothèse que les relations qui se nouent entre les habitants dépendent simultanément de la distance et de l’appartenance. L’hypothèse la plus simple que l’on puisse formuler est que les deux effets se combinent de façon multiplicative, c’est-à-dire que l’effet de barrière lié au franchissement d’une limite territoriale est le même, quelle que soit la distance de relation. Si l’on admet cette hypothèse de proportionnalité, on peut définir comme suit un modèle d’interaction spatiale et territoriale à double contrainte :
(5) Fij = ai.Oi.bj.Dj.
f(dij) .(1/g
)Aij
avec f(dij) = dij-a
: modèle Paréto
ou f(dij) = exp-a
dij : modèle exponentiel
L’ajustement de ces modèles est relativement complexe car il suppose le recours à deux procédures itératives emboîtées, l’une pour l’estimation des paramètres de double contrainte (ai et bj) et l’autre pour la détermination du couple de paramètre (a ,g ) assurant la meilleure qualité d’ajustement (critère de minimisation du chi-2). En effet, l’ajustement des paramètres de freinage de la distance (a ) et d’effet de barrière (g ) étant effectué de façon simultanée, il faut examiner l’ensemble de la surface d’ajustement (r2) correspondant à ces deux paramètres pour déterminer la valeur de l’optimum global. Des méthodes d’ajustement non-linéaire permettent de faciliter la recherche de cet optimum global mais il faut vérifier que la solution obtenue corresponde bien à un optimum global et non pas à un optimum local . Les programmes informatiques que nous avons mis au point pour ajuster de tels modèles sont encore des prototypes qui ne peuvent traiter qu’un nombre limité d’unités territoriales et nécessitent un temps de calcul assez long. Des solutions informatiques et statistiques plus rapides et plus performantes seront prochainement disponibles grâce à une coopération entre le M.E.T.L., l'IMAG (Grenoble), le LABSAD (Grenoble) et l'équipe P.A.R.I.S. (CNRS-Paris)
Les résultats sont toutefois à la hauteur de l’effort consenti car les modèles d’interaction spatiale et territoriale se révèlent nettement plus performants que les simples modèles d’interaction spatiale ou d’interaction territoriale. Dans le cas des migrations en Tchécoslovaquie (Tableau 1) , l’estimation simultanée des effets de proximité et d’appartenance conduit à des qualités d’ajustement r*2 de l’ordre de 90 %, alors que les modèles qui séparent les deux effets ont des qualités d’ajustement qui ne dépassent guère les 70 %. Ce gain explicatif considérable montre que les effets d’appartenance et de proximité ne sont pas redondants mais complémentaires. Les modèles d’interaction spatiale et territoriale semblent donc très utile pour décrire et prévoir le comportement des populations et ils semblent particulièrement adapté à la situation des échanges à l’intérieur de territoires présentant de forts clivages historiques, politiques, sociaux ou culturels .
Toutefois, plus que leur intérêt opérationnel, c’est
l’intérêt théorique des modèles d’interaction
spatiale et territoriale pour la connaissance des phénomènes
d’intégration sociale que nous voudrions souligner. Les paramètres
de réduction des interactions en fonction de la distance (a
) et de l’appartenance (g ) sont en effet estimés
simultanément, de sorte que leur dépendance réciproque
est contrôlée. Leur valeur est donc beaucoup plus fiable que
précédemment et l’interprétation que l’on peut en
faire sera beaucoup plus précise. En effet, dans un modèle
d’interaction spatiale et territoriale le paramètre (a
) mesure la décroissance des relations avec la distance toutes
choses égales quant à l’appartenance tandis que le paramètre
(g ) mesure l’importance de l’effet de barrière
toutes choses égales quant à la distance. L’exemple des
migrations entre les 11 régions de Tchécoslovaquie montre
que les valeurs correctes de ces paramètres sont parfois très
éloignées de celles qui avaient été obtenues
à l’aide d’une estimation séparée. Ainsi, pour les
migrations en Tchécoslovaquie de 1961 à 1965, le frein de
la distance toutes choses égales quant à l’appartenance est
de -1.02 pour le modèle Paréto et de -0.0036 pour le modèle
exponentiel. La même estimation faite à l’aide d’un simple
modèle d’interaction spatiale (donc, ne tenant pas compte de l’appartenance)
conduisait à une nette surestimation de cet effet de la distance
(respectivement -1.34 et -0.0064). Quant à l’effet de barrière
sa valeur correcte (toutes choses égales quant à la distance)
est environ de 2.1, alors que les estimations obtenues précédemment
étaient soit trop élevés (modèle d’interaction
territoriale), soit trop faible (résidus d’un modèle d’interaction
spatiale).
L’estimation simultanées des paramètres de distance et
d’appartenance par un modèle d’interaction spatiale et territoriale
apparaît d’autant plus nécessaire que les biais introduit
par les autres méthodes ne sont pas systématiques. Ainsi,
dans le cas de la Belgique, les paramètres de barrière estimés
par le modèle d’interaction territoriale sont plus faibles que ceux
estimés par le modèle complet alors que, dans le cas de la
Tchécoslovaquie c’est l’inverse qui se produit. Une comparaison
valable de l’effet de barrière dans les deux pays suppose donc que
l’on recoure dans chacun des cas à un même modèle prenant
simultanément en compte les effets d’appartenance et de proximité.
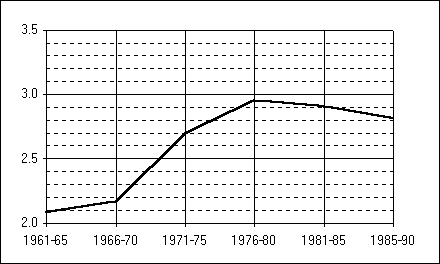
Exemple d’application : l’évolution de l’effet de barrière en Tchécoslovaquie et en Belgique (1961-1990)
Si l’on prend comme référence le modèle qui fournit le meilleur ajustement (Paréto), on peut montrer que l’effet de barrière était sensiblement du même ordre de grandeur dans les deux pays au début des années 1960 et correspondait à une division par deux des flux entre les deux républiques de Tchécoslovaquie ou entre les deux régions linguistiques de Belgique. La comparaison des situations à la fin des années 1980 montre que l’accroissement de l’effet de barrière a été plus marqué en Belgique (+ 55 %) qu’en Tchécoslovaquie (+35 %). Le rythme temporel de cet accroissement de l’effet de barrière apparaît également différent. En Belgique, on observe deux phases d’accroissement rapide de l’effet de barrière (1964-1974 et 1979-1984) séparées par un palier. Entre 1984 et 1989, l’effet de barrière migratoire entre les deux régions linguistiques de Belgique semble s’être stabilisé. En Tchécoslovaquie on observe une seule phase d’accroissement rapide de l’effet de barrière entre 1970 et 1980. Au cours des années 1980, l’effet de barrière entre les deux républiques de Tchécoslovaquie tend à se stabiliser voire à diminuer légèrement. Les deux pays montrent donc un renforcement similaire de l’opposition entre deux composantes territoriales ayant des comportement migratoires de plus en plus autonomes. Cette accroissement de la division du champ migratoire national s’est opéré dans les deux pays de façon précoce et a peut être été influencé par la mise en place d’une reconnaissance administrative des entités territoriales : réforme linguistiques en Belgique (1963) ; mise en place du système fédéral en Tchécoslovaquie (1969). Il est toutefois difficile de tirer des conclusions trop radicale d’une simple analyse de la mobilité des populations. La fragmentation du champ migratoire n’est qu’une composante, un marqueur, des divisions croissantes du corps social qui se sont opérées dans les deux pays et qui trouvent leur racine dans la résurgence de divisions historiques et culturelles plus profondes. Il semble d’ailleurs exister un décalage entre la modification du comportement des habitants (accroissement de l’effet de barrière) et la sanction politique de ces divisions sociales par un changement de maillage : mise en place du système fédéral en Belgique (1993) ; séparation de la Tchécoslovaquie en deux Etats (1993). Dans les deux cas, la réforme politique ou administrative s’est opérée dans un contexte de stabilité (Belgique) voire de réduction (Tchécoslovaquie) des divisions sociales, telles que l’on peut les mesurer à l’aide des données migratoires.
Figure 2 : Evolution de l'effet de barrière migratoire entre la république tchèque et la Slovaquie (1961-1990)
Figure 3 : Evolution de l'effet de barrière migratoire entre les provinces francophones et néerlandophones de Belgique (1964-1989)
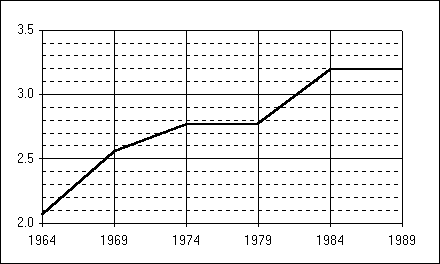
Tableau 1 : Modélisation des échanges migratoires entre les 10 régions de Tchécoslovaquie de 1961 à 1990
| MODELE A | Qualité de | Paramètres | Paramètres déduits de | Effet de barrière | ||||||
| DOUBLE | l'ajustement | estimés | l'analyse des résidus | |||||||
| CONTRAINTE |
|
|
|
|
|
|
|
|
|
|
| Absence d'interaction | ||||||||||
| 1961-65 |
|
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
| 1961-65 |
|
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
| Interaction spatiale | ||||||||||
| (Paréto) | 1961-65 |
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
| Interaction spatiale | ||||||||||
| (expon.) | 1961-65 |
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
| & interaction spatiale | ||||||||||
| (Paréto) | 1961-65 |
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
| & interaction spatiale | ||||||||||
| (expon.) | 1961-65 |
|
|
|
|
|
|
|
|
|
| 1966-70 |
|
|
|
|
|
|
|
|
|
|
| 1971-75 |
|
|
|
|
|
|
|
|
|
|
| 1976-80 |
|
|
|
|
|
|
|
|
|
|
| 1981-85 |
|
|
|
|
|
|
|
|
|
|
| 1985-90 |
|
|
|
|
|
|
|
|
|
|
Tableau 2 : Modélisation des échanges migratoires entre les 11 provinces de Belgique (1964-1989)
| MODELE A | Qualité de | Paramètres | Paramètres déduits de | Effet de barrière | ||||||
| DOUBLE | l'ajustement | estimés | l'analyse des résidus | |||||||
| CONTRAINTE |
|
|
|
|
|
|
|
|
|
|
| Absence d'interaction | ||||||||||
|
1964
|
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
|
1964
|
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
| Interaction spatiale | ||||||||||
| (Paréto) |
1964
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
| Interaction spatiale | ||||||||||
| (expon.) |
1964
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
| & interaction spatiale | ||||||||||
| (Paréto) |
1964
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
| Interaction territoriale* | ||||||||||
| & interaction spatiale | ||||||||||
| (expon.) |
1964
|
|
|
|
|
|
|
|
|
|
|
1969
|
|
|
|
|
|
|
|
|
|
|
|
1974
|
|
|
|
|
|
|
|
|
|
|
|
1979
|
|
|
|
|
|
|
|
|
|
|
|
1984
|
|
|
|
|
|
|
|
|
|
|
|
1989
|
|
|
|
|
|
|
|
|
|
|
4.3.3 Estimation inductive des effets de barrière (recherche d'une partition inconnue)
La mise en évidence d’une dépendance entre les phénomènes
d’interaction spatiale et d’interaction territoriale nous a conduit à
proposer un modèle général d’analyse de l’interaction
spatiale et de l’interaction territoriale qui est plus satisfaisant que
les modèles fondés sur l’analyse des résidus d’un
modèle d’interaction spatiale. Mais du coup, nous nous trouvons
confronté à une difficulté majeure car les méthodes
développées dans le chapitre précédent pour
mettre en évidence des structures territoriales à partir
de l’analyse des résidus apparaissent incorrectes. En effet,
comme les modèles d’interaction spatiale sont biaisés (surestimation
de l’effet de la distance), les résidus qu’ils produisent le sont
également. Du coup, les structures territoriales que l’on peut mettre
en évidence à partir de ces résidus (effets de barrière
complets ou incomplets, effets d’appartenance) ne sont pas nécessairement
celles qui traduisent le mieux le comportement territorial des migrants.
Définition du problème de la partition inconnue
Le problème de la partition inconnue est à la fois
d’une grande simplicité conceptuelle et d’une grande complexité
mathématique. Un territoire composé de n unités
territoriales peut en effet être subdivisé en un nombre fini
de partition territoriales. En l’absence de contraintes particulières
(nombre de classes, contrainte de contiguïté, etc.) le nombre
maximum de partitions différentes est égal à nn
.
Chacune de ces partitions peut servir de base au calcul d’un modèle
d’interaction spatiale et territoriale et, après ajustement des
paramètres de distance et de barrière, on peut lui attribuer
un pouvoir explicatif qui correspond à la qualité de l’ajustement
réalisé à l’aide de ce modèle. Les partitions
étant en nombre fini, il existe donc nécessairement une partition
optimale, c’est-à-dire un découpage du territoire en classes
qui permet d’obtenir une description optimale de l’influence de la distance
et de l’appartenance sur le comportement des migrants. C.Q.F.D.
Il faut toutefois faire d’emblée deux réserves sur le
caractère optimal de la partition obtenue.
- La partition optimale ne l’est qu’au sens d’un certain modèle
et d’un certain critère d’ajustement. Si l’on change la forme du
modèle (e.g. utilisation de plusieurs coefficients d’appartenance
à la place d’un seul coefficient de barrière) ou si l’on
change le critère de mesure de la qualité d’ajustement (e.g.
utilisation du maximum de vraisemblance ou des moindres carrés à
la place du critère du chi-deux), le classement des partitions risque
d’être modifié et la partition "optimale " ne sera plus nécessairement
la même.
Même si l’on fixe la forme du modèle comme nous l’avons fait précédemment (recherche de deux paramètres a et g à l’aide d’un modèle à double contrainte visant à minimiser le chi-2 de l’erreur), il n’est pas obligatoire que la partition optimale corresponde à une division de l’espace en unités territoriales fortement intégrées et séparées par des effets de barrière. Il est en effet possible que la partition optimale corresponde à un effet d’anti-barrière, c’est-à-dire à une division de l’espace en entités territoriales ou la probabilité de relation intra-maille est plus forte que la probabilité de relation inter-maille, toutes choses égales quant à la distance. Ce résultat n’est paradoxal qu’en apparence. En effet, une partition conduisant à une valeur de g supérieure à 1 (anti-barrière) correspond bien à une forme d’intégration sociale puisqu’elle définit des entités territoriales qui maximisent les relations entre les personnes ayant des appartenances différents. Un Etat qui souhaite développer des relations entre des groupes qui s’ignorent pourrait très bien choisir de fragmenter ces groupes et de les regrouper dans des mailles administratives différentes afin de créer de nouvelles opportunités de brassage social. Les partitions débouchant sur des anti-barrières correspondent donc à une stratégie d’intégration territoriale globale (renforcement des échanges entre toutes les composantes du système) tandis que les partitions fondées sur des barrières correspondent à une stratégie de renforcement de l’intégration territoriale locale (renforcement des échanges entre des sous-systèmes déjà constitués). En tout état de cause, il existe un lien entre les deux formes de partition puisque toute partition correspondant à des barrières territoriales implique l’existence de partition perpendiculaires générant des anti-barrières. Ce n’est que si un système est faiblement structuré que l’on ne peut pas mettre en évidence de partition territoriales de type barrière ou anti-barrière se détachant nettement des autres.
Un exemple d’application du problème de la partition inconnue
Supposons que nous voulions vérifier si la division en deux
républiques correspond à la partition qui donne le meilleur
ajustement des flux entre les 10 régions tchécoslovaques
en 1961-65 à l’aide d’un modèle d’interaction spatiale et
territoriale. La seule façon de s’en assurer est de tester l’ensemble
des partitions et de mesurer leur qualité d’ajustement. Toutefois,
même avec 10 régions, le nombre de partition possible est
très élevé. On peut donc poser un certain nombre de
conditions restrictives afin de n’examiner que les partitions qui sont
comparables à la division en deux républiques. On limitera
donc la recherche aux partitions qui vérifient les conditions suivantes
:
- partition en deux entités spatiales (fixation du nombre de classes)
- entités spatiales composées de régions connexes (contrainte de continuité territoriale)
Seules 48 partitions vérifient ces deux conditions et l’on
peut alors procéder à un examen exhaustif de leurs paramètres
(a ,g ) et de leur
qualité d’ajustement (r2). L’examen
du paramètre de barrière montre que 25 partitions correspondent
à des effets de barrière (g <
1) et 23 à des effets d’anti-barrière (g
>1). Le classement des partitions en fonction de la qualité d’ajustement
des modèles d’interaction spatiale et territoriale (Figure 4)
montre que la division en deux républiques (partition B1) n’arrive
qu’en deuxième position avec une qualité d’ajustement de
93.1% . La partition optimale (A1) a une qualité d’ajustement légèrement
supérieure (93 .2%) et correspond à un modèle d’anti-barrière
dont les paramètres sont a = -1.82 et
g
=0.57. Elle oppose quatre régions de Bohême (nord, centre,
ouest et sud) au reste du pays. Comme il s’agit d’un effet d’anti-barrière,
les flux intra-maille sont proportionnellement plus faibles que les flux
inter-mailles, toutes choses égales quant à la distance.
En effet, cette partition regroupe des régions qui échangent
moins de migrant que ce que laisserait présager leur proximité
(e.g. Bohême-nord et Bohême-centre ou Moravie-sud et Slovaquie-ouest)
tandis qu’elle sépare des régions qui échangent plus
que ce que laisserait prévoir leur proximité (e.g. Slovaquie-ouest
et Bohême-nord ou Bohême-centre et Bohême-sud). Il n’y
a donc rien de paradoxal au fait que le meilleur modèle descriptif
soit un modèle d’anti-barrière regroupant les régions
qui sont les moins intégrées.
L’examen de l’histogramme des qualités d’ajustement montre d’ailleurs que 6 des 7 meilleures partitions correspondent à des modèles de type anti-barrière (Figure 5) et se détachent nettement des partitions suivantes dont les qualités d’ajustement sont équivalentes et beaucoup plus faibles. Les meilleures partitions avec effet d’anti-barrière présentent d’ailleurs de fortes ressemblances entre elles (e.g. A1 et A2 ou A3 et A5) puisqu’elles visent toutes à regrouper les régions proches qui échangent moins de migrant que ce que laisserait prévoir leur proximité. Ceci explique sans doute pourquoi les meilleures partitions avec effet d’anti-barrière ont des qualités d’ajustement assez voisine, aucune ne se détachant nettement des autres.
Il n’en va pas de même pour les partitions avec effet de barrière
(Figure 6) où la division en deux républiques (B1)
a une qualité d’ajustement nettement meilleure que les suivantes
(B2 à B6). En effet, dès que l’on permute une ou plusieurs
régions pour les faire passer dans l’autre république, on
observe une chute très importante de la valeur du coefficient de
barrière et de la qualité d’ajustement. On peut donc affirmer
que dès la période 1961-65, la division en deux républiques
est incontestablement celle qui permet de constituer les entités
territoriales les plus intégrées sur le plan migratoire,
tout au moins par rapport aux contraintes qui ont été fixées
en ce qui concerne le nombre de classes et leur contrainte de contiguïté
.
Figure 4 : Qualité d'ajustement des modèles migratoires en fonction du choix de la partition (Tchécoslovaquie- 1961-65 ; 2 classes avec contrainte de contiguïté)
Figure 5 : Définition des 6 meilleures partitions associées à un effet de barrière (Tchécoslovaquie 1961-65 ; 2 classes ; contrainte de contiguïté)
Figure 6 : Détermination des 6 meilleures partitions associées
à un effet d'anti-barrière (Tchécoslovaquie 1961-65
; 2 classes ; contrainte de contiguïté)
Si l'on reprend le même protocole d’analyse pour la période 1986-90, on observe un bouleversement très important de la hiérarchie des partitions (Figure 7). En effet, la partition en deux républiques (B1) apparaît désormais nettement comme la partition optimale et son pouvoir explicatif est très nettement supérieure à l’ensemble des autres, qu’elles correspondent à des barrières ou des anti-barrières. L’augmentation de l’effet de barrière entre les deux républiques s’est donc accompagné d’une induration de la structure territoriale des échanges où, si l’on préfère d’une homogénéisation et d’une généralisation de l’effet de barrière qui exclue tout autre structure descriptive alternative. Par rapport au système descriptif adopté, la partition en deux républiques est incontestablement celle qui permet le mieux de rendre compte de l’organisation des échanges entre les dix régions de Tchécoslovaquie.
Figure 7 : Qualité d'ajustement des modèles migratoires en fonction du choix de la partition (Tchécoslovaquie 1986-90 ; 2 classes ; contrainte de contiguïté)
Il convient également d’ajouter que la méthode retenue
dans l’exemple précédent (examen exhaustif de l’ensemble
des partitions) n’est applicable actuellement qu’à des matrices
de migrations de tailles très réduites (25 x25). Mais le
programme de recherche que nous avons développé avec le LMC-IMAG
devrait bientôt permettre des applications sur des matrices de taille
beaucoup plus importante.
Le problème de la partition inconnue et l ‘étude de la dynamique des fragmentations territoriales
Si le problème de la partition inconnue possède une
incontestable " beauté mathématique " en raison de sa complexité
et du fait qu’il existe " au moins une solution ", il est également
du plus haut intérêt sur le plan empirique et sur le plan
théorique pour l’analyse géographique des fragmentations
socio-territoriales.
D’un point de vue empirique, tout d’abord, la recherche d’une partition optimale permet d’améliorer les modèles de prévisions puisqu’elle permet de déterminer la combinaison de paramètre qui donne l’ajustement le plus efficace compte tenu de l’information disponible. Après avoir déterminé la partition optimale sur un ensemble de périodes, on peut examiner l’évolution temporelle des paramètres correspondant d’interaction spatiale (a ) et d’interaction territoriale (g ) à différentes dates et essayer d’extrapoler les tendances de leur évolution. On a ainsi de fortes chances d’obtenir une prévision plus juste que celle qui aurait été réalisée à l’aide d’une simple analyse des variations de la mobilité générale et du frein de la distance. On peut également - mais c’est beaucoup plus compliqué - examiner l’évolution de la partition optimale à différentes dates et essayer d’analyser si son évolution obéit à certaines règles. En effet, un effet de barrière ne correspond pas nécessairement à une limite stable mais peut se déplacer selon un front de progression, certaines unités territoriales voyant leur appartenance se modifier ou s’inverser au cours du temps. Ainsi, dans le cas tchécoslovaque nous avons pu observer qu’il existait deux effets de barrières en 1961-65 (l’un entre la Bohême et la Moravie, l’autre entre la Moravie et la Slovaquie) qui se sont progressivement fondus en un seul à partir de 1970 (entre la république Tchèque et la Slovaquie). Nous avons également pu montrer dans le cas de la Belgique que les sous-provinces de Brabant-Nord et de Bruxelles qui faisaient office de zone-tampon au début des années 1960 se sont progressivement rattachées, l’une au domaine migratoire flamand et l’autre au domaine migratoire wallon.
Ceci nous amène à l’intérêt non plus empirique mais théorique du problème de la partition inconnue qui est de ne pas préjuger a priori de la forme et de la localisation des effets de barrière existant à l’intérieur d’un certain espace. En effet lorsque l’on adopte une démarche déductive (fixation d’une partition a priori), la modélisation tend souvent à conforter l’hypothèse initiale en montrant que la partition choisie correspond bien à un effet de barrière et fournit une bonne description du comportement des migrants. Mais ce résultat, s’il démontre que l’hypothèse retenue est acceptable, ne prouve pas que c’est la meilleure hypothèse possible. Il est donc nécessaire de valider l’hypothèse initiale (e.g. " les migrations en Tchécoslovaquie sont influencées par l’appartenance aux deux républiques tchèque et slovaque ") en comparant son pouvoir explicatif à celui d’hypothèses alternatives (e.g. " les migrations en Tchécoslovaquie sont influencées par l’appartenance aux trois régions historiques de Bohême, Moravie et Slovaquie "). L’intérêt central de la méthode de la partition inconnue est d’adopter une démarche inductive et de ne privilégier a priori aucune hypothèse quant à la localisation précise des barrières. Tout au plus doit-on spécifier quelles sont les contraintes retenues pour trouver la solution optimale (e.g. " quelle partition en deux classes territoriales contiguës influence le plus le comportement migratoire des populations en Tchécoslovaquie ").
Du coup, le problème de la partition inconnue suggère
une autre approche de la mesure des barrières qui consiste non pas
à déterminer un coefficient de réduction des échanges
mais à comparer le pouvoir explicatif de la meilleure partition
et des suivantes. En effet, on peut considérer qu’une structure
territoriale est d’autant plus pertinente qu’elle se démarque nettement
des autres structures territoriales susceptibles de rendre compte du même
phénomène.
4.3.4 Estimation d'effets de barrière complexes (interaction entre distance et appartenance territoriale)
L’amélioration théorique et méthodologique apportée par la famille des modèles d’interaction spatiale et territoriale multiplicatifs développés précédemment ne doit pas dissimuler le fait qu’il ne s’agit toujours que d’une solution particulière. En effet, le choix d’une forme multiplicative dans la modélisation des relations entre distance et appartenance est fondé sur un postulat d’homogénéité de l’effet de barrière. Plus précisément, la forme multiplicative présuppose que l’importance de l’effet de barrière est indépendante de la distance de relation. Par exemple, si l’on a trouvé que l’effet de barrière à une valeur moyenne de 2, on suppose que tous les flux franchissant une limite territoriale subissent en moyenne une réduction de moitié, qu’il s’agisse de flux à courte, moyenne ou longue distance. Or, rien n’indique que ce postulat soit vérifié. On peut au contraire imaginer que les personnes situés à très courte distance d’une frontière subissent moins l’effet de barrière car ils sont mieux informés de la situation dans la maille territoriale voisine, connaissent mieux sa langue, etc. Ainsi, le fait que beaucoup d’Alsaciens aillent travailler en Allemagne s’explique non seulement par leur proximité spatiale mais aussi par leur proximité culturelle et linguistique qui permet de lever un certain nombre d’obstacles. Toutefois, on pourrait imaginer des situations différentes où l’effet de barrière diminue avec la distance. Ainsi, dans le cas où une limite territoriale marque la trace d’un conflit entre les peuples situés de part et d’autres, on peut supposer que les facteurs psychologiques d’hostilité ou de méfiance réciproque sont davantage marqués à courte distance qu’à longue distance. Bref, on peut imaginer toutes sortes de théories qui conduisent à supposer que l’effet de barrière varie en fonction de la distance, quel que soit le sens de cette variation.Si tel est le cas, il convient de réviser nos hypothèses sur la forme multiplicative du modèle d’interaction géographique et de rechercher des formes plus complexes de relation entre la distance et l’appartenance. De plus, si l’effet de barrière varie en fonction de la distance, les mesures qui pourront en être faite vont subir fortement l’influence du niveau d’observation retenu (taille des unités spatiales) puisque la taille du maillage d’observation conduit à majorer ou au contraire à minorer l’importance des relations à courte distance par rapport aux relations à longue distance. De la même manière, les critères d’ajustement peuvent influer sur le calcul de l’effet de barrière si celui-ci varie en fonction de la distance. En effet, les différentes méthodes d’ajustement accordent un poids plus ou moins important aux flux en fonction de leur volume. Or, le volume est généralement corrélé avec la distance, les flux les plus important en volume se nouant en général entre des régions proches. Du coup, un changement de pondération correspond à un changement du poids relatif des relations à courte, moyenne ou longue distance dans l’évaluation des effets de distance et d’appartenance.
D’une manière générale, si l’on observe une instabilité
de l’effet de barrière en fonction du choix de la méthode
d’ajustement ou du choix du niveau d’observation, il y a de fortes chances
que cette instabilité soit liée à une variation de
l’effet de barrière en fonction de la distance, c’est-à-dire
à une hypothèse incorrecte sur le lien entre distance et
appartenance.
Définition d’un modèle général
Que l’on utilise un modèle gravitaire ou un modèle
à double contrainte le calcul d’un coefficient de barrière
unique dérive de l’hypothèse d’une relation simple entre
l’effet de la proximité spatiale et l’effet de la proximité
territoriale. Dans un modèle multiplicatif, les deux effets sont
combinés sous la forme d’un produit, ce qui revient à dire
que la fonction d’interaction géographique G
(effet combiné de la proximité spatiale et de la proximité
territoriale) est décomposable en deux termes indépendants
exprimant l’interaction spatiale S
et l’interaction territoriale T.
G(Dij, Aij) = S(Dij) . T(Aij)
Supposons maintenant que cette hypothèse ne soit pas vérifié, c’est-à-dire qu’il y ait une interaction entre la proximité spatiale et la proximité territoriale. Le nombre de modalités de la variable Aij étant fini, on peut exprimer la fonction d’interaction géographique comme la combinaison de fonction d’interaction spatiales particulières correspondant aux différentes modalités de Aij. Si on note A1..Az les différentes modalités de Aij et A1ij...Azij des variables booléennes prenant la valeur Akij=1 si Aij= Ak et Akij=0 si Akij ¹ Ak on peut écrire la fonction d’interaction géographique sous l’une des deux formes suivante :
G(Dij, Aij) = P k [Sk(Dij)]Akij
ou
G(Dij, Aij) = S k [Sk(Dij)]. Akij
Les différentes fonctions de la distance S1...Sz expriment le comportement spatial des migrants appartenant à chacune des classes d’appartenance territoriales A1..Az. Il y a donc a priori autant de fonctions d’interaction spatiales qu’il y a de types de proximité territoriale. Si l’on suppose qu’il existe un comportement moyen ou un comportement de référence S, alors on peut calculer pour chaque classe d’appartenance territoriale sa déviation par rapport au comportement moyen à l’aide de la fonction b k = Sk / S. La fonction b k exprime le comportement spatial spécifique des flux dont la classe d’appartenance territoriale est Ak. Le modèle d’interaction géographique peut alors s’écrire :
G(Dij, Aij) = S(Dij) . P k [b k(Dij)]Akij
Comportement spatial général & comportements spécifiques
Dans le cas particulier où l’on utilise une distance d’appartenance prenant les modalités Aij=0 (même appartenance) et Aij=1 (appartenance différente), on peut distinguer deux fonctions d’interaction spatiale S0 et S1 qui décrivent respectivement les flux intra-maille et les flux inter-mailles. La déviation relative des flux intra-mailles ou inter-mailles par rapport au comportement général est donnée par les fonctions b 0 =S0 /S et b 1 =S1 /S. On en déduit la fonction g = S0 /S1= b 0 /b 1 qui décrit la déviation des flux intra-mailles par rapport aux flux inter-mailles, c’est-à-dire la variation de l’effet de barrière en fonction de la distance. La fonction d’interaction géographiques correspondant à la présence d’un effet de barrière peut donc s’écrire sous l’une des trois formes équivalentes :
(A) G(Dij, Aij) = S(Dij) . [b 0(Dij)](1-Aij) . [b 1(Dij)](Aij)
(B) G(Dij, Aij) = [S 0(Dij)](1-Aij) . [S 1(Dij)](Aij)
(C) G(Dij, Aij)
=
[S 0(Dij)]
. [1/g
(Dij)](Aij)
Application du modèle général au cas des fonctions d’interaction spatiale de type Paréto
Nous partirons du modèle (B), c’est-à-dire de l’hypothèse
qu’il existe deux lois d’interaction spatiale f0(dij)
et f1(dij) décrivant respectivement
la décroissance des flux intra-maille et des flux inter-mailles
en fonction de la distance. On se place dans le cas d’un modèle
gravitaire sans contraintes, et on suppose que les deux fonctions d’interaction
spatiales obéissant à une loi de Paréto :
F0ij = k0. Ei . Rj . dij-a0 (relations intra-mailles)
F1ij = k1. Ei . Rj . dij-a1 (relations inter-mailles)
En transformant le modèle (B) en modèle (C), on en déduit une équation générale décivant le comportement de l’ensemble des relations intra-mailles ou inter-mailles :
Fij = k0. Ei. Rj . dija0. [(k1/k0). dij(a1-a0)] Aij
La fonction décrivant la variation de l’effet de barrière en fonction de la distance est donc :
g (Dij) = [(k1/k0). dij(a1-a0)]
Cette fonction n’est constante que si (a
1=a
0),
ce qui montre clairement que l’hypothèse d’un effet de barrière
homogène (indépendant de la distance parcourue) n’est valide
que si la vitesse de décroissance des interactions avec la distance
est la même pour les flux intra-maille et pour les flux inter-mailles.
Si la décroissance des interactions avec la distance est plus rapide
pour les flux inter-maille que pour les flux intra-maille (a
1
>a
0) l’effet de barrière
aura tendance à s’accroître avec la distance. Inversement,
si la décroissance des interactions avec la distance est plus rapide
pour les flux intra-mailles que pour les flux inter-mailles (a
1
< a
0), l’effet de barrière
aura tendance à diminuer avec la distance.
Si l’on définit maintenant X comme le logarithme de la distance, on peut montrer que le modèle de Paréto correspond à une fonction d’interaction spatiale définie par l’exponentiel d’un polynome P1(X) de degré 1.
Fij = k. Ei . Rj . dij-a
<=> Fij = Ei . Rj . exp [log(k) + a log(dij)]
<=> Fij = Ei . Rj . exp [P1(Xij)]
Si la décroissance des relations avec la distance obéit à une loi plus complexe que la loi de Paréto, on pourra tenter de l’approcher en recourant à une polynôme Pn(X) de degré n, le degré du polynôme étant fonction de la complexité de la fonction de décroissance des interactions en fonction de la distance. La détermination des fonctions d’interaction spatiales intra-maille et inter-mailles peut alors être entreprise par ajustement de deux polynômes P0n(X) et P1n(X) de paramètres respectifs (a00 ... a0n) et (a10 ... a1n) :
F0ij = Ei . Rj .exp [a00 + a01.log(dij) + a02.log2 (dij)+ ...a0n.logn(dij )] (relations intra-maille)
F1ij = Ei . Rj .exp [a10 + a11.log(dij) + a12.log2 (dij)+ ...a1n.logn(dij )] (relations inter-mailles)
Et le modèle général pourra s’écrire :
Fij = Ei . Aj . exp P0n(X) . [exp P1n(X) / exp P0n(X)]Aij
Il est alors facile de montrer que la fonction décrivant la variation de l’effet de barrière en fonction de la distance sera elle même l’exponentielle d’une fonction polynomiale de la distance de degré n
g (dij) = exp [(a10-a00)+ (a11-a01).log(dij) + (a12-a02).log2 (dij)+ ... (a1n-a0n).logn(dij )]
L’effet de barrière peut donc être non seulement variable
avec la distance, mais aussi présenter des minima et des maxima
si les degrés du polynôme supérieur ou égaux
à 2 ne sont pas nuls. Il convient toutefois de préciser que
les valeurs de l’effet de barrière ne sont significatives que sur
l’intervalle de distance commun aux flux intra-mailles et aux flux inter-mailles.
En effet si les flux intra-mailles sont connus sur l’intervalle [d0min
; d0max] et les flux inter-mailles sur l’intervalle
[d1min ; d1max], la fonction
g
(d) ne pourra être définie valablement que sur leur intervalle
commun. L’intervalle d’étude de g (d)
risque d’être encore plus réduit si l’on tient compte du fait
que son incertitude de mesure dépend à la fois de l’incertitude
d’estimation de la fonction d’interaction intra-maille et de celle de la
fonction d’interaction inter-mailles. Au total, il peut donc arriver que
l’estimation des variations de l’effet de barrière en fonction de
la distance soit impossible ou peu fiable car on ne dispose pas d’échantillons
suffisant de flux intra-mailles et de flux inter-mailles pour les mêmes
gammes de distance.
Typologie des variations de l’effet de barrière en fonction de la distance
L'analyse des paramètres du modèle polynomial suggère que, d'un point de vue théorique, on peut donc définir cinq grandes familles de situations en ce qui concerne la variation de l'effet de barrière en fonction de la distance. Si on note k le degré minimum du polynôme rendant compte de la variation de l'effet de barrière en fonction de la distance et g0, g1,...gk les paramètres de ce polynome on peut distinguer les cas suivants :
- (A) Barrière homogène (k=0 ; g0>1): le rythme de décroissance des interactions en fonction de la distance est le même pour les flux intra-maille et les flux inter-mailles. L’effet de barrière peut être résumé à l’aide d’une constante qui indique la réduction relative des flux traversant une limite territoriale par rapport à ceux qui restent à l’intérieur de la même maille territoriale.
- (B) Barrière croissante (k=1; g0>1; g1>0 ) : La décroissance des interactions en fonction de la distance est plus rapide pour les flux intra-mailles que pour les flux inter-mailles et l’effet de barrière tend à diminuer quant la distance augmente.
- (C) Barrière décroissante (k=1; g0>1; g1<0 ) : La décroissance des interactions en fonction de la distance est plus rapide pour les flux inter-mailles que pour les flux intra-mailles et l’effet de barrière tend à augmenter avec la distance
- (D) Barrière complexe (k>1; g0>1) : La fonction exprimant l’importance de l’effet de barrière en fonction de la distance présence au moins un minimum ou un maximum sur son domaine de définition. L’effet de barrière augmente ou diminue, selon les intervalles de distance considérés.
- (E) Barrière non-définie : Les flux intra-maille et inter-mailles sont définis sur des gammes de distance qui ne se recouvrent pas ou bien leur intersection ne comporte pas un échantillon suffisant de flux intra-maille et inter-mailles. L’effet de barrière ne peut donc pas être estimé, sauf en extrapolant les tendances observées pour les flux intra-mailles et inter-mailles.
Il va de soi qu'une typologie équivalente pourrait être
établie pour les anti-barrières en remplaçant
la condition g0>1
par
la condition g0<1
dans les expressions précédentes.
Figure 1 : Typologie des variations de l'effet de barrière
en fonction de la distance
Exemple d'application empirique : les migrations entre les provinces Belges en 1989
Partant d'un modèle gravitaire simple et sans contrainte,
on constate que les flux migratoires entre les provinces belges varient
en fonction de l'appartenance linguistique (Flandres / Wallonie+Bruxelles).
Mais la forme du graphique d'interaction suggère que l'effet de
barrière n'est pas indépendant de la distance parcourue par
les migrants.
On procède donc à un ajustement séparé des fonctions d'interaction spatiale décrivant le comportement migratoire intra-linguistique et inter-linguistique à l'aide d'un polynôme du logarithme de la distance. Les tests d'ajustement montrent qu'un polynôme de degré 2 assure un ajustement optimal pour les flux inter-linguistiques comme pour les flux intra-linguistiques (alors que le comportement général de l'ensemble du pays s'ajuste le mieux à un polynôme de degré 1, c'est-à-dire à une loi de Paréto classique).
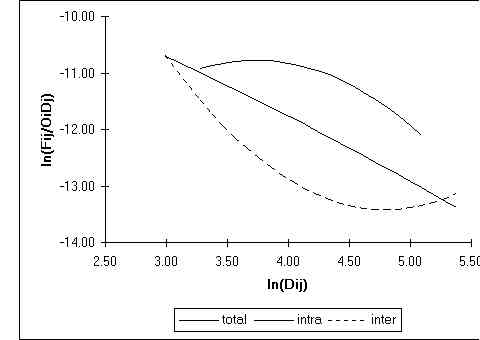
On déduit de l'équation des polynômes décrivant les comportements intra- et inter-linguistique la forme générale de la variation de l'effet de barrière en fonction de la distance.
Le graphique obtenu permet de montrer que l'effet de barrière varie très fortement en fonction de la distance. Faible pour les migrations à courte distance (division par 2 à 30 km) il culmine à moyenne distance (division par 9 à 75 km) et diminue ensuite régulièrement pour les distances les plus grandes (division par 3 à 160 km).
Plusieurs facteurs expliquent ces variations, notamment le rôle de l'agglomération bruxelloise située à cheval sur la limite linguistique (et qui favorise les transgressions de la limite linguistique à courte distance) ou celui des aires de villégiature situées aux extrémités opposées du pays (côte de la Mer du Nord en Flandres et région des Ardennes en Wallonie) et qui attirent des migrants de l'ensemble du pays à longue distance.
Mais la forme en cloche de l'effet de barrière observée en Belgique ne constitue pas un cas isolé et on l'observe également pour les migrations inter-républiques en Tchécoslovaquie ou pour les échanges internationaux de marchandise entre les régions de France et de Belgique.
Il semble exister certaines explications théoriques de portée générale permettant de rendre compte de la non-linéarité des effets de barrière et de l'apparition d'un maximum de l'effet de barrière à moyenne distance. Toutefois, leur discussion nécessiterait une discussion détaillée qui dépasse le cadre du présent exposé.
On se bornera donc à rappeler la fréquence de ce type
de situation et de mettre en garde l'utilisateur des modèles d'interaction
spatiale contre les formulations de l'effet de barrière multiplicative
simples, ne prenant pas en compte les variations possibles de l'effet de
barrière en fonction de la distance. Un simple graphique, du type
de celui que nous avons utilisé pour caractériser les interactions
en Belgique, suffit souvent à repérer le type de la relation
barrière-distance et permet de suggérer la forme de modélisation
la plus appropriée.
|
|