INTRODUCTION

Le quadruplet (x,y,z,t)

L'acte géographique élémentaire, le point de départ de toute démarche d'analyse spatiale, consiste à localiser des objets ou des événements à la surface de la Terre. Cet acte qui paraît anodin à l'heure des GPS a longtemps constitué une difficulté majeure puisque, si la mesure de la latitude a été obtenue très tôt avec une bonne approximation grâce au sextant, celle de la longitude posait des difficultés beaucoup plus redoutables (Cf. le roman d'U. Eco, L'île du jour d'avant). La difficulté de la mesure des longitudes était lié au fait que sa mesure dépendait d'un troisième paramètre de localisation, le temps. En effet la localisation d'un objet élémentaire à la surface de la Terre dépend d'un triplet (x,y,t) qui suppose l'existence d'un repère universel dans le temps et dans l'espace. Si l'on ajoute que la vie humaine ne se déroule pas sur une surface mais dans un volume qui possède une certaine épaisseur, il convient d'ajouter une dernière dimension qui est l'altitude (z). Au total c'est donc un quadruplet (x,y,z,t) qui permet de définir la localisation précise d'un objet ou d'un événement à la surface de la terre.
 

Points et lieux

Un second problème crucial pour la géographie est la distinction qu'il faut opérer entre points et lieux et les difficultés qu'entraîne l'assimilation des seconds aux premiers.

 Définition : un point de la surface terrestre est une position définie précisément par ses trois coordonnées de longitude, latitude et altitude. Un point est un objet abstrait de surface nulle.

Exemple :
- Le Pôle Nord : (90°00'N, ***, 0m)
- Le sommet du Mont Blanc : (46°55'N,6°52'E,4807m)

Définition : un lieu est une portion plus ou moins bien définie de la surface terrestre, de superficie non nulle, généralement dotée d'un nom propre.

Exemple :
- L'Arctique
- Le Massif du Mont-Blanc

Un lieu possédant une surface non nulle, il peut être caractérisé par différents attributs (surface, population, nombre d'entreprise, quantité de forêts, …) qui définissent son poids pour un critère donné.
 

- un point a une surface nulle alors qu'un lieu a une surface non nulle.
- un lieu peut contenir des objets alors qu'un point ne peut par définition rien contenir.
 

On classe souvent les lieux en points, lignes et aires. Il s'agit en fait d'une abstraction car tout lieu possède une superficie non nulle.
 

Des unités géographiques peuvent être assimilées à des points (ou des lignes) lorsque l'échelle d'observation l'autorise : pour une étude du système urbain français, on négligera la superficie des villes et chacune sera assimilée à un point correspondant au centre de gravité de la population ou de la superficie de la ville, voire à celui de sa commune-centre. De la même manière, une commune ou un département pourra être assimilée à un lieu, celui des coordonnées de son "chef-lieu" (qui comme son nom l'indique est le lieu de référence de l'unité spatiale).
 

Analyse d'un semis de points

Le point de départ de l'analyse consiste donc en un ensemble de N points 1..i..N décrits par leurs coordonnées de position (Xi, Yi, Zi, Ti). Dans ce chapitre, on négligera les différences d'altitudes (Zi) et on supposera que la situation observée correspond à la distribution à une même date (T), de sorte que l'on partira uniquement d'un tableau de coordonnées (X,Y).

On examinera toutefois le cas où le semis de point décrit un ensemble de lieux dotés d'une population P, de sorte que chaque lieu sera muni d'un poids Pi indiquant le nombre d'individus de la population P qu'il contient. Le tableau étudié sera alors du type (X,Y,P) et correspondra à la distribution d'une population

Situation absolue et situation relative

L'évaluation de la position d'un lieu peut se faire de deux façons différentes :

• soit en examinant sa localisation précise dans l'espace (situation absolue). On s'intéresse alors aux phénomènes localisés à proximité immédiate de ce lieu et on recherche quels facteurs endogènes expliquent l'évolution de ce lieu.
• soit en examinant la distance de ce lieux aux autres lieux (situation relative). On s'intéresse alors aux relations potentielles qu'il peut entretenir avec ces autres lieux et on recherche les facteurs exogènes qui expliquent son évolution.

D'une manière générale, les caractéristiques de situation absolue ont une portée explicative plus réduite que les caractéristiques de situation relative. Les premières expliquent les fondations initiales, mais au fur et à mesure que les échanges se développent, ce sont les caractéristiques de situation relative qui deviennent déterminantes.
 

A) INDICATEURS STATISTIQUES DE POSITION

A.1) Coordonnées et distances

Coordonnées géographiques et coordonnées planaires

- Les coordonnées absolues (on dit aussi géographique) correspondent à la localisation à la surface de l'ellipsoïde terrestre par le triplet (LONi,LATi,ALTi) :

• longitude : angle LONi entre le plan du méridien passant par ce point et le plan du méridien origine choisi (en degrés par rapport au méridien de Greenwich)
• latitude : angle LATi de sa normale -perpendiculaire à la tangente en ce point- avec le plan de l'équateur (en degrés par rapport à l'équateur, avec un signe + au Nord et - au Sud)
• altitude : élévation ALTi en m par rapport au niveau moyen de la mer

Dans la plupart des applications géographiques, on utilise des coordonnées planaires qui sont plus simples à obtenir (digitalisation d'une planche d'Atlas). Leur utilisation n'est pas gênante lorsque l'étude porte sur une petite portion de la surface terrestre, car celle-ci peut être localement assimilée à un plan. En revanche, si l'étude porte sur un grand espace, il faut être conscient des déformations entraînées par la projection.

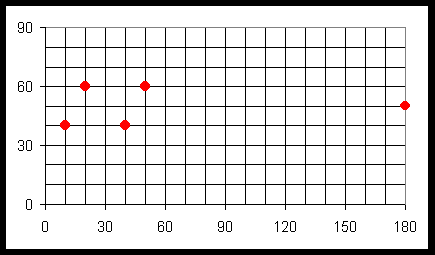
Exemple de tableau des coordonnées :
 

i	Xi	Yi
1	20	60
2	50	60
3	10	40
4	40	40
5	180	50

Transformation d'un tableau de coordonnées en matrice de distance

Les métriques sont des distances abstraites vérifient les quatre propriétés suivantes
 
 

1. non négativité : Dij >= 0
2. séparation : Dij=0 si et seulement si i=j
3. symétrie : Dij = Dji
4. inégalité triangulaire : Dik < Dij + Djk

Les métriques sont imparfaites, en ce sens qu'elles ne donnent que des approximations des distances empiriques que l'on souhaite mesurer. Mais elles ont l'immense avantage d'être beaucoup plus simple à calculer (elle ne dépendent que des coordonnées) et de pouvoir être appliqués à tous couples de points d'un espace. Ainsi, si l'on voulait mesurer la distance-temps entre 1000 lieux différents, il faudrait calculer 1 000 000 de valeurs. En recourant à une métrique, il suffit de connaître les coordonnées des 1000 lieux soit 2000 valeurs, auxquelles on applique chaque fois que nécessaire une fonction - généralement très simple.

La construction d'un grand nombre de métriques permet de choisir celle qui se rapproche le plus de la distance concrète que l'on veut étudier.
 

• Métrique euclidienne

Définition :

Exemple :

DEij	1	2	3	4	5
1	0	30	22	28	160
2	30	0	45	22	130
3	22	45	0	30	170
4	28	22	30	0	140
5	160	130	170	140	0

Propriétés :

• les points situés à une distance D d'un point O forment un cercle de centre O et de rayon D.
• la métrique euclidienne possède la propriété d'homogénéité : elle est invariable par translation
• la métrique euclidienne possède la propriété d'isotropie : elle est invariable par rotation.

Cette métrique postule que l'espace est homogène et isotrope. Elle introduit donc une simplification de l'espace géographique et ne serait parfaitement valable que pour les déplacements d'un patineur sur un terrain de hockey (pas d'obstacles, aucun itinéraire privilégié, aucune direction privilégiée, etc).

La métrique euclidienne correspond aux distances à vol d'oiseau ; elle sous estime les distances routières d'environ 15 à 30 % à l'intérieur d'un pays comme la France.

• Métrique rectilinéaire (distance de Manhattan)

Définition :

Exemple :

dRij	1	2	3	4	5
1	0	30	30	40	170
2	30	0	60	30	140
3	30	60	0	30	180
4	40	30	30	0	150
5	170	140	180	150	0

 Propriétés :

• les points situés à une distance rectilinéaire D d'un point O forment un losange à angles droit dont les sommets sont situés sur les axes Ox et Oy à une distance de D de O.
• la métrique rectilinéaire est homogène.
• La métrique rectilinéaire n'est pas isotrope : la distance entre deux points n'est pas modifiée par une translation mais elle l'est par une rotation.

• La métrique rectilinéaire est très utilisée dans les problèmes urbains lorsque le système de voies est plutôt orthogonal. Il faut cependant veiller à ce que les axes x et y du système de coordonnées correspondent aux directions principales de la voirie. Dans le cas contraire, il faut opérer au préalable un changement de repère pour mesurer les coordonnées des lieux.
• la métrique rectilinéaire facilite la résolution analytique de certains problèmes de localisation qui ne peuvent être résolus que de façon algorithmique avec la distance euclidienne (ex. recherche du point médian).

On peut construire des métriques oblilinéaires ou les deux axes de référence Ox et Oy ne sont pas orthogonaux. Cette solution est particulièrement intéressante lorsque l'on est en présence d'un réseau de transport organisé selon deux directions non orthogonales (ex. région des Appalaches).

• Les métriques centrales

métrique radiale

Elle correspond au cas où il est nécessaire de passer par le centre d'un réseau pour se déplacer d'un point à un autre qui n'est pas situé sur le même rayon.

Dr(i,j) = D(i,O) + D(O,j)

métrique périphérique

Elle correspond au cas où il faut éviter le centre et utiliser les voies périphériques. Si les deux points se situent sur des rayons différents il faut parcourir trois tronçons :

1) du point de départ au périphérique
2) sur le périphérique
3) du périphérique au point d'arrivée.

Dp(i,j) = D(i,P1) + D(P1,P2) + D(P2,j)

métrique circumradiale

En général on a la possibilité de choix entre métrique radiale et métrique périphérique. La métrique circumradiale consiste à choisir le minimum des deux solutions possibles.

Dc(i,j) = min [Dr(i,j) ; Dp(i,j) ]

Propriétés :

• Il n'y a ni homogénéité, ni isotropie. Le déplacement ou la rotation de deux points modifie la distance entre ceux-ci.

Ces métriques prennent en compte l'hétérogénéité de l'espace. Elles conviennent bien pour la mesure des distances à l'intérieur d'un espace polarisé par un centre organisateur.En Ile de France, le plus court chemin pour les transports en commun est associé à la métrique radiale alors que pour les transports individuels c'est souvent la métrique périphérique.

• métrique orthodromique

Définition :

La métrique orthodromique correspond à l'arc de cercle reliant deux points par le plus court chemin. Si on note (Aij) l'angle exprimé en radians que font ces deux points par rapport au centre de la Terre, la distance orthodromique est égale à

Dij = (Aij/3.1415) * 20000

On suppose que X est la longitude en degrés et Y la latitude en degrés :

Dij=6368*Arccos[(sin(Yi).sin(Yj))+(cos(Yi).cos(Yj).sin(Xi).sin(Xj))+cos(Xi).cos(Xj)]

Exemple :
 

Exemple : si on calcule le distances entre les villes européennes à l'aide d'une projection de Mercator, on va surestimer les distances entre les villes du Nord par rapport aux distances entre les villes du Sud : ex. Oslo (10°E,60°N) et Helsinki (25°E,60°N) et Prague (15°E,50°N) et Kiev (30°E, 50°N) Ces deux couples de villes semblent situés à la même distance sur une projection de Mercator (méridiens et parallèles perpendiculaires) car ils sont situés à la même latitude et avec une différence de longitude de 15°. Mais cette différence de longitude correspond à des distances différentes puisque le diamètre des parallèles se rétrécit : Prague-Kiev = 40000km*(15/360)*cos(50°) = 1071 km Oslo-Helsinki= 40000km*(15/360)*cos(60°) = 873 km

Propriétés :

Si l'on néglige l'aplatissement de la Terre aux pôles, cette métrique est à la fois homogène et isotrope.

Applications :

L'utilisation de cette métrique est obligatoire dès lors que l'on travaille sur de grands espaces pour lesquels une distance euclidienne appliquée à des coordonnées planaires pourrait entraîner des distorsions importantes.
 

A.2) Détermination d’un point central

Point moyen

Le point moyen non pondéré est le point G dont les coordonnées sont égales à la moyenne des coordonnées en X (mX) et la moyenne des coordonnées en Y (mY).
 

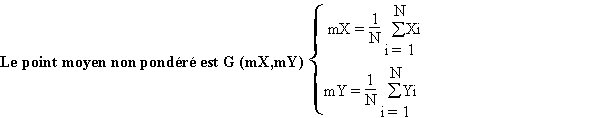
Son calcul est extrêmement simple et rapide, toutefois il possède deux limites fondamentales :

1. le calcul du point moyen n'a de sens que dans un référentiel euclidien.
2. Le point moyen ne correspond pas au point le plus accessible, c'est-à-dire à celui qui minimise la somme des distances à tous les autres.

Point moyen pondéré :

Lorsque l'on est en présence d'une distribution de population assimilée à un semis de points valués (X,Y,P), on peut calculer le point moyen pondéré Gp dont les coordonnées sont définies par les moyennes de X et de Y pondérées par P.
 

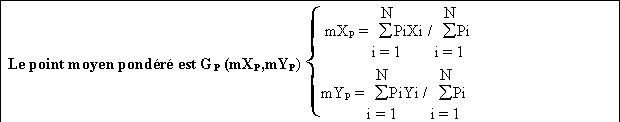
Là encore, le calcul est extrêmement simple, mais le point obtenu correspond au centre de gravité de la population et non pas au point le plus accessible pour l'ensemble des membres de la population P.

Applications :

Malgré ses limites, le point moyen a été beaucoup utilisé en géographie pour comparer entre elles les distributions de plusieurs phénomènes à une même date ou d'un même phénomène à différentes dates

Déplacement du point moyen de population en Iowa (1850-1970)

La colonisation de l'Iowa est facilement visualisée et l'on peut remarquer les périodes d'accélération ou de ralentissement du déplacement vers l'Ouest, ainsi que la croissance plus rapide de l'Est à partir de la seconde guerre mondiale. Source : Taylor P.J., 1977.

Calcul des centres de gravité de différentes productions en Ukraine vers 1926

Les géographes soviétiques prétendaient rationnaliser la production en s'efforçant de faire coïncider les différents centres de gravité de production et de consommation ... Après une éphémère heure de gloire, leur centre fut dissous car il proposait des solutions contradictoires avec la volonté du parti communiste ... Source : Taylor P.J., 1977.

Limites :

Le centre de gravité ne renseigne pas sur la dispersion des points ou de la population autour du centre de référence. Deux populations peuvent avoir un même centre de gravité mais être soit concentrées, soit dispersées autour de celui-ci.

Point médian

Point médian non pondéré :

Soit un ensemble de points 1..i..N distribués sur un espace E muni d'une métrique D, le point médian M est le point le plus accessible, c'est-à-dire celui qui minimise la somme des distances à l'ensemble de tous les points.
 
 

En règle générale, on ne peut trouver le point médian qu'en parcourant tout l'espace E et en calculant à chaque fois l'accessibilité jusqu'à ce qu'on trouve le point qui possède la meilleure accessibilité. C'est notamment le cas en distance euclidienne où il n'existe aucune formule mathématique simple permettant de déterminer le point médian.

Dans le cas particulier de la métrique rectilinéaire (mais dans ce cas seulement), le point médian est facile à déterminer puisqu'il correspond au point M dont les coordonnées sont égales à la médiane de X et à la médiane de Y.

Point médian pondéré :

Dans le cas d'une population P distribuée en N points 1..i..N de population P1..Pi..Pn, le point médian est celui qui minimise la somme des distances à l'ensemble de la population.
 
 

Comme dans le cas précédent, il n'existe pas de solution mathématique permettant de déterminer rapidement le point médian, sauf dans le cas particulier de la distance euclidienne où le point médian correspond aux médianes pondérées par P de X et de Y.

• La médiane pondérée de X est la coordonnée M(X,P) telle que la moitié de la population soit localisée à l'Est de M(X,P) et l'autre moitié à l'ouest.
• La médiane pondérée de Y est la coordonnée M(Y,P) telle que la moitié de la population soit localisée à l'Est de M(Y,P) et l'autre moitié à l'ouest.
• Le point médian pondéré est donc le point Mp qui découpe l'espace étudié en quatre quadrants rassemblant chacun 25% de la population totale.

Dans les problèmes d'aménagement du territoire ou de geomarketing, le point médian définit des localisations optimales au sens de la minimisation du coût moyen de transport ou de relation pour l'ensemble des habitants.

Un exemple célèbre d'application est le problème posé par l'économiste A. Weber pour la localisation d'une entreprise ayant recours à deux inputs et un output localisés en différents points de l'espace.

Limites :

Outre la difficulté de son calcul, le point médian possède un certain nombre d'inconvénients dans les situations réelles. Il n'est en effet pas toujours judicieux de localiser un équipement en rase campagne et l'on préférera souvent choisir une localisation existante plutôt qu'une localisation théorique.

Il arrive également que l'on cherche à localiser plusieurs équipements pour desservir une population , ce qui définit un problème de p-médiane : définir l'emplacement de p équipements minimisant la somme des distances des habitants à l'équipement le plus proche.
 

A.3) Dispersion autour d’un point central

Tout comme une valeur centrale est précisée par un paramètre de dispersion statistique, un point central doit être accompagné d'un paramètre de dispersion spatiale qui indique l'éloignement des points ou de la population par rapport à celui-ci. On utilisera des paramètres différents selon que l'on a retenu comme point central le point moyen ou le point médian.

• Distance-type / Point moyen

Formule de calcul :

Calcul non pondéré

Le paramètre de dispersion associé est la distance-type s_Dqui est la racine carré de la moyenne du carré des distances, c’est-à-dire la racine carrée de la somme des variances de X et de Y.
 

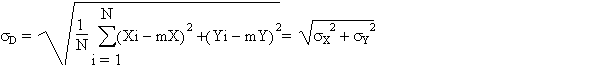Calcul pondéré

Le paramètre de dispersion associé est la distance-type pondérée s_D,P qui est égale à la racine carrée de la moyenne du carré des distances à tous les membres de la population P. Si on note s_X,P l’écart type de X pondéré par P et s_Y,P l’écart type de Y pondéré par P, on a :
 

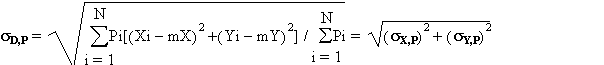Exemple d'application :

Evolution de la distance-type en Iowa (1850-1970)

Au fur et à mesure que la population colonise l'Iowa (déplacement vers l'Ouest), elle tend à se disperser de plus en plus sur l'ensemble du territoire de cet Etat. On remarque toutefois en 1970 que la dispersion n'est pas la même pour la population urbaine et la population rurale ou pour les jeunes et les vieux. La dispersion des surfaces (constante) donne une référence commode.  Source : Taylor P.J., 1977.

 

• Distance moyenne / point médian

Exemple : Si l'on étudie la distribution de la population mondiale à la surface de la terre en 1990 en distance orthodormique, le point le plus accessible est situé dans la haute vallée de l'Indus, aux confins du Cachemire et du Tibet. La distance moyenne à l'ensemble de la population mondiale y est de 5150 km.

• Quantiles d'accessibilité / Potentiels

D0% : distance minimum au point de référence
D50% : distance médiane permettant de totaliser 50 % de la population autour du point de référence
D100% : distance maximum au point de référence.

On verra dans la partie suivante que cette courbe cumulative d'accessibilité permet également de calculer des potentiels, c'est-à-dire des quantités de population en fonction de la distance au point de référence.
 

B) FORME DE REPARTITION DES DENSITES

B.1) Distribution des densités par rapport à un centre

Il arrive fréquemment qu'un semis de point présente une distribution concentrique avec une zone de concentration maximale autour de laquelle les densités décroissent plus ou moins rapidement. On peut alors chercher à modéliser la distribution à l'aide d'une courbe indiquant le gradient de densité à partir du point de concentration maximale.

Exemple théorique : distribution des cratères en fonction de la distance à un point chaud.

On constate que la densité de cratères diminue entre 0 et 3 km autour du point chaud. Au delà de cette distance, la distribution est uniforme et les cratères doivent être liés à des failles plutôt qu'à une chambre magmatique active.

 
 

• Population en fonction de la distance

On choisit ensuite une mesure de distance D permettant de calculer l'éloignement de tous les points 1..i..N par rapport au centre O. Cette distance peut être une métrique abstraite (euclidienne, rectilinéaire, …) ou une distance concrète (temps de transport, coût de transport, …).

On établit alors k classes de distances d'amplitudes égales[D0; D1]; [D1; D2[ ; … [Dk-1; Dk] qui permettent d'évaluer la quantité de population localisée dans chaque intervalle de distance par rapport au point de référence. Ceci permet d'établir un histogramme du nombre de point (ou de la quantité de population) en fonction de la distance P[Di; Di+1]

On en déduit une courbe cumulative Pcum(D) = P[0; D] exprimant la quantité cumulée de point (ou de population s'il s'agit d'un semis pondéré) en fonction de la distance.

• Surface en fonction de la distance

P(D) = k.D²

On va donc calculer parallèlement l'histogramme de la distribution des surfaces accessibles en fonction de la distance S[Di;Di+1] et la courbe cumulative correspondante Scum[D].

Dans un espace euclidien, cette surface est égale au disque de rayon D, mais il peut arriver que le calcul soit plus complexe parce que certaines surfaces ne peuvent pas accueillir de points (e.g. étendues inhabitables) ou parce que la distance utilisée n'est pas isotrope (e.g. surface définie par des isochrones qui s'étirent le long des axes routiers). .

• Gradient de densité

Dens [Di; Di+1] = P[Di; Di+1] / S[Di;Di+1]

On va alors chercher à résumer la courbe des densités en fonction de la distance à l'aide de la fonction la plus appropriée :
 

F(D) = Cste : densité uniforme F(D) = aD+b : fonction linéaire F(D) = exp(-aD+b) : fonction exponentielle F(D) = a. D-b : fonction puissance F(D) = a0 + a1.D +a2.D2 + … an.Dn : fonction polynomiale

 

• Exemple d'application : la loi de Clark

Les travaux de Clark portaient sur 36 villes à différentes dates. Ils ont montré que la loi exponentielle négative donnait dans la plupart des cas un excellent ajustement aux données empiriques, malgré quelques difficultés (cratère central de faible densité de population dans le CBD).Il a alors été possibles à ses successeurs d'étudier les variations du paramètre de la fonction de Clarke (densité centrale et gradient) et de montrer des variations selon la taille de la ville, l'ancienneté de l'urbanisation, etc. On a également calculé des gradients nonplus de densité de population mais de densité d'emploi, de services, etc.

Comme tout modèle, la loi de Clarke comporte des résidus qui apportent souvent des renseignements essentiels sur le phénomène étudié.

Ainsi, lorsqu'on applique la loi de Clarke sur la ville de Yaoundé, on observe une densité beaucoup plus faible que prévue dans le centre (même en tenant compte de l'effet cratère). Cette très faible densité du centre correspond à l'ancienne "ville blanche" de l'époque coloniale où les indigènes étaient exclus. Ceux-ci se sont installés à quelques kilomètres du centre dans des quartiers (Briquetterie, Mokolo, …) où la densité est vite devenue considérable. Après la décolonisation, le centre ne s'est pas densifié car il a été réutilisé par l'administration et le pouvoir politique pour y installer le CBD.
 
 

(a) Distribution de la population de Yaoundé en fonction de la distance au centre en 1987
 

Distance	Surface		Population en 1987		Densité
au centre (km)	km2	%	hab.	%	hab./km2	indice 100
[0;1[	3.8	1%	2700	0%	703	29
[1;1.5[	2.5	1%	28000	4%	11111	461
[1.5;2[	6.4	2%	84900	14%	13245	549
[2;2.5[	5.7	2%	74600	12%	12997	539
[2.5;3[	5.7	2%	67700	11%	11877	492
[3;3.5[	18.2	7%	144600	23%	7941	329
[3.5;4[	9.0	3%	57300	9%	6346	263
[4;4.5[	4.2	2%	20200	3%	4798	199
[4.5;5[	15.3	6%	36400	6%	2373	98
[5;5.5[	19.1	7%	37700	6%	1974	82
[5.5;6[	26.5	10%	27300	4%	1032	43
[6;6.5[	14.5	6%	10000	2%	690	29
[6.5;7[	26.8	10%	7600	1%	283	12
[7;7.5[	6.9	3%	1300	0%	190	8
[7.5;8[	3.3	1%	2700	0%	828	34
[8;8.5[	23.2	9%	9500	2%	410	17
[8.5;9[	9.6	4%	1200	0%	125	5
[9;9.5[	58.3	23%	11200	2%	192	8
Total	259.1	100%	624900	100%	2412	100

N.B. Les calculs sont effectués à l’aide du centroïde des chefferies : c’est pourquoi la croissance des surfaces n’est pas régulière.

(b) Forme de la décroissance de la densité de population en fonction de la distance au centre à Yaoundé en 1987
 

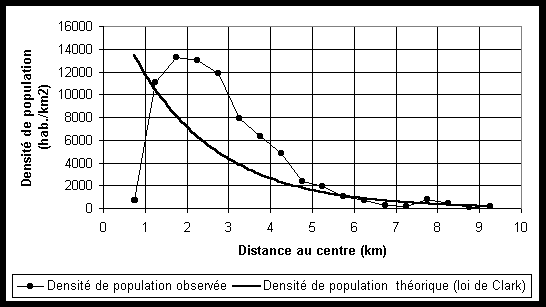
L'ajustement des données à la loi de Clark est très imparfait en raison de la forme très accentuée du cratère de basses densités du centre-ville. Le centre-ville correspond à l'ancienne ville "blanche", autrefois interdite aux autochtones, et toujours réservée actuellement aux bâtiments administratifs ou de prestige. Le pic de densité (vers 2 km) correspond aux anciens noyaux de peuplement indigènes de l'époque coloniale (Mokolo, Briquetterie, etc.).  Source : Bopda A., 1997, Yaoundé dans la construction nationale au Cameroun : territoire urbain et intégration, Thèse, Université Paris 1, 2 vol.;

 

B.2) Distribution des densités par rapport à un axe ou un réseau

Exemple théorique : localisation de nouveaux logements par rapport à une voie express

Dans cet exemple théorique, on suppose que l'on examine l'implantation des nouveaux logements dans une commune après l'arrivée d'une voie express. On constate que les habitants se localisent de préférence à 2-3 km pour bénéficier d'un bon accès à la voie express sans pour autant en subir les nuisances (courbe des densités en forme de cloche).

Les applications sont innombrables :

• Distribution de la population mondiale en fonction de la distance à la mer
• Distribution des espèces animales ou végétales en fonction de la distance aux cours d'eau
• Distribution des séismes en fonction des distances au lignes de fracture de l'écorce terrestre
• Etc.

B.3) Distribution des densités par rapport à une surface

On peut enfin calculer des distributions de densités sur l'ensemble d'une surface, sans utiliser des points d'appuis particulier grâce à la méthode des voisinages ou des fenêtres mobiles.

La méthode la plus simple est celle du cercle de rayon R que l'on promène en tout point i de l'espace d'étude pour déterminer le potentiel de population (quantité de population contenue dans le cercle de rayon R), le potentiel de surface (quantité d'espace contenue dans le cercle de rayon R) et la densité moyenne (rapport entre le potentiel de population et le potentiel de surface contenus dans le cercle) . On peut alors produire des cartes multiscalaires de densité qui seront plus ou moins généralisées selon le diamètre R du cercle qui aura été utilisé pour calculer les densités.

Pour en savoir plus :

Consulter le site "hypercarte"
Voir les exemples d'application en géographie du monde

Des méthodes beaucoup plus sophistiquées peuvent être développées pour étudier la répartition des densités dans l'espace (séries de Fourier, lissage gaussien, …) mais elles dépassent largement le cadre de cet enseignement d'initiation aux méthodes d'analyse spatiale.

C) ANALYSE DE LA FORME D’UNE DISTRIBUTION

Le choix qui est ainsi fait de privilégier la distribution uniforme peut être critiqué car pour beaucoup de phénomènes la distribution uniforme est totalement improbable (population, volcans, etc). On peut alors se demander l'intérêt qu'il y a à mesurer l'écart à un modèle dont on sait pertinemment qu'il n'est pas valide.

Le principe des deux méthodes qui vont être étudiées maintenant consiste précisément à ne pas fixer a priori la forme du modèle théorique correspondant à la distribution observée. On va chercher au contraire à déterminer, parmi plusieurs modèles théoriques possibles, celui qui s'ajuste le mieux à la distribution observée. Cette façon de procéder présente deux intérêts majeurs :

1) On passe du cadre de la simple description au cadre inférentiel. La réalisation d'un test permet de savoir si l'ajustement de notre distribution à une distribution théorique donnée est acceptable ou non pour un risque d'erreur donné. Les propositions initiales du type "La distribution est concentrée/aléatoire/régulière" sont falsifiables (au sens de K.R. POPPER - Cf. Chapitre 1).

2) Le fait de montrer l'adéquation entre la distribution observée et un modèle théorique permet de préciser des hypothèses sur la nature du phénomène qui a généré le semis de point.
 

C.1) Formes et processus générateurs des distributions

Adoptons une approche déductive et tentons de déterminer la forme d'une distribution en fonction du processus qui l'a engendré. On va considérer pour cela un espace composé de 16 carreaux de superficie égales (parcelles agricoles, blocs d'habitations, …) où l'on dénombre l'apparition d'objets ou d'événements qui se mettent en place de façon successive et non pas simultanée.

• Distribution régulière

• Forme générale : les densités sont aussi uniformes que le permet le nombre de quadrats et le nombre de points.

• urne : Un bon modèle de distribution concentrée est fournie par la distribution binomiale positive : on place K.N boules dans l'urne (N boules de chacune des K couleurs) et on effectue ensuite N tirages sans remise. Cela signifie qu'une couleur qui est sortie plusieurs fois aura moins de chances de sortir par la suite. La distribution sera donc plus régulière. On peut imaginer des variantes où non seulement la boule tirée n'est pas remise mais où, en plus, on en retire un certains nombre de la couleur qui vient d'être tirée.

• Processus générateur : l'implantation de nouvelle unités est d'autant plus probable que l'effectif est faible (ou la densité est la plus faible si les unités sont de superficie différente). Spatialement, cela aboutit a maximiser l'espacement entre les points, à occuper l'espace le plus régulièrement possible.

• Exemples en géographie : une distribution parfaitement régulière n'est possible que dans un espace homogène et avec une volonté politique coercitive s'appuyant sur une planification globale de l'espace. On peut songer à la distribution des fermes dans le Middle-West américain (espace homogène) appuyée sur le système du township. Toutefois la distribution n'est pas totalement régulière car, dès l'origine, il fallait tenir compte de l'inégal fertilité des sols, la taille des familles, etc. En outre, le système capitaliste a permis la concentration des terres et entraîné la disparition de beaucoup de petites exploitations, de sorte que le semis actuel des fermes est loin de la régularité. Plus généralement des problèmes de saturation de l'espace, de concurrence, etc aboutissent à des distributions régulières. La théorie des places centrales prévoit que les services ou les commerces de même niveaux tendent à se disposer de façon régulière dans l'espace (tout au moins lorsque la population est répartie de façon homogène).Le recours à l'ajustement d'une distribution binomiale peut donc s'avérer utile quand l'interprétation géographique d'un phénomène permet de penser que la localisation d'un point en un lieu décourage la localisation d'autres points dans ce même lieu.

• Distribution concentrée

• Forme générale : Dans la situation la plus extrême, tous les points sont localisés dans un seul carreau. Dans des formes plus atténuées, il y a opposition entre des carreaux saturés et des carreaux vides.

• urne : la distribution binomiale négative correspond à l'hypothèse inverse de la binomiale positive , c'est à dire l'existence d'une tendance à la concentration. En d'autres termes, la probabilité qu'un point se localise dans une maille augmente en fonction du nombre de points déjà localisés dans la même maille. Cela signifie que chaque fois qu'une boule d'une couleur a été tirée, on la remet dans l'urne et on en ajoute plusieurs de cette couleur (ou l'on retire celles qui sont de couleurs différentes). Les distributions engendrées par ce processus seront donc plus concentrées que celles qui seraient générées par un processus aléatoire.

• Processus générateur : l'implantation d'une nouvelle unité a plus de chances de se produire dans les carreaux ou l'effectif est le plus fort (ceux ou la densité est la plus forte si les unités sont de superficie différente). Le processus n'est pas aléatoire puisque, de façon cumulative, les premières localisations choisies deviennent de plus en plus attractive. Dans le cas extrême, la seule marge de liberté est l'implantation du premier point, tous les autres se localisant ensuite dans le même carreau. Spatialement, cela aboutit à minimiser le plus possible l'espacement entre les points.

• Exemples en géographie : La localisation des ministères peut correspondre à ce type de distribution dans la mesure où ceux-ci ont besoin de proximité pour échanger leurs informations. A partir du moment ou le premier point est choisi (siège de la capitale où réside le premier ministre), les autres ministères s'implantent à proximité. Un exemple actuel est celui du changement de capitale en Allemagne réunifiée. Les ministères vont progressivement se concentrer à Berlin. La loi binomiale négative est donc adapté aux distributions concentrés où l'on soupçonne qu'un processus d'agglomération est à l'oeuvre. Ce cas est très fréquent en géographie en raison de l'existence d'économies d'échelles et d'économie d'agglomération. Les entreprises tendent à se regrouper pour diminuer leurs externalités (routes, infrastructures, ...) et profiter de services communs

• Distribution aléatoire

• forme générale : une distribution est la réalisation d'un processus purement aléatoire si elle remplit deux conditions :

1. chaque carreau a une probabilité égale de contenir des points ; chaque point a une probabilité égale d'être localisé dans un quadrat quelconque.
2. la localisation d'un point est indépendante de celle des autres points.

• urne : on place K boules dans l'urne. A chaque fois on en tire une, puis on la remet. A chaque tirage, toutes les boules ont la même chance de sortir.

• Forme mathématique :

m : nombre total de points distribués dans l'ensemble observé.

d = m/n : probabilité qu'un point tombe dans un carré donné.

Px : probabilité qu'un carré compte x points

Px = e-d.dx /(x!)

e = 2.71828 est la base du logarithme néperien

Exemple :

Soit un espace comportant 48 points, divisé en  16 carrés => d=3 - la probabilité qu'un carré comporte 0 points est de 5.0% - la probabilité qu'un carré comporte 1 points est de 14.9% - la probabilité qu'un carré comporte 2 points est de 22.4% - la probabilité qu'un carré comporte 3 points est de 22.4% - la probabilité qu'un carré comporte 4 points est de 16.8% - la probabilité qu'un carré comporte 5 points est de 10.1% - la probabilité qu'un carré comporte 6 points est de 5.0% - la probabilité qu'un carré comporte 7 points est de 2.2% - la probabilité qu'un carré comporte 8 points est de 0.8% - la probabilité qu'un carré comporte plus de 8 points est de 0.4%

• propriétés de la distribution de Poisson :

Un indice simple permettant de déterminer si l'on est en présence d'une distribution aléatoire consiste à comparer la moyenne et la variance des densités en calculant le rapport varaiance/moyenne :

Signification du rapport variance/moyenne

V(d)/d = 1 : distribution aléatoire V(d)/d > 1 : tendance à la concentration V(d)/d <1 : tendance à la dispersion

• Processus générateur : La distribution de Poisson est intéressante lorsque l'on est en présence d'un processus où la probabilité de localisation d'un point dans une unité est indifférente à la localisation d' autres points dans cette zone. Elle traduit :

• soit le hasard
• soit un processus complexe ou des causes nombreuses agissent en sens divers et exercent chacune une action faible.

• Exemples en géographie : Beaucoup de recherches médicales étudient la distribution de maladies rares dans l'espace (leucémies, cancers, etc). Pour éliminer l'effet de masse, on raisonne à population égale pour que chaque lieu ait théoriquement le même nombre de points. Ensuite, on examine si la répartition des points est aléatoire dans l'espace. Si elle ne l'est pas, il est probable que des causes spatiales interviennent et il faut les identifier.

C.2) Test de la forme d’une distribution

Tester la forme d'une distribution revient à poser l'hypothèse que celle-ci est le résultat d'un processus d'un certain type (aléatoire, concentration, dispersion) et à confronter la distribution observée à une distribution théorique correspondant à l'hypothèse choisie. Les distributions binomiales positive et négative étant relativement complexe, on se limitera dans le cadre de cet enseignement à confronter les distributions observées à une distribution aléatoire (distribution de Poisson). On partira donc à chaque fois de l'hypothèse nulle :

H0 : la distribution observée est le résultat d'un processus aléatoire

Si H0 est rejetée, cela signifiera qu'il existe une tendance significative à la concentration ou à la dispersion des points.

Méthode des quadrats

(1) Dénombrement

Distribution des églises et chapelles du Comté de Leicester
 

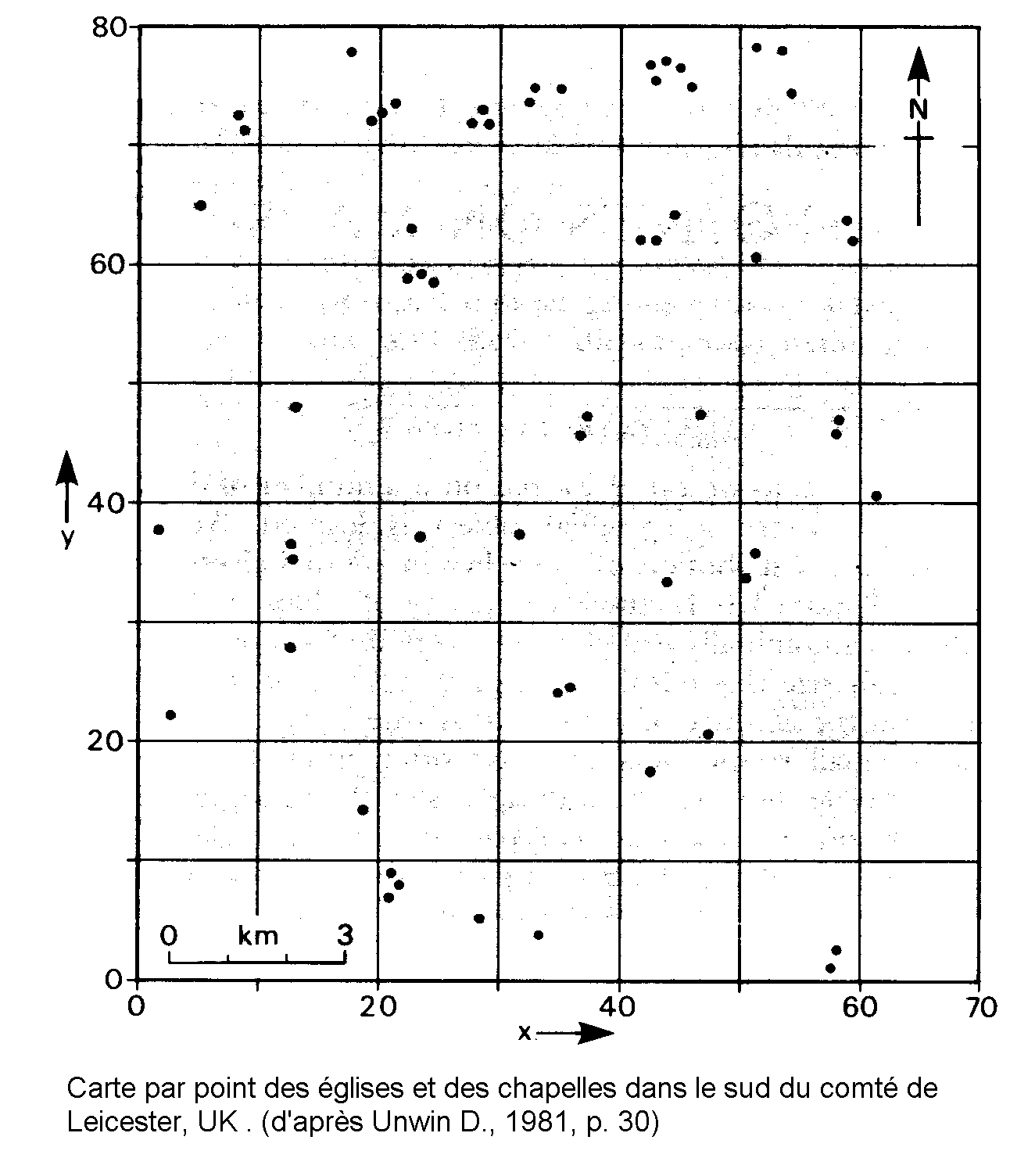Dénombrement de la fréquence des Eglises par carré de 10 km de côté

points	quadrats	points
n	K	n.K	(n-D)	K(n - D)2
0	25	0	-1.071	28.676
1	15	15	-0.071	0.076
2	8	16	0.929	6.904
3	5	15	1.929	18.605
4	1	4	2.929	8.579
5	2	10	3.929	30.874
Total	56	60		93.714
Densité moyenne D = nb. de points / nb. de quadrats = 60/56 = 1.071
Variance V(D) = 93.714 / 55 = 1.704
Indice de concentration IC = V(D)/D= 1.590

(2) Calcul de l'indice de concentration

La seconde étape de l'analyse consiste à examiner la forme de la distribution des fréquences de points par carreaux et à déterminer si elle se rapproche plutôt d'une distribution aléatoire, concentrée ou régulière. Pour cela, on dispose d'un indice très simple qui est le rapport entre la densité moyenne de points par carreaux (D) et la variance de cette densité V(D). On sait en effet (Cf. supra) que le rapport variance/densité tend vers 1 dans le cas d'une distribution aléatoire.

Dans l'exemple des chapelles du comté de Leicester, ce rapport est de 1.59 ce qui signale une tendance assez marquée à la concentration des chapelles en certains points du territoire. La variance est en effet élevée parce qu'il y a quelques carreaux très plein et beaucoup de carreaux vides.
 

(3) Détermination de la distribution théorique des fréquences par carreau

 
On va alors reconstituer ce que serait la distribution la plus probable des fréquences si la distribution était aléatoire. Pour cela, on utilise les fréquences théoriques déduites de la loi de Poisson :
 


 

Exemple : Sachant que la densité moyenne est D=1.071 points par carreaux, on peut déterminer la probabilité qu'un point contienne 0 points (34.3%) et en déduire le nombre théorique de carreaux devant contenir 0 points (56 * 0.343 = 19.2).

Ces calculs sont effectués pour toutes les fréquences observées, la probabilité ou la fréquence de la dernière classe (3 et + ) étant déduite par soustraction.

Fréquences observées et théoriques du nombre de chapelles par carreau
 

n	Observé	Théorique	(O-E)
0	25	19.2	+5.8
1	15	20.6	-5.6
2	8	11.0	-3.0
3 et +	8	5.2	+2.8
Total	56	56	0

Confirmant les observations précédentes, on remarque qu'il y a un excédent de carrés plein (3 et +) ou vide (0) et un déficit de carrés contenant un nombre moyen de chapelles (1 ou 2). Ceci est typique d'une distribution concentrée.

Il serait toutefois imprudent d'en conclure immédiatement que la distribution n'est pas aléatoire, car la situation théorique ne constitue que la distribution la plus probable d'un processus aléatoire. Le hasard peut très bien engendrer de temps à autre des distributions plus ou moins fortement concentrée. Il convient donc de déterminer si la distribution observée correspond à une simple fluctuation autour de la distribution la plus probable ou bien si elle révèle une distribution rare qui aurait normalement très peu de chances d'apparaître si les églises se localisaient au hasard. Pour trancher, on va recourir à un test statistique (test du Chi-2) permettant d'évaluer la significativité de la déviation observée entre les distributions observées et théoriques.

Calcul du Chi-2 de l'écart entre fréquences observées et théoriques des chapelles

n	Observé	Théorique	(O-E)2/E
0	25	19.2	1.762
1	15	20.6	1.502
2	8	11.0	0.823
3 et +	8	5.2	1.444
Total	56	56	5.531

Dans l'exemple des chapelles, on obtient un Chi-2 de 5.531 pour 3 degrés de liberté (nombre de classes moins une). Or, l'analyse de la table des valeurs théoriques du Chi-2 pour 3 degrés de liberté montre que cette déviation n'a rien d'exceptionnel :

Extrait de la table du Chi-2

Chi2 (3, 0.01) = 11.34

Chi2 (3, 0.05) = 7.82

Chi2 (3, 0.10) = 6.25

Chi2 (3,0.20) = 4.64

Les déviations observées ont entre 10% et 20% de chances de se produire dans le cas d'une distribution aléatoire, ce qui signifie qu'on aurait 10 à 20% de chances de se tromper si l'on affirmait que la distribution observée n'est pas aléatoire. Sachant qu'en sciences sociales on se fixe généralement un seuil de décision de 5%, on doit conclure ici que "la distribution observée n'est pas significativement différente d'une distribution aléatoire". Cela ne signifie pas que les chapelles se soient disposées au hasard, car la loi de Poisson peut être le résultat de causes multiples agissant dans des directions différentes. Mais en tout état de cause on ne peut pas affirmer que les chapelles aient eu tendances à se regrouper ou se disperser en certains points du comté de Leicester.
 

Il convient de remarquer que la méthode des quadrats n'est pas exempte de faiblesse. Le choix de la taille et de la forme des carreaux peut en effet entraîner des conclusions différentes pour une même distribution. Ceci peut dans certains cas révéler des problèmes d'échelle, une distribution pouvant être concentrée à l'échelle locale et dispersée aux échelles supérieures (ou l'inverse).

Pour une discussion plus approfondie de ce point, Cf. Taylor P.J., 1977, pp. 146-149.

Méthode du plus proche voisin

(1) Principe général de la méthode du plus proche voisin

(a) Soit un semis de N points distribués sur un espace de surface S. On note d la densité moyenne de points par unité de surface à l’intérieur de l’espace considéré (d=N/S)

(b) On calcule pour chaque point i la distance D_min(i) qui le sépare de son voisin le plus proche.

(c) On calcule ensuite la moyenne des distances observées au plus proche voisin D_O

(d) On détermine la distance théorique moyenne au plus proche voisin D_T dans le cas d’une distribution aléatoire à l’aide de la formule :

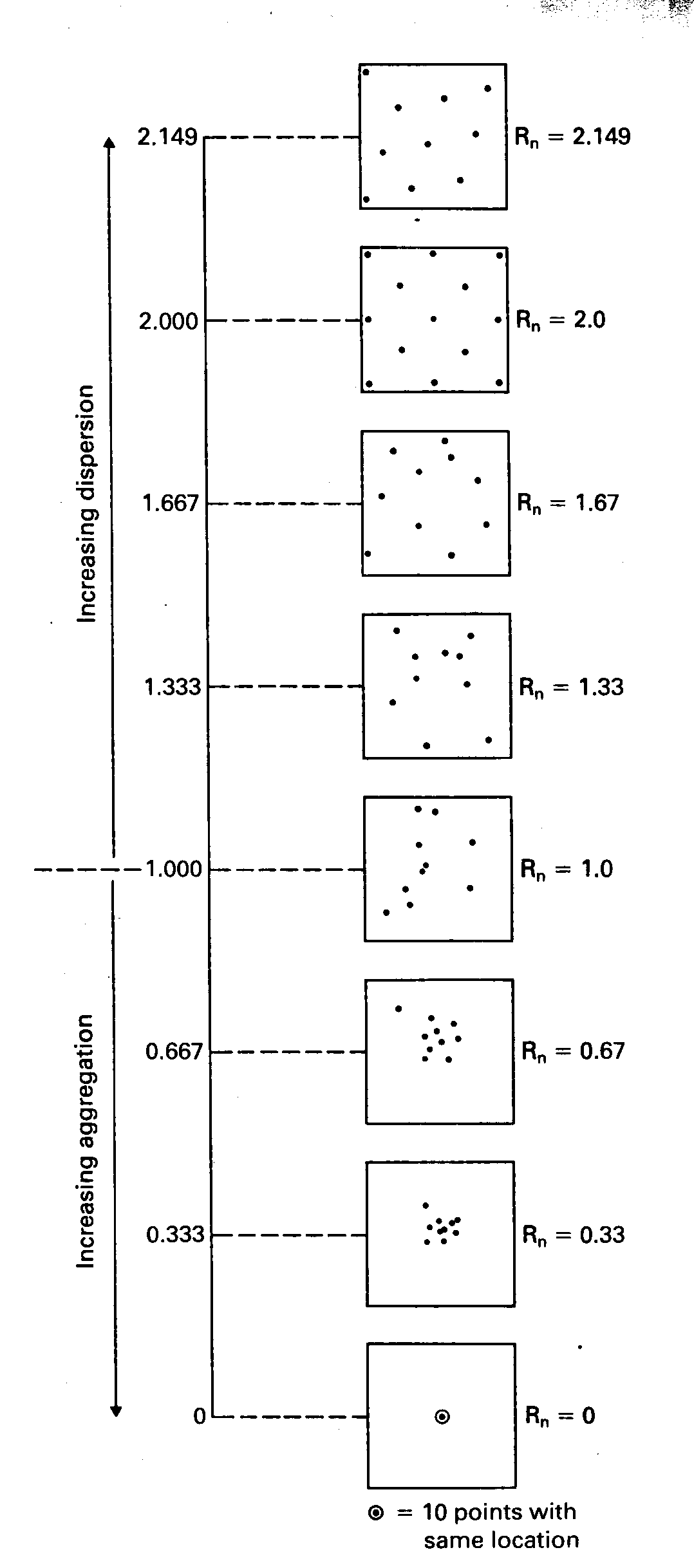
( e) On calcule l’indice de dispersion qui est le rapport entre ces deux distances :

R=D_O/D_T

La valeur de cet indice permet de se faire une idée de la forme de la distribution, sachant qu'il varie entre 0 (concentration totale) et 2.149 (dispersion maximale selon une grille hexagonale).
 
 

(f) Enfin, on peut tester le caractère aléatoire de la distribution à l’aide d’un test paramétrique qui dépasse le cadre de la licence mais peut être trouvé dans tous les (bons) manuels d'analyse spatiale

(2) Exemple d'analyse du plus proche voisin (données théoriques)
 
 

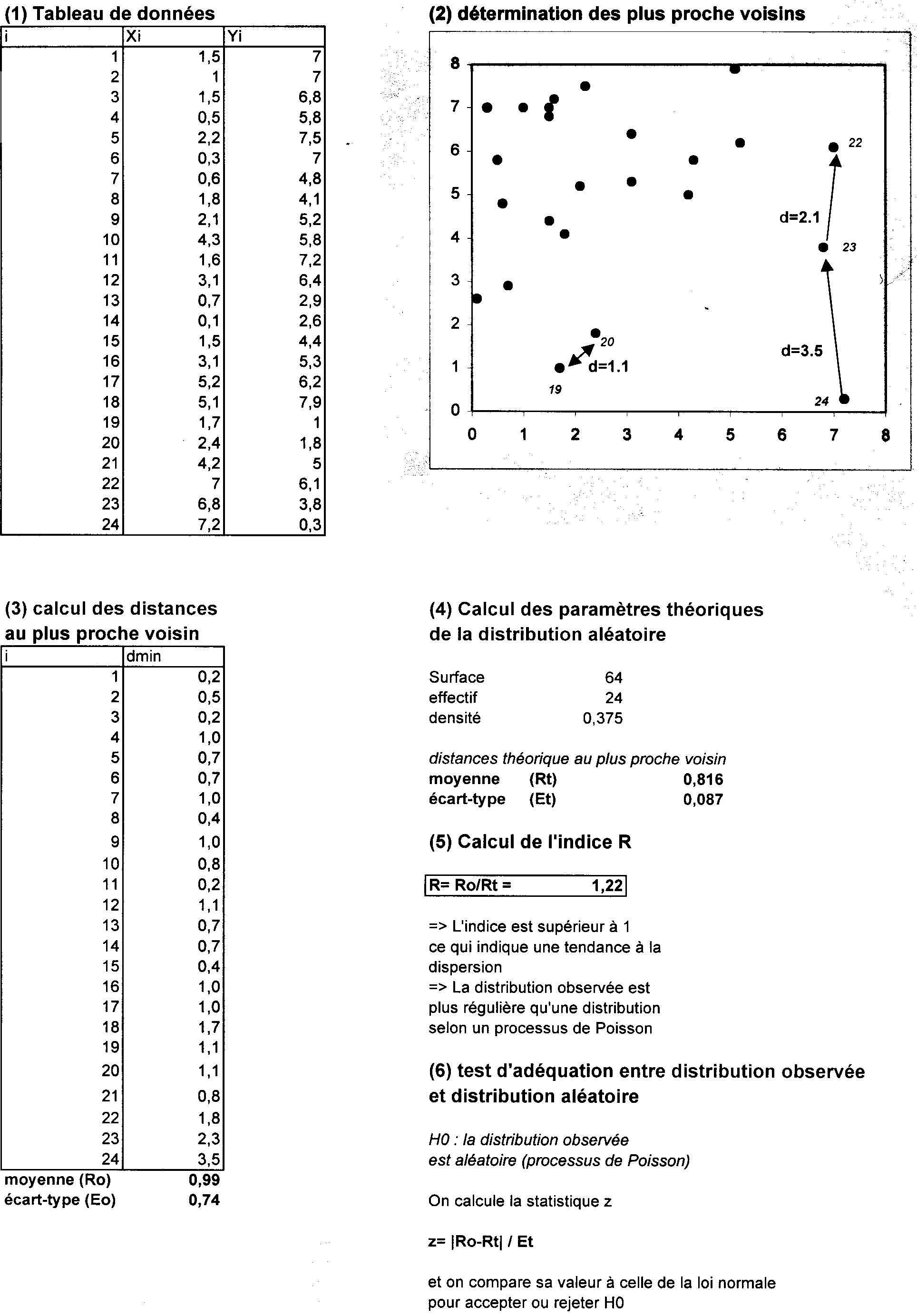(3) Critique de la méthode du plus proche voisin

Tout comme la méthode des quadrats, la méthode du plus proche voisin possède un certain nombre de défauts et de limites, qui peuvent être partiellement résolus.

• effets de bordure : Lorsque l'espace d'étude est délimité de façon arbitraire, on risque de surestimer la distance au plus proche voisin des points situés en périphérie, car leur plus proche voisin peut se situer en dehors de la zone d'étude. Ce problème peut être résolu en ajoutant une zone "buffer", un couloir autour de la zone d'étude où les points sont relevés mais pas utilisés dans l'analyse.
• effets d'échelle : Il peut arriver que des agrégations se produisent à un niveau, par exemple lorsque les points vont 2 par 2 (couples d'amoureux sur une plage) ce qui va engendrer une impression de concentration qui serait démentie à une autre échelle (les couples d'amoureux sont dispersés sur la plage). On peut résoudre ce problème en complétant l'analyse du plus proche voisin par l'analyse de la distance aux 2^e, 3^e, 4^e … voisins.

CONCLUSION

Malgré leur caractère relativement abstrait, les méthodes d'analyse des semis de points constituent un élément essentiel de toute démarche d'analyse spatiale et beaucoup de méthodes qui seront vues par la suite (analyse de réseaux, de surfaces, de diffusion, …) ne peuvent être pleinement comprise que si l'on a parfaitement intégré les notions de ce premier chapitre.

Quant aux difficultés proprement statistique (test d'une distribution aléatoire) elles ont été volontairement simplifiées, mais l'étudiant aura tout intérêt à les approfondir par lui-même car elles sont la base d'une approche scientifique des formes spatiales. Ainsi, c'est en recourant à des tests statistiques très poussés que le géographe S. Oppenshaw a pu démontrer le caractère dangereux de la centrale nucléaire de Sellafield (concentration anormale de Leucémie) contre l'opinion rassurante du ministère britannique de la santé. Il a même découvert au cours de ses recherches un foyer épidémiologique dangereux dont tout le monde ignorait l'existence (incinérateur fonctionnant à trop basse température et libérant de la dioxine).

• Pour plus de détails sur cet exemple, Cf. Gould P., 1992, "Epidémiologie et Maladie", in Bailly A., Ferras R., Pumain D. , Encyclopédie de Géographie, Economica, pp. 958-959