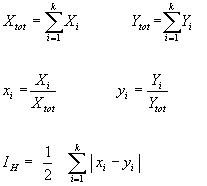1.1 LES MESURES D'EQUIREPARTITION
Un grand nombre d'indices dits de "concentration spatiale"
sont en fait des indicateurs généraux d'équirépartition
entre deux populations (X,Y) distribuées à l'intérieur
d'un même ensemble de mailles (M). Si l'on note k le nombre
de mailles, X1...Xk et Y1...Yk
la fréquence d'apparition des populations X et Y dans
chacune des mailles et Z1...Zk la densité
de X par rapport à Y dans chacune des mailles (Zi
=
Xi/Yi), on peut montrer que la plupart de ces
indices visent à mesurer l'écart entre la distribution observée
et une distribution théorique d'équirépartition où
Z1=Z2=...Zk.
1.1.1 Deux indices d'équirépartition
Parmi beaucoup d'autres, on peut signaler les indices de Hoover
et de Gini qui sont sans doute les plus fréquemment utiliser pour
mesurer l'équirépartition de deux populations à l'intérieur
d'un maillage.
Indice de Hoover
L'indice de Hoover (aussi appelé indice de différenciation)
exprime la part de la population X (ou de la population Y) qu'il faudrait
déplacer d'une maille à une autre pour aboutir à l'équirépartition.
Il varie entre 0 (équirépartition parfaite) et 1 (concentration
maximale qui ne peut être atteinte que si les populations X et Y
n'apparaissent jamais dans les mêmes mailles).
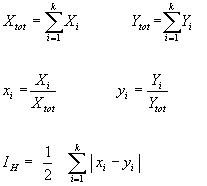
Indice de Gini
Très proche de l'indice de Hoover, l'indice de Gini permet
de compléter la mesure de l'équirépartition par une
courbe de concentration qui permet de préciser la forme des inégalités
de répartition de Y par rapport à X. Son calcul n'est toutefois
possible que si la valeur de la population X est non nulle dans chacune
des mailles.

1.1.2 Exemple de calcul des indices de Gini et de Hoover
Résoudre l'exercice 1 en
calculant les indices de Gini et de Hoover dans chacune des situations
A,
B,
C,
D
en utilisant tantôt le maillage des
cellules,
tantôt celui des quartiers
1.1.3 Discussion des résultats
-
Les indices d'équirépartition sont totalement indifférents
à la position relative des mailles territoriales dans l'espace (comparaison
des situations B,C,D). Le fait que les mailles à forte densité
de population soit proches ou éloignées les unes des autres
n'a aucune incidence sur la valeur prise par les indices.
-
Les indices d'équirépartition sont très sensibles
au choix du niveau d'agrégation c'est-à-dire à la
taille et la forme des mailles territoriales utilisées pour les
calculer (comparaison des indices calculés par cellules ou par quartier).
-
Les indices d'équirépartition font jouer un rôle symétrique
à la population et à la superficie alors qu'il existe en
géographie une dissymétrie fondamentale du couple population-société.
-
Dans la mesure où les indices dépendent fortement du choix
de la maille, ils expriment davantage la concentration territoriale du
peuplement que sa concentration spatiale.
-
Plus précisément, ils expriment l'inégale disponibilité
d'espace par habitants en faisant l'hypothèse implicite que chaque
communauté d'habitant (personnes localisées dans une même
maille) se partage l'espace disponible de façon égalitaire.
Le concept sous-jacent à l'application des indices d'équirépartition
en géographie est donc celui de l'appropriation de l'espace par
des groupes territorialisés.
L'exemple le plus probant d'application de ces indices serait celui
de la répartition de la terre entre des communautés d'agriculteurs
pratiquant un partage égalitaire des ressources. Les mailles correspondent
alors aux communautés d'agriculteurs, la surface à la quantité
de terre dont dispose la communauté et la population aux nombre
de membres de la communauté (familles ou personnes). L'indice exprimerait
alors le degré de concentration de la ressource foncière
entre les membres des différentes communautés qui composent
une société en faisant abstraction des inégalités
qui peuvent exister à l'intérieur de chaque communauté.