1.3 LES MESURES DE CONCENTRATION SPATIALE
Dans la pratique, la mobilité des individus rend la connaissance de ces positions impossible et la seule information disponible est la localisation résidentielle des habitants au moment du recensement, c'est-à-dire leur affectation au temps t à une certaine maille territoriale Mi . On suppose que le maillage M {M1..Mk}définit une partition exhaustive de l'espace géographique E au temps t, ce qui signifie qu'il exsite une application m qui associe à toute position spatiable zi,t pouvant être occupée par un individu au temps t sa position territoriale mi,t qui désigne l'une des k mailles territoriales M1..Mk .
On associe enfin à chaque maille territoriale un ensemble d'attributs Zi,t {Xi,t, Yi,t , Pi,t ,Si,t} qui décrivent respectivement la position spatiale moyenne des individus à l'intérieur de celle-ci (X,Y), le nombre d'individus localisés à l'intérieur de celle-ci (P) et le nombre maximum de positions disponibles à l'intérieur de celle-ci (S). Ces informations n'étant pas nécessairement disponibles, on utilisera des estimations telles que la surface (S*), la population au lieu de recensement (P*), et le centre géométrique (X*,Y*) de la surface définie par l'enveloppe territoriale des mailles.
En résumé, la nature agrégée de l'information et la mobilité humaine ne permettent pas de connaître directement les positions spatiales des individus et celles-ci ne sont connues que par l'entremise d'un outil d'observation (le recensement) fondé sur un critère (le lieu de domicile) et une grille (le maillage) qui ne peuvent fournir que des approximations des positions réelles, approximation entâchées d'une certaine incertitude.
Cette formalisation très lourde d'une information apparemment
aussi simple que la population et la superficie d'un ensemble d'unités
spatiales est en réalité indispensable pour comprendre la
signification sociale des mesures d'accessibilité spatiale qui pourront
en être déduite et pour estimer l'erreur de mesure sur les
paramètres d'accessibilité lorsque l'information n'est pas
connue au niveau des individus mais à celui d'agrégats territoriaux
(situation la plus fréquente en géographie).
1.3.1 Calcul de la distance moyenne entre deux habitants
Considérons en effet deux mailles territoriales Mi et Mj de superficie respectives Si et Sj et de population Pi et Pj et notons respectivement dminij et dmaxij la distance minimum et la distance maximum entre les points les plus proches et les plus éloignés de chacun des deux polygones. On peut affirmer sans risque d'erreur que les (Pi x Pj) couples d'habitant localisés respectivement dans les deux mailles territoriales sont éloignés de distances comprises dans l'intervalle [dminij ; dmaxij]. Quel que soit l'estimateur de distance moyenne retenu pour mesurer la distance moyenne des habitants de i et j, l'incertitude de mesure est donc bornée par une valeur maximale qui sera d'autant plus faible que les mailles sont de faible superficie. On peut d'ailleurs ajouter que l'incertitude de mesure sur la distance entre les habitants de l'ensemble du système sera en moyenne beaucoup plus réduite que celle d'une maille quelconque car la structure bi-dimensionnelle de l'espace introduit des compensations entre les erreurs d'estimations des distances intermailles. En effet si le point moyen censé représenté le centre de gravité de la population d'une maille i (Xi,Yi) est localisé trop à l'ouest, ceci va entraîner une surestimation des distances réelles entre ses habitants et ceux qui sont localisés dans des mailles localisées plus à l'est, mais aussi une sous-estimation des distances réelles avec les habitants des mailles situés plus à l'ouest. Au total, les deux effets ont de fortes chances de se compenser, sauf pour les mailles les plus périphériques.
La difficulté principale réside en fait dans l'estimation des distances moyennes entre les habitants d'une même maille territoriale, pour lesquelles on ne dispose a priori d'aucune information. Il faut donc utiliser une hypothèse de distribution intra-maille (uniforme, densité décroissante à partir du centre, etc.) pour procéder à cette estimation qui sera d'autant plus précise que l'on prend en compte des paramètres tels que la forme de la maille territoriale et plus précisément son allongement. La solution la plus fréquente consiste à utiliser comme référence une distribution uniforme de population dans un cercle de surface égale à la taille des mailles territoriales mais de nombreuses autres solutions ont été proposées dans la littérature d'analyse spatiale. L'une des plus astucieuses consiste à émettre l'hypothèse fractale d'une reproduction des inégalités de reproduction aux différentes échelles, c'est-à-dire à utiliser les paramètres de la distribution des distances moyennes inter-mailles en fonction de la surface totale de l'espace étudié pour estimer celle des distances intra-mailles. Mais en tout état de cause cette incertitude sur l'estimation des distances intra-maille a généralement une influence limitée sur le calcul de la distance moyenne entre les habitants du système puisque les couples d'habitants localisés à l'intérieur d'une même maille territoriale représentent dans la plupart des cas une très faible proportion de l'ensemble des paires d'habitants si les mailles sont nombreuses et de population équivalente (rappelons que cette fréquence est égale à l'indice d'homogénéité territoriale IX,M vu au chapitre précédent).
Au total, la formule générale d'estimation la plus simple et la plus fréquemment utilisée pour calculer les distances moyennes entre les habitants d'une population est la suivante :
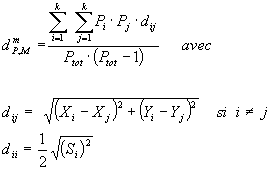
Quant à l'erreur d'estimation associée à cette
mesure, elle est plus difficile à mesurer dans l'absolu car elle
implique des hypothèses sur la forme de la distribution des habitants
à l'intérieur des mailles territroiales. On peut cependant
prendre comme ordre de grandeur de cette incertitude une mesure fondée
sur la variance de la surface moyenne des unités territoriales pondérées
par leur population que nous ne détaillerons pas ici.
Dans le cas de la population française en 1990, l'utilisation
d'un maillage territorial relativement fin, celui des 341 zones d'emploi
permet d'estimer la distance euclidienne moyenne entre deux habitants à
395 kilomètres environ. Cette valeur signifie que si l'on tirait
au hasard un grand nombre de paire d'individus et que l'on effectuait la
moyenne des distances euclidiennes entre les localisations de ces paires
d'individus on obtiendrait une valeur moyenne proche de celle de l'indicateur
proposée. Cette moyenne est évidemment un résumé
imparfait de la distribution de l'ensemble des distances entre les paires
habitants et nous verrons au chapitre suivant que d'autres résumés
peuvent en être proposés, mais elle suffira dans l'immédiat
à notre démonstration.
1.3.2 Calcul de la distance moyenne entre deux positions quelconques et mesure globale de la concentration spatiale
Ayant établi la distance moyenne entre deux habitants quelconques (situation observée), on peut maintenant se demander si elle révèle ou non une tendance à la concentration spatiale en proposant une ou plusieurs situations théoriques de distribution des habitants à l'intérieur du territoire français. On se limitera ici à deux approches très simples.L'hypothèse d'une distribution uniforme de la population française (densité égale en tout point de l'espace) implique que la quantité de population est rigoureusement proportionnelle à la superficie des mailles territoriales. Il est donc facile d'obtenir la distance théorique correspondante en remplaçant les populations par les surfaces des mailles territoriales dans le calcul de la distance moyenne. On obtient alors une estimation de la distance moyenne entre deux points quelconques du territoire français dmS,M qui est rigoureusement homologue à la mesure précédente de distance moyenne entre deux habitants du territoire français dmS,M . Il ne reste plus qu'à effectuer le rapport de ces deux distances pour obtenir une mesure de concentration spatiale exprimant les différences entre la situation observée et la situation théorique
I = dmS,M /dmP,M
La valeur de cet indice vaudra 1 si la concentration spatiale est nulle, il sera supérieur à 1 si les habitants sont plus proches en moyenne que deux points du territoire tirés au hasard et il sera inférieur à 1 si deux habitants sont en moyenne plus éloignés que deux points du territoire tirés au hasard.
L'hypothèse d'une distribution aléatoire de la population française complique quelque peu l'estimation de l'erreur de mesure de l'indice (qui va dépendre de la variance spatiale des densités) mais elle aboutit à une mesure équivalente dans la mesure où la distance moyenne entre deux points localisés au hasard à l'intérieur d'un espace à une limite qui tend vers la distance moyenne entre deux points quelconque lorsque le nombre de points est élevé et l'espace étudié de grande dimension (la situation serait évidemment très différente si l'on avait pris comme référence la distance moyenne au plus proche voisin et non pas la distance entre deux habitants quelconques).
Appliqué au cas de la France, on constate que la distance euclidienne moyenne entre deux points quelconque du territoire est également approximativement égale à 395 km de sorte que, compte tenu des erreurs de mesure on doit conclure à l'absence de concentration spatiale de la population française à l'intérieur de son territoire pour le critère de la distance euclidienne moyenne.
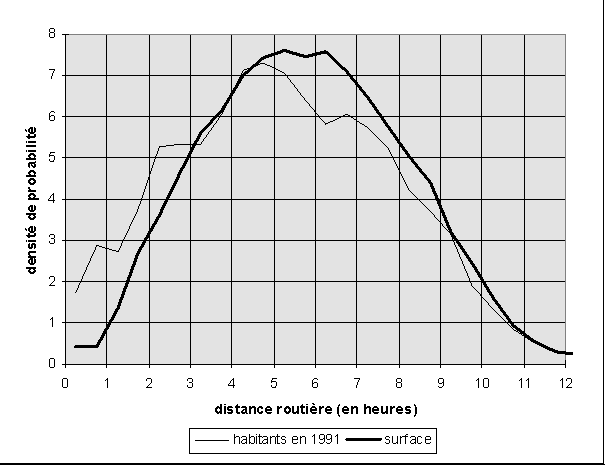
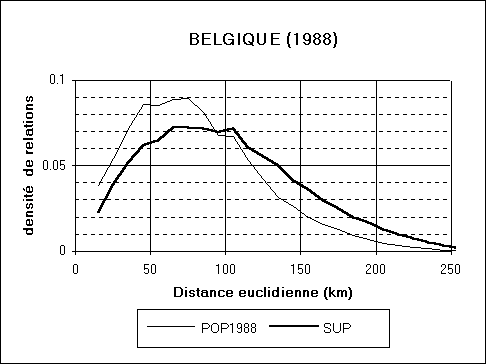
Ce résultat peut sembler paradoxal, mais il s'explique très simplement si l'on examine la distribution de l'ensemble des distances entre deux habitants ou entre deux points quelconques du territoire.
La comparaison des deux courbes de distribution des densités
de probabilité des distances montre une surreprésentation
des distances courtes entre les habitants (effet de l'accumulation
de la population dans les grandes métropoles) mais également
une surreprésentation des longues distances (effet du rejet à
la périphérie du territoire des zones de concentration du
peuplement autres que Paris). Le peuplement du territoire français
est donc concentré à l'échelle locale et dispersé
à l'échelle globale et il est donc parfaitement logique que
la distance moyenne qui prend en compte l'ensemble des distances aboutissent
à une valeur de concentration voisine de celle de la distribution
uniforme ou de toute autre distribution aléatoire !
1.3.3 Intérêt et limites d'une mesure globale de concentration spatiale
Un intérêt évident de l'indice proposé est d'être robuste par rapport au choix du maillage servant à calculer les distances moyennes entre deux habitants ou deux points quelconque de l'espace étudié. Cette robustesse étant d'autant plus forte que les biais qui peuvent être introduits dans l'estimation de la distance moyenne entre les habitants et la surface des mailles territoriales vont s'effectuer dans le même sens et que le rapport des deux a de forte chance de les corriger en grande partie.Son défaut, non moins évident est d'être peu discriminant par rapport à différentes distributions théoriques de répartition. En effet, la plupart des distributions aléatoires (uniforme, poissonienne, binomiale négatives) aboutissent à des valeurs identiques de l'indice dans la mesure où leur moyenne ne dépend que de la densité générale de la population sur l'ensemble du territoire et où l'on ne s'intéresse pas à la dispersion des distances par rapport à la valeur moyenne. Il est toutefois évident que ce défaut pourrait être corrigé si l'on introduisait d'autres paramètres relatifs aux moments centrés d'ordre deux, trois ou quatre de la distribution des distances moyennes entre les habitants ou les points de la superficie. Ces paramètres distingueraient alors plus clairement les distributions de type uniforme, aléatoire ou binomiale négative.
Toutefois, même en se limitant aux moments centrés d'ordre 1 (distance moyenne), l'indicateur de concentration globale peut se révéler utile lorsque l'on examine l'évolution du niveau de concentration spatiale à différentes dates pour une même métrique ou à une même date pour différentes métriques ou pour différents territoires à une même date avec la même métrique, etc.
Ainsi, si l'on substitue aux distances euclidiennes une estimation de la distance routière entre les zones d'emploi, on constate que le temps routier moyen permettant de mettre en relation deux habitants est signficativement plus faible (5h15 mn) que le temps routier moyen permettant de relier deux points quelconques du territoire (5h45mn). L'indice de concentration spatiale est donc significativement différent de 1, ce qui signifie que le réseau routier tend à rapporcher davantage les habitants que les différents points du territoire dans leur ensemble. Ce résultat s'explique par le fait que le réseau routier rapide relie de façon prioritaire les zones les plus densément peuplées du territoire et contribue de ce fait à accroître la concentration du peuplement, indépendamment de toute modification de la position des habitants. C'est en fait une expression de ce que l'on appelle la contraction espace-temps.
1.3.4 Exemple d'application des mesures de concentration spatiale : la comparaison de la répartition du peuplement dans trois pays.
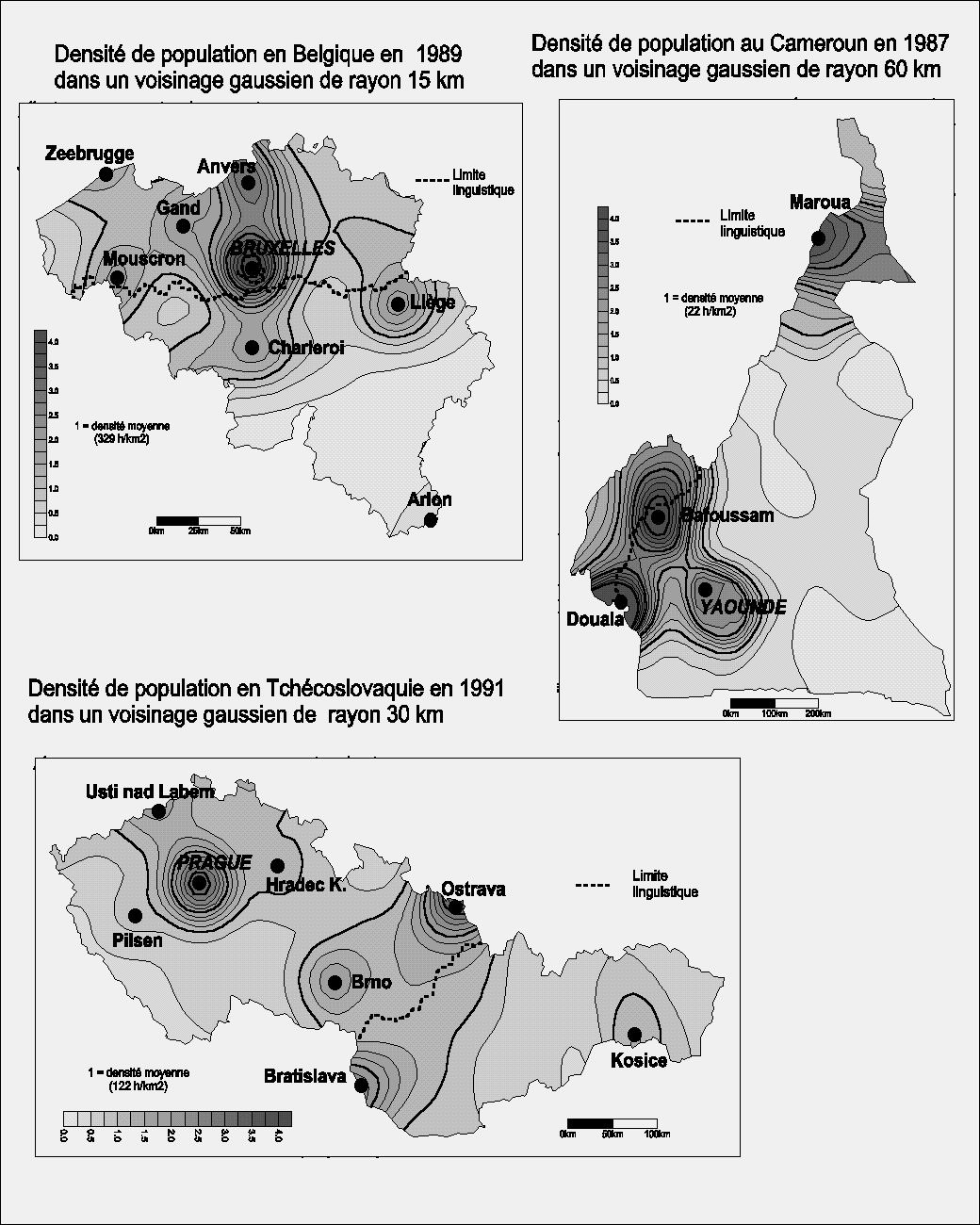
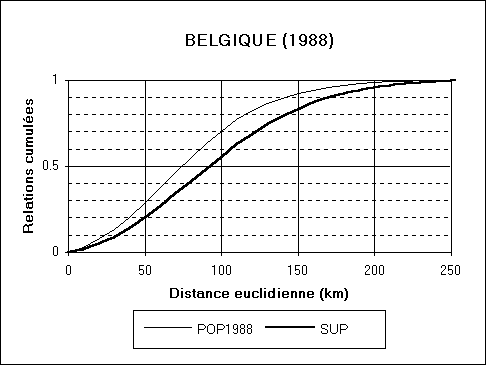
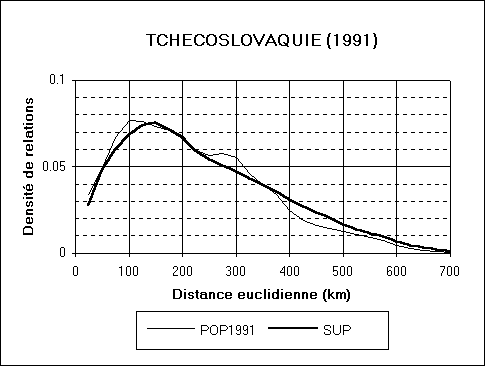
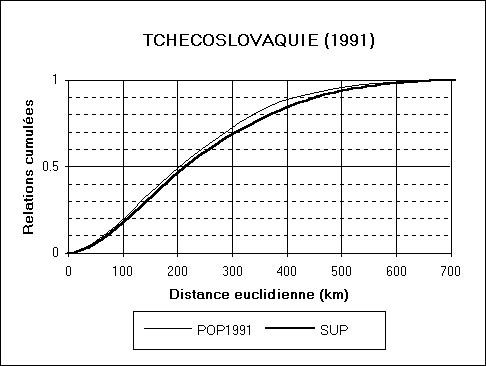
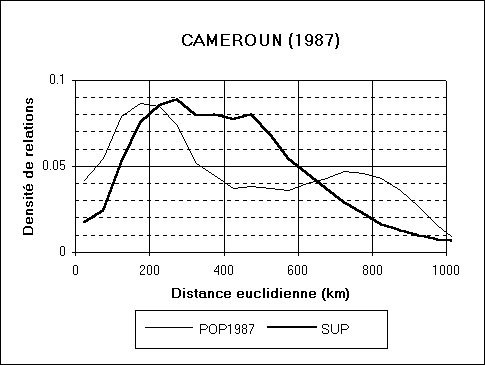
On se propose de comparer de la répartition de la populations
à l'intérieur de différents Etats de population voisine
mais de superficies différentes (Belgique, Tchécoslovaquie,
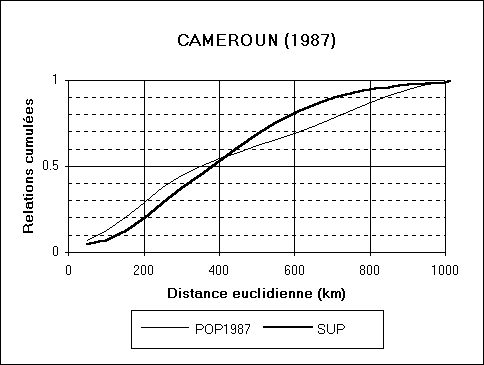
Cameroun). Pour ce faire, on commence par établir pour chaque pays
la distribution de fréquence des distances entre deux habitants
ou deux points quelconques du territoires et on la complète par
une distribution des courbes de fréquences cumulées (probabilité
que deux habitants ou deux points du territoire soient situés à
une distance supérieure ou égale à un certain seuil).
 |
 |
 |
 |
 |
 |
 |
| BELGIQUE | TCHECOSLOVAQUIE | CAMEROUN | ||||
| Superficie |
|
|
|
|
|
|
| * distance moyenne |
98 km
|
79 km
|
241 km
|
224 km
|
418 km
|
404 km
|
| * fréquences cumulées | ||||||
| d(25%) |
58 km
|
47 km
|
127 km
|
117 km
|
232 km
|
180 km
|
| d(50%) : distance médiane |
91 km
|
72 km
|
214 km
|
202 km
|
385 km
|
342 km
|
| d(75%) |
130 km
|
105 km
|
336 km
|
310 km
|
545 km
|
673 km
|
| * fréquences moyennes | ||||||
| mode principal |
85 km
|
75 km
|
150 km
|
100 km
|
350 km
|
200 km
|
| mode secondaire |
|
-
|
|
280 km
|
|
700 km
|