Cours  Exercices  Bibliographie  Menu précédent

Cours

Objectifs
1- Apprendre à éviter les confusions entre corrélation, association spatiale et causalité. Déjouer un certains nombres de pièges classiques dans l'interprétation des associations spatiales de variables.
2- Proposer un plan-type d'analyse pour les documents (cartes, graphiques) qui mettent en relation deux caractères décrivant les même lieux.
3- Apprendre à interpréter les résultats d'une analyse multivariée sans trop d'erreur (même si on ne connaît pas parfaitement les bases statistiques et mathématiques de ces méthodes ...).
 

A) QUELQUES  PIEGES CLASSIQUES

Comme il n'est pas question de dispenser un cours de statistique ou d'analyse spatiale à des étudiants se présentant au concours d'agrégation qui n'auraient pas acquis ces bases indispensables dans leur cursus antérieur, on va partir directement de l'inventaire des erreurs les plus souvent commises face à des documents. Considérons à titre d'exemple les résultats obtenus par 25 villes françaises pour le concours des "Dicos d'or" organisé par Bernard Pivot sur France 3 en 1993.
 

• La variable "nombre de fautes" (Y) est la somme des erreurs commises par les meilleurs candidats de chacune des séries ("professionnels", "adultes", "jeunes", ...) et elle a servi à établir un classement des villes lors du concours 1993 qui fut remporté par Toulouse avec 7 fautes seulement (25e rang pour le nombre de fautes ... donc 1er rang pour le niveau d'orthographe).
• La variable "population de l'agglomération en 1990" (X) a été introduite par nos soins afin de tester l'hypothèse d'une relation entre la taille des villes et leurs résultats au concours des Dicos d'Or. On remarquera qu'il existe un petit décalage chronologique entre les deux indicateurs (1993 et 1990) mais celui-ci n'est pas trop gênant dans la mesure où la population des villes est une donnée relativement stable. Il n'en va toutefois pas de même pour les résultats au concours des Dicos d'or et il aurait sans doute été utile d'effectuer la moyenne des résultats sur plusieurs années si l'on avait voulu procéder à une véritable étude scientifique. Mais la liste des villes qui participent au concours se modifie chaque année et le but de cet exemple est avant tout pédagogique, donc on s'en tiendra à l'information disponible.

Figure 1 : Relation entre taille des villes et nombre de fautes d'orthographe

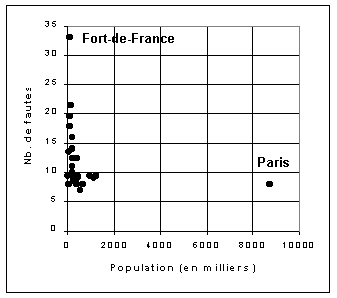
N.B. La relation statistique est faible. le coefficient de corrélation linéaire de Pearson affiche une valeur de -0.22 qui n'est pas significative au seuil de 5%

A.1) Premier piège : le problème des valeurs exceptionnelles

La figure 1 illustre un premier problème assez fréquent en géographie qui est celui des valeurs exceptionnelles. L'analyse d'une relation entre deux caractères X et Y est en effet complètement faussée lorsque certains individus ont des valeurs extrêmes sur l'un ou l'autre des indicateurs. Les coefficients de corrélation ne peuvent pas être interprétés de façon valable puisque la présence (ou l'absence) de relation significative est totalement déterminée par ces individus exceptionnels.

Dans l'exemple proposé, il faut donc noter le fait que Paris (pour la population) et Fort-de-France (pour le nombre de fautes d'orthographe) c onstituent des exceptions remarquables par rapport à l'ensemble des autres villes. On peut expliquer ces exceptions, mais, à ce stade, on ne peut rien dire de plus sur la présence ou l'absence d'une relation entre les deux caractères X et Y.

La démarche logique consiste, une fois que l'on a décrit ces exceptions, à reprendre l'analyse en les retirant et en justifiant ce retrait. Ce retrait a toutefois tendance à affaiblir la démonstration puisqu'il constitue une démarche ad hoc qui est toujours criticable.

Figure 2 : Relation entre taille des villes et nombre de fautes d'orthographe (sans Paris et Fort de France).

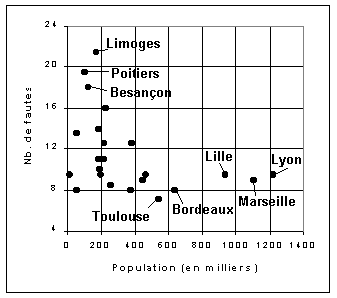
N.B. La relation statistique est  plus forte. Le coefficient de corrélation linéaire de Pearson affiche une valeur de -0.40 qui n'est pas tout à fait significative au seuil de 5% mais l'est au seuil de 10%

A la lecture du graphique, l'oeil perçoit assez nettement l'existence d'une relation négative entre le nombre de fautes d'orthographe et la taille des villes, mais l' indicateur statistique le plus fréquent (coefficient de corrélation linéaire)  ne confirme pas parfaitement cette hypothèse. Il y a en effet 5 a 10% de chances que la relation qui a été détectée soit simplement l'effet du hasard. A ce stade, on ne peut donc pas affirmer avec certitude qu'il existe une relation entre les deux variables.
 

A.2) Deuxième piège : relations linéaires et relations non-linéaires

En fait, le caractère décevant des résultats tient au fait que le modèle qui a été utilisé implicitement pour tester la relation n'était pas adapté. Il est bien visible sur le Figure 2 que la relation entre la taille des villes et le nombre de fautes d'orthographe n'est pas linéaire : le nombre de fautes décroît rapidement pour les villes de 100 à 300 000 habitants puis semble se stabiliser pour les villes ayant une population supérieure à 500 000 habitants. Or, le coefficient de corrélation qui a été employé suppose l'existence d'une relation linéaire de type Y=aX+b dans laquelle b serait le nombre maximal de fautes (pour une ville de taille minimale) et a la décroissance du nombre de fautes chaque fois que la population de la ville augmente d'une certaine tranche de population. Ce modèle apparaît d'autant plus inadapté qu'il impliquerait, s'il était vrai, que le nombre de fautes devient nul voire négatif au delà d'une certaine taille des agglomérations !

Pour résoudre cette difficulté, on peut utiliser des modèles statistiques plus complexes (exponentiel, puissance), mais il est également possible de recourrir à une solution plus simple qui consiste à transformer les caractères quantitatifs étudiés X et Y en variables ordinales (rang pour la population, rang pour le nombre de fautes d'orthographe). Cette transformation est ici d'autant plus logique que le but de l'épreuve des  Dicos d'or était précisément d'établir un classement des villes.
 

Figure 3 : Relation entre les rangs pour la taille des villes et les rangs pour le nombre de fautes d'orthographe

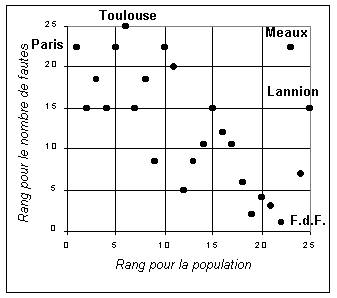
N.B. La relation statistique est  encore plus  forte. Le coefficient de corrélation de rang de Spearman affiche une valeur de -0.49 qui est significative au seuil de 5%. On remarquera que Paris et Fort-de France ont été réintroduits dans l'analyse et ne constituent plus des valeurs exceptionnelles. Les deux villes qui constituent les exceptions les plus remarquables sont désormais Lannion et Meaux : si on les retirait, le coefficient de corrélation de rang passerait à -0.76 et serait significatif au seuil de 1%.

On remarquera que le passage au variables ordinales a permis de réintroduire Paris et Fort-de-France qui ne constituent plus désormais des valeurs exceptionnelles. On évite ainsi la critique consistant à produire un modèle ad hoc (Cf. A.1) tout en ayant produit un modèle qui est désormais significatif sur le plan statistique (le seuil d'erreur de 5% est celui qui est habituellement retenu en sciences humaines). On pourrait retirer Lannion et Meaux de l'analyse pour obtenir une relation meilleure, mais cela n'apparaît pas absolument nécessaire et il vaut mieux considérer que les écarts au modèle de ces deux villes constituent des résidus intéressants et interprétables du modèle principal.
 

A.3) Troisième piège : corrélation, causalité et association spatiale

La difficulté principale va consister à commenter et à interpréter les résultats obtenus, c'est-à-dire à proposer une explication de la relation qui a été mise en évidence sur le plan statistique. Cette étape cruciale est celle où l'on observe les erreurs les plus graves en raison de la confusion souvent faite entre les notions de corrélation, causalité et association spatiale.
 

• La corrélation renvoie à  un ensemble d'outils statistiques permettant de détecter, décrire, tester la présence de relations de dépendance significatives entre des caractères qualitatifs, quantitatifs, ordinaux. Au sens strict, le terme de corrélation a trait à la mesure de relations entre deux caractères quantitatifs (e.g. coefficient de corrélation linéaire de Pearson) ou ordinaux (e.g. coefficient de corrélation de Spearman) mais on peut étendre son usage à la mesure de la relation entre deux caractères qualitatifs (e.g. test du chi-2) ou entre un caractère qualitatif et un caractère quantitatif (e.g. analyse de la variance, test de Student). Le terme générique permettant de décrire l'ensemble de ces relations est celui de dépendance. On dit qu'une variable Y dépend d'une variable X si la connaissance des modalités de X permet de prédire (dans une certaine mesure, avec une certaine imprécision) les modalités de Y. Or, il faut insister sur ce point, la prévision n'implique pas nécessairement l'explication. Certains modèles "stupides" permettent d'excellentes prévisions (e.g. modèles markoviens utilisés en climatologie ou en spéculation boursière) en se fondant uniquement sur la prise en compte du maximum de situations passées analogues à la situation présente.

 

 

=> En d'autres termes, la corrélation observée entre les deux variables de notre exemple signifie que la connaissance de la population d'une ville  en 1990 permet de prédire (dans une certaine mesure, avec une certaine marge d'erreur) les résultats qu'elle aurait pu obtenir au concours d'orthographe des Dicos d'or en 1993. Si Rennes avait participé à l'épreuve de 1993, sa population et le rang correspondant l'auraient probablement situé aux alentours de la 10e place avec un total d'une quinzaine de fautes. Il est de ce point de vue intéressant de remarquer que la non-participation de Rennes explique sans doute pour une large part l'excellent résultat de Lannion
 

• La causalité est une interprétation explicative de la corrélation qui repose sur des hypothèses et implique des vérifications complémentaires de ces dernières. Affirmer que "plus les villes sont grandes, meilleurs sont leurs résultats en orthographe"  est une affirmation qui ne pose pas de problèmes particuliers puisqu'elle relève du simple constat descriptif. En revanche, affirmer que "c'est parce qu'elles sont plus grandes que certaines villes ont obtenu de meilleurs résultats en orthographe" est une explication causale, une interprétation qui doit être précisé et justifiée. Il existe en effet de très nombreuses manières d'interpréter une corrélation à l'aide de chaînes causales comme le montre la figure 4 et l'hypothèse d'une causalité dircte (X est cause de Y ou Y est cause de X) est un cas particulier des explications potentielles de la corrélation observée entre deux caractères X et Y. Certaines explications proposées sont volontairement fantaisistes, tandis que d'autres apparaissent davantage plausibles. Mais en tout état de cause, il n'est pas possible de trancher aisément entre elles si on ne mobilise pas des informations plus précises et à d'autres niveaux d'analyse (e.g. enquête sur les participants au concours dans les différentes villes).

• L'association spatiale constitue un simple constat descriptif, analogue à la corrélation, mais qui ajoute un certain nombre d'éléments supplémentaires dans l'interprétation. Le fait qu'unecorrélation soit établie entre des lieux et non pas des individus statistiques quelconque permet en effet d'introduire un certain nombre d'éléments complémentaire dans l'analyse des résultats, le premier étant évidemment la cartographie des deux variables étudiées ainsi que celle des résidus de régression. La prise en compte de la dimension spatiale du phénomène de corrélation est à la fois une source considérable d'enrichissement de l'analyse, mais aussi un danger redoutable puisqu'elle peut conduire à des erreurs très graves d'interprétation si l'on n'est pas très vigilant sur le niveau d'analyse auquel les relations ont été établies.

 

 

=> Un exemple d'enrichissement de l'analyse est fourni par l'analyse spatiale des résidus de la relation entre niveau d'orthographe et taille des villes. On remarque en effet deux très forts résidus positifs (Lannion et Meaux) qui correspondent à des villes où le niveau d'orthographe est beaucoup plus élevé que ce que laisserait prévoir la taille des villes. Or, un géographe ne manquera pas de remarquer que Meaux est situé à proximité immédiate de Paris (et a pu attirer de nombreux candidats de la banlieue est) tandis que Lannion est situé à proximité de Rennes et de Brest qui n'ont pas participé au concours, ce qui faisait de Lannion le seul centre de concours en Bretagne (Nantes mis à part). On peut donc supposer que la taille de ces villes ne reflète pas le bassin de recrutement des candidats qui les ont choisi comme points de ralliement et on peut supposer que ce décalage explique les scores exceptionnels qu'elles ont obtenu.
=> Un exemple d'erreur d'interprétation grave consisterait à affirmer que "Les habitants des grandes villes ont un niveau d'orthographe supérieur aux habitants des petites villes". Il s'agit en effet d'une erreur écologique qui consiste à transposer au niveau des individus une conclusion tirée au niveau des agrégats sociaux constitués par les lieux. Rien ne permet en effet de tirer une telle conclusion dans les données fournies et il est beaucoup plus raisonnable de supposer que, si les bons candidats sont répartis au hasard dans la population française, les grandes villes qui attirent plus de candidats ont de meilleures chances d'obtenir de bons résultats (puisque le score d'une ville est la somme des fautes de ses meilleurs candidats et non pas la moyenne de tous les candidats présents)

B) LA MISE EN RELATION DE DEUX CARACTERES DANS LE CADRE D'UN COMMENTAIRE DE DOCUMENTS

Après avoir passé en revue quelques erreurs très fréquentes (et incité ce faisant les candidats à l'agrégation à vérifier la solidité de leurs bases en statistiques ...) on va proposer un schéma plus générale d'analyse de la relation entre deux caractères dans le contexte d'une épreuve de commentaires de documents.

Comme les candidats ne disposeront pas de moyens de calcul au moment de l'épreuve, il n'auront vraisemblablement pas à effectuer des traitements statistiques mais plutôt à interpréter des résultats qui leurs seront fournis sous la forme de tableaux, de cartes ou de graphiques.Tout au plus auront-ils peut-être à réaliser ou compléter  un graphique (e.g. tracer une droite de régression) ou une carte (e.g. cartographier les résidus) mais ils seront jugés avant tout sur l'interprétation correcte des documents proposés.

Le plan-type que nous proposons pour une épreuve de ce type ne constitue pas un moule rigide mais doit être adapté aux documents proposés. Il permet toutefois de passer en revue un certain nombre de réflexes que le candidat doit acquérir lorsqu'il est confronté à la mise en relation de deux caractères. L'application pratique sera faite sur les documents de l'exercice n°5.

B.1) Analyser la relation proposée

Après avoir rappelé brièvement les propriétés de la matrice d'information géographique qui sert de base à l'étude ( unités spatiales, variables, période, contexte spatial et territoriale ... Cf. module n°2), il faut préciser quelles sont les deux variables mises en relation et, indiquer celle qui joue le rôle de variable dépendante (Y : variable à expliquer) et celle qui joue le rôle de variable indépendante (X : explicative).

Si le document proposé est un graphique, il faut se souvenir que, de façon conventionnelle, la variable indépendante correspond à l'axe des abcisses  (X)  et la variable dépendante à l'axe des ordonnées (Y). Ainsi, dans l'exemple des précipitations en Californie, on tente d'expliquer les précipitations (Y) par la latitude (X) des stations et le graphique qui exprime cette relation utilise les axes en conséquence (Cf. document n°4 de l'exercice 5).

Même si la relation à étudier est clairement indiquée dans les documents, il n'est pas inutile de justifier le choix de cette relation en invoquant soit des arguments statistiques (présence d'une corrélation forte et significative : Cf. document n°2 de l'exercice n°5), soit des arguments thématiques (pourquoi est-il logique de penser que Y dépend de X ?). On doit être trés attentif à bien distinguer les deux types d'arguments puisque les premiers relèvent d'une démarche prédictive (la plus forte corrélation fournit la meilleure prévision) tandis que les seconds relèvent d'une démarche explicative (les connaissances acquises par le candidat dans son cursus de géographie lui fournissent différentes hypothèses explicatives).

Il faut également être très attentif au contexte spatial et territorial qui sert de cadre à l'analyse. Dans l'exemple de l'exercice n°5, la variable qui semble rendre le mieux compte des précipitations est la latitude, mais les conclusions pourraient être différentes si on avait travaillé sur un espace plus réduit (rôle majeur de l'altitude) ou plus vaste...

Il faut également être critique vis à vis des documents proposés, le jury d'agrégation étant tout à fait capable de fournir des documents biaisés ou un modèle de mauvaise qualité. Ainsi, dans l'exemple des précipitations, onpeut s'étonner que la variable "situation d'abri" ne figure pas dans la matrice de corrélation. Le fait qu'il s'agisse d'une variable qualitative n'explique pas tout. de fait, si on avait testé son pouvoir explicatif, on aurait pu voir qu'il était supérieur à celui de toutes les autres variables, y compris la latitude.

Enfin, il faut dans la mesure du possible essayer de se détacher de l'outil statistique pour produire des interprétations précises mais concrètes, simples et intelligibles par un public non statisticien (rappelons que les agrégés sont de futurs enseignants du secondaire).  Ainsi, plutôt que de dire que "les précipitations (Y) sont une fonction linéaire  Y=92.6*X-2923 de la latitude(X) avec un coefficient de détermination de 0.33 ...." on pourra dire plus simplement que "Les précipitations augmentent en moyenne d'environ 100 mm chaque fois que la latitude augmente d'un degré, du sud au nord de la Californie. Ce modèle permet de rendre compte d'environ un tiers des différences de précipitaton observées entre les stations californiennes ..."

B.2) Analyser les résidus

Une fois que l'on a établi la relation principale, qu'on a tenté de la décrire et de l'expliquer, il faut s'interroger sur les résidus du modèle, c'est-à-dire à la part des variations de Y qui ne peuvent pas être imputées à X. Rappelons pour mémoire que le pouvoir explicatif d'un modèle de régression est égal au carré du coefficient de corrélation entre X et Y (aussi appelé coefficient de détermination) et que les résidus correspondent à tout ce qui n'est pas expliqué par le modèle.

Dans l'exemple des précipitations en Californie, le coefficient de détermination des précipitations par l'altitude n'est que de 33%, ce qui signifie que "près des 2/3 des différences de précipitation observées entre les stations de Californie doivent être imputées à d'autres facteurs explicatifs que la latitude".

Selon les documents fournis, l'analyse des résidus et la recherche d'autres facteurs explicatifs peut être menée soit à l'aide de graphiques  (Cf. document n°4 de l'exercice n°5), soit à l'aide de tableaux (e.g. liste des unités ayant les plus forts résidus positifs et négatifs), soit enfin à l'aide de cartes (Cf. document n°5 de l'exercice n°5).

L'analyse des résidus doit être très précise et éviter les contresens. Ainsi, un résidu nul ne signifie pas que "les précipitations sont nulles" dans l'exemple Californien, mais simplement que "la valeur observée est conforme à ce que l'on peut prévoir compte tenu de la latitude de la station". De la même manière, les résidus négatifs ne constituent pas des "déficits de précipitation" mais des "précipitations plus faibles que prévues compte tenu de la latitude" et les résidus positifs ne correspondent pas à des "excédents de précipitations" mais à des "précipitations plus fortes que prévues compte tenu de la latitude".

L'analyse des résidus a généralement pour objectif de découvrir un effet secondaire masqué par un effet principal. Ainsi, le candidat qui n'aurait pas repéré l'effet des situations d'abri sur les précipitations sur la carte initiale des précipitations ne peut pas la manquer lorsqu'il considère attentivement les documents qui lui sont fournis (comparaison de la carte des résidus et de la carte des stations abritées, analyse des points situés au dessus ou au dessous de la droite de régression). Il doit logiquement conclure que "à latitude égale, les précipitations varient fortement en fonction de l'exposition des stations au vent dominant" et effectuer à ce sujet d'utiles rappels sur la circulation d'ouest aux latitudes moyennes, les effets de Foehn, etc.

On ne doit toutefois jamais perdre de vue que la présence de résidus peut également être le résultat d'une mauvaise spécification du modèle ou d'un mauvais choix de la variable explicative initiale (X). Ainsi, dans l'exemple des Dicos d'or analysé précédemment, un ajustement linéaire effectué sur le nuage de point  initial (Cf. document 1) aurait fait apparaître de très forts résidus positifs pour Paris et Fort-de-France et on aurait conclu à tord que "ces villes ont une orthographe déplorable compte tenu de leur taille". La relation étant non-linéaire, l'ajustement utilisé conduisait à des résultats aberrants qu'il ne fallait surtout pas interpréter. Dans le cas de la relation correcte entre les rangs (Cf. Document 3) il est par contre tout à fait légitime d'interpréter les résidus et nous avons vu qu'il était possible de donner une explication plausible des écarts observés pour Lannion et Meaux en tenant compte de leur situation géographique (Cf. un exemple d'enrichissement de l'analyse).

B.3) Réévaluer et enrichir le modèle initial

En fonction des résultats de l'analyse détaillée du modèle et de ses résidus, on peut proposer différents types d'améliorations. On indiquera juste ici quelques grandes familles d'enrichissement :
 

• Ajout de nouvelles variables. On peut remplacer le modèle initial Y=aX+b par un modèle plus complexe introduisant de nouveaux facteurs (Z,W) déduits de l'analyse des résidus et tester un modèle du type Y=aX+bW+cZ+d, en vérifiant évidemment que toutes les variables introduites sont significatives et non redondantes. Il peut arriver que, ce faisant, on soit amené à supprimer la variable explicative initiale (X) si on se rend compte que son effet explicatif est finalement négligeable quand on tient compte de celui des nouvelles variables Z et W.
• Segmentation spatiale du modèle. Si l'analyse du nuage de point ou des résidus révèle l'existence de discontinuités nettes (groupes de lieux obéissant à des relations différentes) on peut être amené à segmenter le modèle c'est-à-dire à proposer des ajustements différents pour des sous-ensembles de lieux. On aura ainsi un modèle Y=a1X+b1 pour certains lieux et Y=a2X+b2 pour d'autres lieux, la segmentation étant souvent la clé d'une régionalisation. Ainsi,on pourra observer que  la relation entre température et altitude n'obéira pas à la même loi sur les adrets et les ubacs d'une vallée.
• Amélioration de la variable explicative X. Si l'on découvre par exemple que les résidus d'un modèle de prédiction des flux en fonction de la distance euclidienne sont systématiquement sous-estimés ou sur-estimés lorsque les infrastructures de transport sont respectivement de très bonne qualité ou de très mauvaise qualité, il semble logique de reconstruire le modèle en remplaçant la distance à vol d'oiseau par une mesure plus réaliste de temps ou de coût généralisé de transport

Même si les conditions matérielles de l'épreuve de commentaire de documents ne permettent pas de tester ces différentes améliorations, il est essentiel de les suggérer en conclusion du commentaire afin de montrer que l'on est capable de dépasser le stade de l'analyse passive de l'information fournie par le jury. Celui-ci ne sera certainement pas vexé, bien au contraire, de découvrir des candidats potentiellement capables de reprendre et d'améliorer l'information contenue dans les documents fournis. Cette démarche active est sans doute  une différence fondamentale entre ce que l'on attend des candidats à  la nouvelle épreuve d'agrégation et une simple mise en ordre de connaissance de type du "dossier documentaire" réalisé par les élèves de terminale pour l'épreuve d'histoire-géographie au baccalauréat.

CONCLUSION

Une très bonne maîtrise des notions de corrélation, causalité et association spatiale peut et doit être exigé des candidats à l'agrégation, faute de quoi ils risquent de proférer des absurdités devant leurs futurs élèves qui ne pourraient que nuire à l'image de notre discipline. Les candidats qui n'auraient pas approfondi ces notions pourraient de plus être la dupe d'idéologues sans scrupules qui n'hésitent pas à utiliser des raisonnement pseudo-scientifique où la géographie sert souvent d'alibi (Cf. Exercice n°6).
 
 

A RETENIR :
 

Il ne faut pas confondre les notions de corrélation, causalité et association spatiale.  Prédiction et explication sont deux choses différentes L'erreur écologique (confusion entre une corrélation établie au niveau des lieux et une corrélation établie au niveau des individus) est une confusion  très grave mais malheureusement très fréquente en géographie L'analyse des résidus d'une relation est tout aussi importante que l'étude de la relation proprement dite.  Les résidus ne sont interprétables que si la relation établie est correcte sur le plan statistique et sur le plan thématique.

Exercices

EXERCICE N°4
    L'erreur écologique
     sujet : Enquête sur l'alcoolisme dans la résidence universitaire de Trifouilly

EXERCICE N°5
    Mise en relation de deux caractères
     sujet : Les précipitations en Californie
 

EXERCICE N°6
    Un exemple de confusion volontaire entre corrélation & causalité
     sujet : Richesse, pauvreté et contraintes géographiques
 
 

Bibliographie

Pour réviser les notions de base sur la corrélation et la régression en géographie, on peut se reporter aux chapitres correspondants dans les ouvrages suivants :

• Béguin M., Pumain D., 1994, La représentation des données géographiques, Colin, coll. Cursus, Paris, 192 p.
• Chadule (groupe), 1997, Initiation aux pratiques statistiques en géographie, Paris : A. Colin - Masson, 1997.
• Chauvat G., Reau J.P., 1985, Statistiques descriptives : DEUG sciences éco et AES 1re année droit et sciences humaines (psychologie, sociologie, géographie, histoire), Paris : A. Colin
• Chemla G., 1995, Statistique appliquée à la géographie : représentations graphiques, sources et méthodes, Paris : Nathan
• Lahousse P., Piédanna V., 1999, L'outil statistique en géographie - Tome 2 : L'analyse bivariée, Paris : A. Colin
• Vigneron E., 1997, Géographie et statistique, Paris : Presses universitaires de France, Coll. QSJ

 

• Grasland C., 1994, "L'erreur écologique en géographie", Feuilles de Géographie n°1, vol. I-1994, 4 p.

• Grasland C., 1995, "Modélisation et commentaire de documents", Feuilles de géographie n°16, vol. IV-1995, 20 p.