Cours  Exercices  Bibliographie  Menu précédent

Cours

Objectifs

1- Apprendre à réaliser une classification fondée sur l'emploi d'outils simples, accessibles dans le cadre d'une épreuve écrite
2- Apprendre à interpréter les résultats de méthodes de classification plus complexes.
3- Apprendre à distinguer classification et régionalisation.
 

A) ORIGINE, DEFINITION ET OBJECTIFS DE L'ANALYSE TYPOLOGIQUE

1) Une brève histoire de la classification

a) Antiquité-Moyen-Age

Le problème de la classification est consubstantiel à la démarche de nombreuses sciences car une bonne classification permet non seulement de résumer des connaissances mais aussi de les enrichir en révélant des différences et des ressemblances invisibles jusque là. Aristote est l'un des plus grands classificateurs devant l'éternel.

b)  XVIIIe-XIXe

 En dehors des sciences humaines, la classification ou taxinomie s'est développée au départ en zoologie et en botanique avec les travaux de Linné ou de Buffon entre autres. Ce n'est que vers le milieu du XXe siècle qu'elle s'étend à des domaines autres que les sciences naturelles. Ces classifications sont essentiellement déductives, s'appuyant sur l'ajout progressif de critères qui forment un arbre. Elles consistent à fragmenter progressivement l'ensemble d'élément en fonctions de critères hiérarchisés.

ex. Classification des climats de Köppen

1) Bilan annuel de l'eau ( EXCEDENTAIRE/DEFICITAIRE/TRES DEFICITAIRE)
2) Période froide (ABSENTE/MODEREE/MARQUEE)
3) Période sèche (ABSENTE/ETE/HIVER)
4) Température en été (4 modalités en fonction du mois le plus chaud)

=> il y a théoriquement 3x3x3x4= 108 climats possible, certaines configuration étant toutefois exclues (bilan très déficitaire implique absence de période sèche).

c) le tournant des années 1940-1960

A partir des années 1950-1960, les ordinateurs se multiplient et les techniques de classification automatique deviennent accessible à un public plus large. On assiste alors à une montée en puissance des classifications inductives qui ne privilégient pas un groupe restreint de variable mais examinent les regroupements d'individus décrits par un très grand nombre de critères.

ex. Le réexamen de la classification des climats

La classification de Köppen s'appuyait sur une sélection de quatre variables climatiques réduites à un nombre limité de modalités. Les nouvelles techniques de classification permettent d'utiliser un beaucoup plus grand nombre de variables et de ne pas fixer a priori les classes de ces variables lorsqu'il s'agit de caractères continus (températures, précipitations). Les types de climats sont définis a posteriori par le regroupement des stations les plus proches sur l'ensemble des critères (L. Sanders et F. Durand-Dastès, 1984 ; F. Durand-Dastès, 1987).

d) l'explosion des années 1960-1980

Au cours des vingt années suivantes on assite à une multiplication des techniques et des algorithmes de classification et à leur diffusion dans l'ensemble du champ scientifique et également dans le champ industriel et économique (analyse des segments de marché, par exemple).

Il s'ensuit une relative confusion, jusqu'à ce que paraissent des programmes standard (classification ascendante hiérarchique) et des ouvrages de synthèse (Jambu, 1978 ; Chandon J.L., Pinson S., 1981).
 
 

2) Définition et paradoxe de la classification
 

Pour le philosophe Canguilhem (1972), l'analyse typologique est "une méthode d'analyse des données qui permet de grouper des objets, caractérisés par un ensemble d'attributs ou de variables, en classes non nécessairement disjointes deux à deux. Ces classes doivent être d'une part aussi peu nombreuses que possibles et d'autre part aussi homogènes que possibles" (cit‚ par Chandon J.L. et Pinson S., p. 4). L'analyse typologique doit donc réaliser un compromis entre deux contraintes antinomiques :

(a) restreindre le nombre de classes pour simplifier l'information initiale.
(b)  obtenir des groupes aussi homogènes que possible, ce qui tend à accroître le nombre de classes puisque la partition la plus homogène est celle qui fait de chaque élément une classe.

                                -                                               +
Simplification de -------------->   Nombre de <----------------    Homogénéité
l'information                                  Classes                                   des classes
 

3) Objectifs de la classification
 

Selon Chandon et Pinson (1981) la classification peut permettre de remplir six grands types d'objectifs :

a) réduction des données : en ramenant N individus à K classes, puis en limitant l'analyse a un représentant-type de chaque classe.

b) exploration des données : comme phase exploratoire avant toute autre méthode d'analyse des données, l'analyse typologique permet de répondre aux questions suivantes

•  mon échantillon est-il hétérogène ?
•  existe-t-il des individus marginaux ?
•  l'introduction de nouveaux éléments ou de nouvelles variables perturbe-t-elle la classification obtenue ?

On peut alors décider d'ajouter ou de retirer certains éléments et certaines variables pour obtenir un tableau de données plus cohérent.

c) classification des données : beaucoup de problèmes ont pour objectif l'obtention d'une classification respectant un certain nombre de contraintes (nombre de classes fixé a priori, contrainte de contiguité imposée aux éléments dans les problèmes de régionalisation, etc).

d) validation d'hypothèses : on peut tester si une classification a priori émerge bien lorsque l'on réalise une analyse typologique sans a priori sur les classes qui seront produites. Ainsi, si on pense a priori que la CSP influe sur les comportements d'achats de tel famille de produits, on réalisera une enquête sur un échantillon de personnes de différentes CSP pour voir si elles se regroupent dans les mˆmes classes pour les critŠres retenus.

e) prédiction fondée sur la nature des groupes : les classes définissent des ensembles d'éléments ayant le même comportement par rapport à un ensemble de variables. Lorsque l'on ignore le comportement d'un individu sur une variable, on peut essayer le prédire par son appartenance à telle ou telle classe. Ceci s'applique par exemple pour la détermination des risques en médecine : l'appartenance à  une classe sur-représentant le tabac, l'alcool, les graisses détermine a priori un risque supérieur d'exposition à certaines pathologies (Cancer, maladies cardio-vasculaire, etc). Ce genre d'analyse est toutefois possible également à l'aide des méthodes d'analyse factorielle  (ACP ou AFC).

f) génération d'hypothèses : l'apparition de groupes empiriques (induction) peut suggérer des hypothèses sur leur constitution qui seront ensuite validées (déduction).
 

4) Les grandes familles de classifications

Trois grandes familles de classification peuvent être définies en fonction de l'ordre de regroupement des individus.

a) classifications descendantes hiérarchiques

On part de l'ensemble des individus regroupés en une seule classe, puis on cherche la division optimale en deux classes. On examine ensuite laquelle de ces deux classes il faut partitionner pour obtenir un regroupement optimal en trois classes et ainsi de suite. La méthode est hiérarchique car elle n'autorise pas de retours en arrière : une fois que deux éléments sont séparés, ils ne peuvent plus être regroupés dans la même classe.

b) classifications ascendantes hiérarchiques

On part d'un nombre de classe égal au nombre d'individus et on regroupe les deux individus les plus proches pour obtenir N-1 classes. A l'étape suivante on regroupe soit les deux classes les plus proches, c'est à dire soit deux individus, soit un individu et la première classe de deux éléments. On procède ainsi jusqu'à ce que tous les éléments soient regroupés dans une seule classe. La méthode est hiérarchique là encore car deux individus regroupés ne peuvent plus être séparés au cours des itérations suivantes.

c) Classification autour de noyaux mobiles

Malgré de nombreuses variantes, ces techniques de classification ont pour point commun de partir d'une partition prédéfinie en K classes. A chaque étape, un individu passe d'une classe à une autre pour accroître l'homogénéité globale de la partition. L'algorithme s'arrête lorsque plus aucun déplacement ne peut améliorer la partition obtenue. Au cours du processus, des classes peuvent disparaître, si tous leurs éléments sont déplacés vers une autre. Ces méthodes ont l'inconvénient d'être sensibles à  la partition initiale qui peut entraîner la convergence vers un optimum local et non global. On procède généralement à plusieurs essais avec des partitions initiales différentes. Dans certains cas, on utilise également des classes d'appartenance floues.
 

B) METHODES ELEMENTAIRES DE CLASSIFICATION

Si l'on considère un ensemble de lieux (1..i...n) décrits par un ensemble de caractères (X1...Xk), on peut définir la classification comme une opération visant à constituer des sous-ensembles de lieux appelés classes (C1..Cz), définis de telle sorte que la ressemblance soit maximum entre les lieux appartenant à la même classe et minimum entre les lieux appartenant à des classes différentes.

B.1) Classifications fondées sur un critère unique (discrétisation)

Ceci paragraphe constitue juste un rappel pour signaler que les discrétisations qui sont à la base de nombreuses représentations cartographiques constituent bel et bien une opération de classification. Les différentes méthodes utilisées pour définir les classes (effectifs égaux, amplitudes égales, moyenne et écart-type, moyennes mobiles, méthode de Jenks) sont autant de solutions au problème de la classification lorsque les lieux sont décrits par un attribut unique. Le paradoxe central de la classification (différencier le mieux possible, avec le minimum de classes) s'applique évidemment parfaitement au cas des représentations cartographiques. On notera juste l'intérêt de deux méthodes souvent peu connues des étudiants mais qui sont particulièrement représentatives des discussions précédentes sur les objectifs de la classification.
 

• La méthode des moyennes mobiles est typiquement une méthode déductive utilisant une  classification descendante puisqu'elle consiste à scinder l'échantillon entier (N) en deux sous-ensembles (N1 et N2) en fonction de la valeur seuil constituée par la moyenne Xn. Puis à construire 4 classes en scindant chacun des échantillons N1 et N2 en fonction de leurs moyennes respectives Xn1 et Xn2. Et à poursuivre éventuellement l'opération pour passer à 8 classes ...
• La méthode de Jenks est au contraire une méthode inductive qui consiste à choisir les seuils qui maximisent la variance inter-classe et minimisent la variance intra-classe. Si la distribution comporte des discontinuités (zones de faible densité des valeurs) celles-ci seront nécessairement détectées par la méthode de Jenks qui constitue une variante  rigoureuse de la méthode bien connue des "seuils naturels".

Figure 1 : Densité de population des départements camerounais en 1976 (graphique ordinaire)

Commentaires : On repère bien l'existence de deux valeurs exceptionnelles (les départements correspondant aux villes de Douala et Yaoundé) et une rupture vers 90 h/km2, mais il est difficile d'analyser les variations de densité entre 0 et 100 h/km2.

Figure 2 : Densité de population des départements camerounais en 1976 (graphique logarithmique)

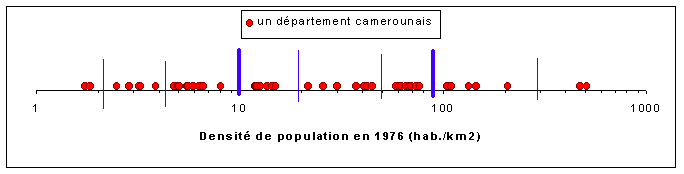Commentaires : l'utilisation d'une échelle logarithmique permet, dans le cas de la présente distribution, de beaucoup mieux repérer les zones de concentration et de dispersion des valeurs. On en déduit des ruptures majeures (vers 10 et 90 h/km2) et des ruptures secondaires (vers 2, 4, 20, 50 et 300 h/km2) qui pourront servir plus tard de base à la définition des limites de classes.

B.2) Combinaison de deux critères

Un cas très fréquent et très important est celui de l'établissement d'une classification fondée sur la combinaison de deux critères (X et Y).

Identifier une ou plusieurs problématiques latentes

Avant toutes choses, il faut se demander pourquoi ces deux critères ont été rapprochés et quel est l'intérêt de leur croisement en termes de problématique.

• Si les deux critères considérés sont le taux de natalité et le taux de mortalité, il est évident que la problématique sous-jacente est celle de la transition démographique et on ne devra pas perdre de vue que la position des points dans l'espace des deux variables permet de déduire un troisième indicateur qui est le taux d'accroissement naturel.
• Si au contraire le graphique croise une variable d'état (e.g. PNB par habitant en 1960) et une variable d'évolution (e.g. variation du PNB entre 1960 et 2000), la problématique devra être centrée sur les questions de convergence-divergence des lieux.

Figure 3 : Population et PNB de 56  états et territoires africains en 1999 Source : INED

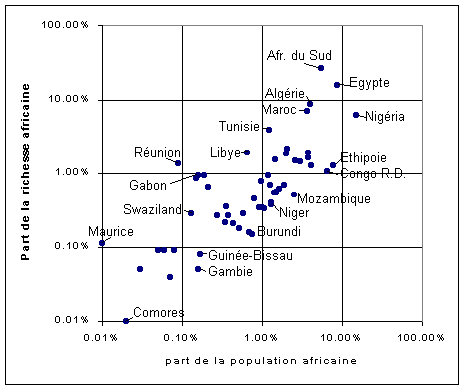
Cliquer ici pour accéder au tableau de données associé.

Utiliser des méthodes de classification adaptées à la problématique (et non pas l'inverse !)

Lorsque l'on a identifié une problématique claire, on peut proposer une classification déductive qui se fondera sur des considérations a priori, indépendantes de la structure des données. Si la problématique retenue est de "Proposer une classification des Etats et territoires africains en fonction de leur poids économique et démographique vers 1999" on peut imaginer une solution du type de celle qui est présentée sur la Figure 4.
 

Figure 4 : Classification des Etats et territoires africains en fonction de leur poids économique et démographique en 1999 Source : INED

On a préféré utiliser une partition ternaire ("petit", "moyen", "grand") plutôt que binaire ("petit", "grand") afin d'éviter l'apparition de groupes de pays trop hétérogènes.  Le choix des seuils (0.5% et 5%) doit être justifié : on a pris comme point de repère le poids théorique moyen des Etats et territoire  africains (56 unités donc 1/56 = 2% environ).  On remarque que certaines classes sont vides (GP, PG) et que la classification finale ne comporte que 7 types au lieu des 9 théoriquement possibles.  Cliquer ici pour accéder au tableau de données associé.

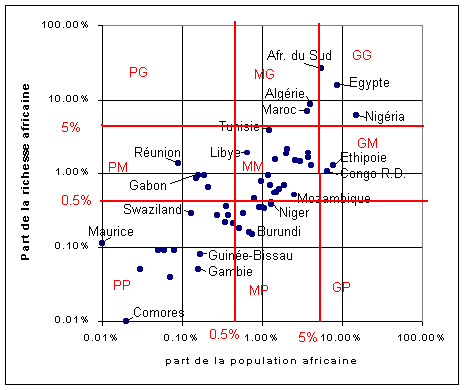
Une problématique différente aurait pu être "Proposez une classification des Etats africains qui tienne compte à la fois de leur taille et de la richesse moyenne de leurs habitants". On aurait alors procédé à un découpage différent sur le modèle de la Figure 5 :
 
 

Figure 5 : Classification des Etats et territoires africains en fonction de leur taille et de la richesse de leurs habitants Source : INED

Les deux diagonales permettent respectivement  de distinguer d'une part les pays "Grands" (A ou B) et "Petits"(C ou D) et d'autre part les pays "Riches" (A ou C) et "Pauvres" (B ou D). Ces notions de taille et de richesse sont évidemment relatives au contexte africain.  Le type A regroupe de grands pays (par la population et/ou la richesse) dont le revenu moyen par habitant est supérieur à la moyenne africaine (ex. Afrique du Sud, Algérie) Le type B regroupe de grands pays (par la population et/ou la richesse) dont le revenu moyen par habitant est inférieur à la moyenne africaine (ex. Nigéria, Ethiopie).  Le type C regroupe des pays petits  (par la population et/ou la richesse) dont le revenu moyen par habitant est supérieur à la moyenne africaine (ex. Gabon, Swaziland) Le type D regroupe des pays petits  (par la population et/ou la richesse) dont le revenu moyen par habitant est inférieur à la moyenne africaine (ex. Gambie, Burundi) Cliquer ici pour accéder au tableau de données associé.

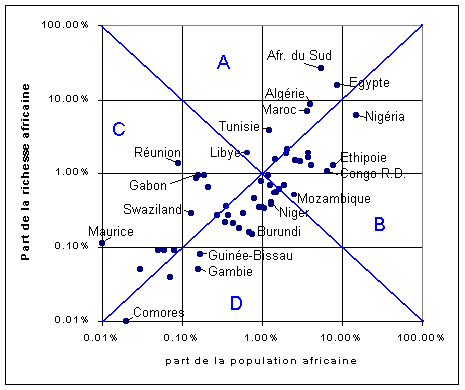
On voit clairement à travers ces deux exemples que le choix de la bonne classification n'est pas un problème statistique qui pourrait être tranché dans l'absolu. La bonne classification est celle qui est en phase avec la problématique retenue.
 

B.3) Combinaison de plusieurs critères

Lorsque l'on doit combiner plus de deux critères, la visualisation de l'information devient difficile sauf dans le cas très particulier d'un tableau de contingence spatial  à trois modalités (diagramme triangulaire) qui sera examiné au cours du chapitre suivant. La typologie doit donc s'appuyer sur d'autres outils d'analyse, même si les principes précédents restent valables (fonder la typologie sur la problématique et non pas l'inverse).

A titre d'exemple, supposons que nous voulions "Etablir une typologie des Etats Africains qui tienne compte à la fois de leur population, de leur richesse et de leur surface exprimées en % du total du continent vers 1999" (Cf. tableau joint).

Construction d'indices synthétiques

Si la problématique consiste à définir un "poids global des Etats africains" qui tienne compte des trois critères disponibles, on peut recourir à la construction d'un indice synthétique qui combine l'ensemble des critères. Différentes méthodes statistiques fondées sur la transformation des variables initiales permettent de réaliser de tels indices. On pourra se reporter pour plus de détail au chapitre 5 de mon cours d'initiation à la statistique descriptive qui montre les différentes solutions disponibles et leur application à un exemple précis.
 

Dans l'exemple proposé, il est inutile de procéder à une transformation des variables puisque les poids des Etats en terme de population, superficie ou richesse sont déjà exprimés sur une échelle commune (% du total africain). Il suffit donc d'établir une moyenne simple ou une moyenne pondérée des critères pour obtenir une valeur globale de magnitude des différents pays.
 

• L'Afrique du Sud qui représente 4% de la superficie, 5.5% de la population et 26.2% du PNB de l'Afrique sera donc créditée d'un poids global de 11.9% si l'on procède à une moyenne simple.
• La R.D. du  Congo (ex-Zaïre) qui totalise 7.7% de la superficie, 6.6% de la population et 1.1.% du PNB de l'Afrique sera quand à elle créditée d'un poids global de 5.1% si l'on applique le même procédé.

Cet exemple permet évidemment d'illustrer les limites de la méthode des indices car il est évident qu'un même poids global peut correspondre à des atouts tout à fait différents. La Tunisie (0.5% superficie / 1.2% population / 3.8% PNB) se retrouve ainsi créditée d'un poids global de 1.9% identique à celui du Tchad (4.2% superficie / 1.0% population / 0.3% PNB) alors que les facteurs mis en jeu sont de nature radicalement différente. Si l'on avait pondéré les critères (e.g. accorder plus de poids à la richesse et moins à la superficie), les deux pays auraient obtenu des scores différents, mais celà ne fait que déplacer le problème dans la mesure ou toute pondération (et l'absence de pondération en est une) peut être critiquée.

Le défaut majeur de la méthode des indices réside dans la tentative de ramener à une seule dimension des réalités qui peuvent être pluridimensionnelles. Chaque fois que l'on se trouve confrontée à des indices synthétiques (IDH, classement des villes européennes, ...) il faut donc être parfaitement conscient des hypothèses très simplificatrices qui ont présidé à leur établissement. Cela ne signifie pas que la méthode des indices soit à bannir, mais elle ne constitue en général qu'une première étape permettant de dégrossir le problème pour dégager un facteur principal de différenciation.

Analyse factorielle (sans recours à des procédures statistiques)

Le terme d'analyse factorielle peut être compris dans un sens conceptuel et non pas purement statistique. Procéder à une analyse factorielle signifie que l'on veut regrouper les variables initiales en un nombre limité de variables plus synthétiques appelées facteur, que l'on cherchera en général à rendre indépendants les uns des autres. Il s'agit donc avant tout d'une simplification et d'une clarification d'une information initiale trop abondante pour être interprétée telle quelle.

Dans l'exemple des Etats africains, on peut considérer que l'indice de taille qui a été établi précédemment constitue le premier facteur de l'analyse et défini la magnitude des Etats, tous critères confondus. Même si ce critère est simplificateur, il permet bel et bien d'établir une hiérarchie entre les Etats africains en fonction de leur poids global.
On doit ensuite lui adjoindre un second facteur qui définit le style de puissance des Etats, c'est-à-dire les critères qui contribuent le plus à l'établissement de leur taille. Il s'agit, si l'on veut, de repérer les atouts ou handicaps des différents Etats, indépendamment de leur taille.

Une manière simple d'établir ce second facteur consiste à diviser chaque variable de taille par la moyenne générale des trois critères et à retenir comme facteurs spécifiques les critères qui sont supérieur de 50% à la moyenne générale.

• L'Afrique du Sud possède ainsi un style de puissance marqué par un poids économique beaucoup plus fort que son poids global  (indice 100*26.2/11.9 = 220). Inversement, son poids démographique (indice 46) et son poids géographiques (indice 34) sont plus faibles que son poids global.
• Le Nigéria possède en revanche un poids démographique supérieur à son poids global (indice 100*14.8/8=185) , et des poids économique (indice 77) et géographique (indice 38) nettement plus faibles.

En combinant les deux facteurs mis en évidence par l'analyse, on peut donc proposer une typologie de la puissance des Etats africains qui tienne compte à la fois de leur magnitude et de leur style (Figure 6).
 

Figure 6 : Puissance relative des Etats africains pour trois critères vers 1999

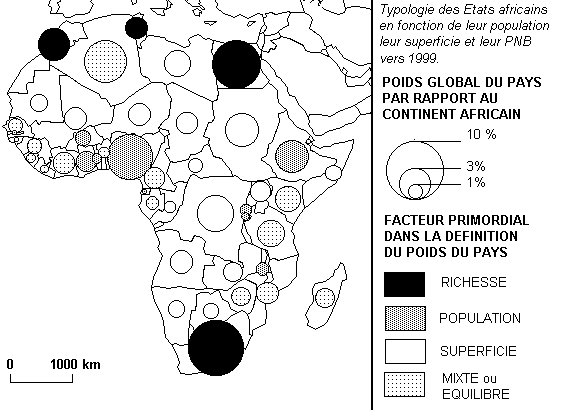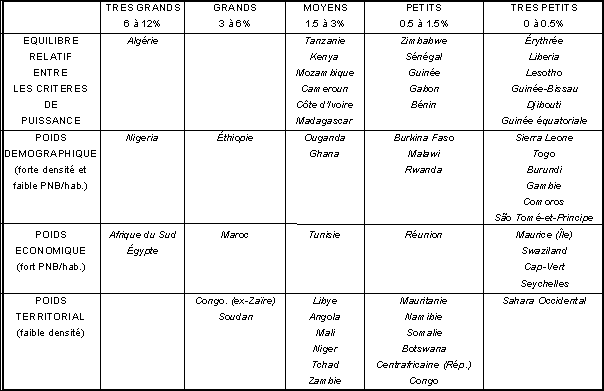Analyse factorielle et classification automatique (avec procédures statistiques)

Bien qu'il ne soit pas possible dans le cadre de cette préparation à l'agrégation de proposer un cours en bonne et due morme sur les méthodes statistiques multivariées, on ne saurait trop recommander aux candidats qui ne maîtrisent pas ces méthodes d'apprendre à en connaître les bases et surtout d'être capable d'interpréter les résultats d'une classification automatique ou d'une analyse factorielle. Il y a en effet tout lieu de penser que certains sujets proposés pourraient se fonder sur l'analyse et l'interprétation des résultats de méthodes multivariées, méthodes que les étudiants de géographie sont supposés connaître à l'issue de la licence. On peut certes envisager des sujets plus "softs" (analyse d'une matrice Bertin) mais les procédures d'analyse et d'interprétation seront de toutes façon les mêmes.

=> Pour les personnes qui ne connaissent pas du tout ces méthodes, le plus simple et le plus efficace est peut-être de partir des chapitres n°18 à 21 de l'ouvrage de E. Blin & J.P. Bord (1993), Initiation géo-graphiques. qui comporte des exercices corrigés.
=> Pour ceux qui ont déjà vu ces méthodes mais souhaitent se raffraîchir la mémoire, utiliser plutôt l'ouvrage de L. Sanders, 1989, L'analyse statistique des données en géographie en étudiant très précisément les exemples d'application qui sont proposés et en essayant de s'entraîner à interpréter seul les résultats.
 

C) CLASSIFICATION & REGIONALISATION
 

C.1) Différence entre classification et régionalisation

La classification des lieux en fonction de leurs degrés de ressemblances peut déboucher dans certains cas sur une forme particulière de régionalisation (régions homogène) mais les deux concepts de régionalisation et de classification doivent être clairement distingués. En effet :
 

• Certains types de régionalisation utilisent des critères autres que la ressemblance des lieux (régions fonctionnelles, régions polarisées) et ne relèvent donc pas du domaine de la classification tel qu'on l'a étudié précédemment.
• Une classification ne débouche pas obligatoirement sur une régionalisation. En effet, les lieux qui appartiennent à la même classe (ressemblance) peuvent être dispersés dans l'espace et n'autorisent pas dans ce cas là l'établissement de régions homogènes. Pour parler de région homogène, il faut rassembler des lieux qui soient à la fois ressemblants et proches spatialement (voire contigus).

L'exercice de commentaire de cartes topographiques a longtemps fourni l'exemple le plus parfait de régonalisation monocritère à travers la délimitation d'entités topographiques (plaines, plateaux, collines, montagnes, buttes, vallées) fondées prioritairement sur l'étude de la distribution des altitudes. Cet exemple permet de saisir parfaitement la différence entre une régionalisation et une classification.
 
 

Figure 7 : Régionalisation fondée sur les niveaux des altitudes

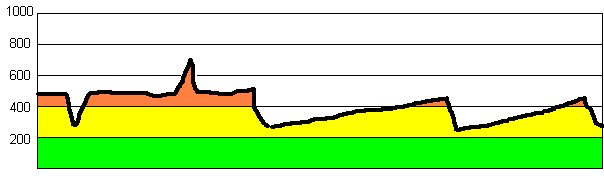Si l'on décide de faire des classes d'altitude (0-200 m) (200-400 m) (400-600m) on voit apparaître 2 types de lieux qui se répartissent entre 8 régions le long de la coupe topographique. On considère en effet que le seuil de 400 m est une limite fondamentale et que l'on change de région chaque fois que ce seuil est franchi.

 

Figure 8 : Régionalisation fondée sur les formes et les discontinuités

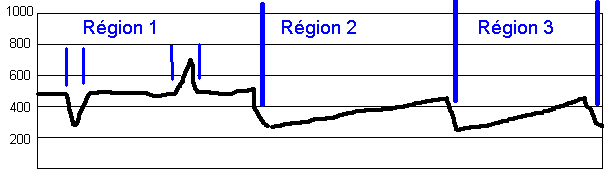Si l'on décide de ne pas s'intéresser aux niveaux absolus d'altitude mais aux niveaux relatifs (pentes), on peut identifier 7 discontinuités topographiques majeures qui définissent a priori autant de régions. On peut toutefois considérer que ces discontinuités ne sont pas de même gabarit spatial et que certaines correspondent à des accidents locaux (vallée, relief postiche) alors que d'autres coïncident à la limite entre des entités topographiques de niveau supérieur.  Dans l'exemple proposé, il semble raisonnable de considérer qu'il existe seulement trois entités topographiques correspondant respectivement à un plateau sub-horizontal et deux topographies inclinées (qui sont sans doute aussi des plateaux mais on ne peut l'affirmer faute de disposer de la preuve de l'encaissement des cours d'eaux.

L'intérêt de ce petit exemple est de montrer l'importance de l'échelle et des discontinuités spatiales dans la définition des régions. D'une part, le nombre de régions varie selon le gabarit implicite qui leur est attribué par lobservateur (élimination des entités de superficie trop petite, subdivision des entités trop vastes). D'autre part, les limites des régions s'appuient davantage sur des variations relatives de l'indicateur (changement brutal de niveau) que sur des variations absolues (franchissement d'un seuil statistique).
On ne peut évidemment pas généraliser ces observations (il existe des cas ou les limites de régions ne peuvent pas s'appuyer sur des discontinuités et correspondent à des zones de transition) mais elles montrent bien que la prise en compte de la dimension spatiale est indispensable si l'on veut établir des entités géographqiues cohérentes.

C.3) Exemple de régionalisation fondée sur l'identification de noyaux homogènes et de discontinuités territoriales.

Si l'on admet que les régions homogènes sont des ensembles d'unités spatiales qui sont à la fois ressemblantes et proches spatialement, on peut proposer des types particulier de cartographie qui permettent de visualiser directement les ressemblances ou les dissemblances. On peut ainsi relier par un trait les régions voisines qui se ressemblent le plus et analyser le graphe associé pour repérer des noyaux homogènes (groupes de régions proches fortement ressemblantes entre elles) et des discontinuités territoriales (limites séparant des groupes d'unités spatiales dissemblantes). Les ressemblances qui sont cartographiées peuvent se fonder sur l'étude simultanée d'un ensemble de critères, à l'instar de l'exemple présenté sur la Figure 9.
 
 

Figure 9 : Similarité des structures par âges des régions d'Europe centrale vers 1980 Source : Grasland C., 1998, " Existe-t-il une Europe Centrale démographique ?", in Rey V. (ed.), Les territoires centre-européens : dilemmes et défis, Lectio-Géographie, La Découverte, Paris, pp. 95-119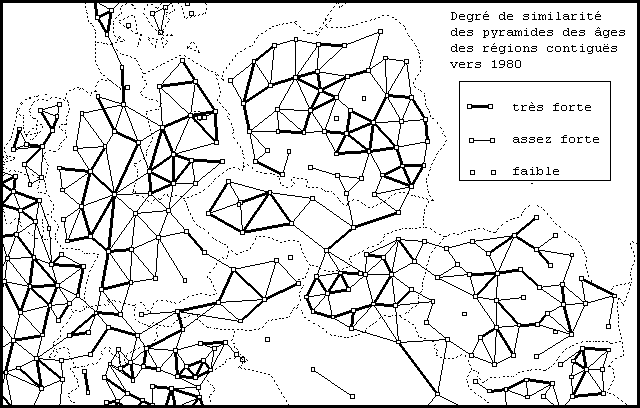

On a relié les régions contiguës dont les pyramides des âges sont les plus ressemblantes, ce qui permet de faire apparaître des groupes de régions qui se ressemblent de proche en proche et, indirectement, de repérer les lignes de discontinuités qui séparent les régions ayant des structures par âge différentes.  On peut ainsi repérer l'influence très frappante des entités étatiques sur la distribution des structures par âge, même si de nombreuses exceptions apparaissent, révélatrices d'autres facteurs historiques, culturels ou linguistiques. La limite entre les deux Allemagnes est ainsi peu marquée, les 30 années de séparation n'ayant pas suffi à différencier des structures par âge qui sont héritières d'événements antérieurs. On remarque également de nombreux cas de transgression des limites politiques, en particulier dans les zones occupées par des minorités culturelles ou linguistiques situées de part et d'autres d'une frontière.

Les méthodes d'analyse des ressemblances dans l'espace renvoient à des méthodes spécifiques d'analyse spatiale (autocorrélation spatiale et autocorrélation territoriale) que l'on ne peut développer ici mais qui sont expliquées de façon plus détaillée dans le chapitre 4 de notre cours d'analyse spatiale de licence.

CONCLUSION

On n'a fait ici qu'aborder de façon superficielle la question de la classification (qui est au centre de toute démarche scientifique) et la question de la régionalisation (qui est au coeur de la démarche géographique). Le candidat à l'agrégation doit être conscient que, parmi les types d'exercices qui peuvent lui être proposés, l'établissement d'une classification ou d'une régionalisation est l'un des sujets les plus intéressants  mais aussi les plus difficiles...
 

A RETENIR :
 

La classification est au coeur de toute démarche scientifique. La classification opère un arbitrage délicat entre simplification et restitution de l'information initiale.  La régionalisation est au coeur de la démarche géographique. Classification et régionalisation sont deux choses différentes. Le choix d'une méthode de classification dépend de la problématique adoptée. Les méthodes factorielles (statistiques ou non) sont plus pertinentes que les méthodes fondées sur des indices synthétiques.

Exercices

EXERCICE N°7
    Exemple de classification fondée sur la méthode de la matrice Bertin
     sujet : Structure par âge des pays du bassin méditerranéen

EXERCICE N°8
    Comparaison de la méthode des indices et de l'analyse statistique multivariée
     sujet : La mesure du développement humain
 
 

Bibliographie
 

Pour une présentation générale des méthodes de classification et leur importance scientifique, on peut se reporter à :

• Chandon J.L., Pinson S., 1981, L'analyse typologique : théorie et applications, Masson, Paris, 254 p.

• Durand-Dastès F., Sanders L. ,1984,  "Les contrastes climatiques : noyaux et zones de transition", in Theo Quant, Géoscopie de la France, Paradigme, Paris, pp. 91-101
• Durand-Dastès  F., 1987, "Une classification des climats de l'Inde", inédit, disponible sur le CD-Rom "Travaux de F. Durand-Dastès".

• Sanders L., 1989, L'analyse statistique des données en géographie, Montpellier, Reclus, Collection Alidade, 268 p.

• Blin E., Bord J.P., 1993, Initiation géo-graphique, Paris, SEDES, 284 p.

Pour l'étude des discontinuités spatiales et des méthodes de régionalisation associées, se reporter à l'article suivant :

• Grasland C., 1997, " L’analyse géographique des discontinuités territoriales : l'exemple de la structure par âge des régions européennes vers 1980 ", Espace Géographique, 4, 30 p.

Pour des exemples d'application de l'analyse multivariée en géographie, on peut se reporter à notre cours de géographie du Monde qui utilise à plusieurs reprises des méthodes d'analyse factorielle pour décrire et classer les pays du Monde. Voir en particulier les chapitres B.1 (taille des états) ,  B.2 (transition démographique)  et  B.3 (indicateurs de développement) qui présentent des interprétations d'analyse factorielle.